La función Totient de Euler Φ (n) para una entrada n es el recuento de números en {1, 2, 3, …, n} que son primos relativos a n, es decir, los números cuyo MCD (máximo común divisor) con n es 1 .
Ejemplos:
Φ(1) = 1 gcd(1, 1) is 1 Φ(2) = 1 gcd(1, 2) is 1, but gcd(2, 2) is 2. Φ(3) = 2 gcd(1, 3) is 1 and gcd(2, 3) is 1 Φ(4) = 2 gcd(1, 4) is 1 and gcd(3, 4) is 1 Φ(5) = 4 gcd(1, 5) is 1, gcd(2, 5) is 1, gcd(3, 5) is 1 and gcd(4, 5) is 1 Φ(6) = 2 gcd(1, 6) is 1 and gcd(5, 6) is 1,
Cómo calcular Φ(n) para una entrada nΦ
Una solución simple es iterar a través de todos los números del 1 al n-1 y contar los números con mcd con n como 1. A continuación se muestra la implementación del método simple para calcular la función Totient de Euler para un entero de entrada n.
C++
// A simple C++ program to calculate
// Euler's Totient Function
#include <iostream>
using namespace std;
// Function to return gcd of a and b
int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate Euler Totient Function
int phi(unsigned int n)
{
unsigned int result = 1;
for (int i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver program to test above function
int main()
{
int n;
for (n = 1; n <= 10; n++)
cout << "phi("<<n<<") = " << phi(n) << endl;
return 0;
}
// This code is contributed by SHUBHAMSINGH10
C
// A simple C program to calculate Euler's Totient Function
#include <stdio.h>
// Function to return gcd of a and b
int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate Euler Totient Function
int phi(unsigned int n)
{
unsigned int result = 1;
for (int i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver program to test above function
int main()
{
int n;
for (n = 1; n <= 10; n++)
printf("phi(%d) = %d\n", n, phi(n));
return 0;
}
Java
// A simple java program to calculate
// Euler's Totient Function
import java.io.*;
class GFG {
// Function to return GCD of a and b
static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate
// Euler Totient Function
static int phi(int n)
{
int result = 1;
for (int i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver code
public static void main(String[] args)
{
int n;
for (n = 1; n <= 10; n++)
System.out.println("phi(" + n + ") = " + phi(n));
}
}
// This code is contributed by sunnusingh
Python3
# A simple Python3 program
# to calculate Euler's
# Totient Function
# Function to return
# gcd of a and b
def gcd(a, b):
if (a == 0):
return b
return gcd(b % a, a)
# A simple method to evaluate
# Euler Totient Function
def phi(n):
result = 1
for i in range(2, n):
if (gcd(i, n) == 1):
result+=1
return result
# Driver Code
for n in range(1, 11):
print("phi(",n,") = ",
phi(n), sep = "")
# This code is contributed
# by Smitha
C#
// A simple C# program to calculate
// Euler's Totient Function
using System;
class GFG {
// Function to return GCD of a and b
static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate
// Euler Totient Function
static int phi(int n)
{
int result = 1;
for (int i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver code
public static void Main()
{
for (int n = 1; n <= 10; n++)
Console.WriteLine("phi(" + n + ") = " + phi(n));
}
}
// This code is contributed by nitin mittal
PHP
<Φphp
// PHP program to calculate
// Euler's Totient Function
// Function to return
// gcd of a and b
function gcd($a, $b)
{
if ($a == 0)
return $b;
return gcd($b % $a, $a);
}
// A simple method to evaluate
// Euler Totient Function
function phi($n)
{
$result = 1;
for ($i = 2; $i < $n; $i++)
if (gcd($i, $n) == 1)
$result++;
return $result;
}
// Driver Code
for ($n = 1; $n <= 10; $n++)
echo "phi(" .$n. ") =" . phi($n)."\n";
// This code is contributed by Sam007
Φ>
Javascript
<script>
// Javascript program to calculate
// Euler's Totient Function
// Function to return
// gcd of a and b
function gcd(a, b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate
// Euler Totient Function
function phi(n)
{
let result = 1;
for (let i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver Code
for (let n = 1; n <= 10; n++)
document.write(`phi(${n}) = ${phi(n)} <br>`);
// This code is contributed by _saurabh_jaiswal
</script>
Producción :
phi(1) = 1 phi(2) = 1 phi(3) = 2 phi(4) = 2 phi(5) = 4 phi(6) = 2 phi(7) = 6 phi(8) = 4 phi(9) = 6 phi(10) = 4
El código anterior llama a la función gcd O(n) veces. La complejidad temporal de la función mcd es O(h) donde “h” es el número de dígitos en un número menor de dos números dados. Por lo tanto, un límite superior en la complejidad temporal de la solución anterior es O(N log N) [CómoΦ puede haber como máximo Log 10 n dígitos en todos los números del 1 al n]
Espacio auxiliar: O(log N)
A continuación se muestra una mejor solución . La idea se basa en la fórmula del producto de Euler, que establece que el valor de las funciones totient está por debajo del producto de los factores primos totales p de n.

La fórmula básicamente dice que el valor de Φ(n) es igual a n multiplicado por el subproducto de (1 – 1/p) para todos los factores primos p de n. Por ejemplo, el valor de Φ(6) = 6 * (1-1/2) * (1 – 1/3) = 2.
Podemos encontrar todos los factores primos usando la idea utilizada en esta publicación.
1) Initialize : result = n
2) Run a loop from 'p' = 2 to sqrt(n), do following for every 'p'.
a) If p divides n, then
Set: result = result * (1.0 - (1.0 / (float) p));
Divide all occurrences of p in n.
3) Return result
A continuación se muestra la implementación de la fórmula del producto de Euler.
C++
// C++ program to calculate Euler's
// Totient Function using Euler's
// product formula
#include <bits/stdc++.h>
using namespace std;
int phi(int n)
{
// Initialize result as n
float result = n;
// Consider all prime factors of n
// and for every prime factor p,
// multiply result with (1 - 1/p)
for(int p = 2; p * p <= n; ++p)
{
// Check if p is a prime factor.
if (n % p == 0)
{
// If yes, then update n and result
while (n % p == 0)
n /= p;
result *= (1.0 - (1.0 / (float)p));
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result *= (1.0 - (1.0 / (float)n));
return (int)result;
}
// Driver code
int main()
{
int n;
for(n = 1; n <= 10; n++)
{
cout << "Phi" << "("
<< n << ")" << " = "
<< phi(n) <<endl;
}
return 0;
}
// This code is contributed by koulick_sadhu
C
// C program to calculate Euler's Totient Function
// using Euler's product formula
#include <stdio.h>
int phi(int n)
{
float result = n; // Initialize result as n
// Consider all prime factors of n and for every prime
// factor p, multiply result with (1 - 1/p)
for (int p = 2; p * p <= n; ++p) {
// Check if p is a prime factor.
if (n % p == 0) {
// If yes, then update n and result
while (n % p == 0)
n /= p;
result *= (1.0 - (1.0 / (float)p));
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result *= (1.0 - (1.0 / (float)n));
return (int)result;
}
// Driver program to test above function
int main()
{
int n;
for (n = 1; n <= 10; n++)
printf("phi(%d) = %d\n", n, phi(n));
return 0;
}
Java
// Java program to calculate Euler's Totient
// Function using Euler's product formula
import java.io.*;
class GFG {
static int phi(int n)
{
// Initialize result as n
float result = n;
// Consider all prime factors of n and for
// every prime factor p, multiply result
// with (1 - 1/p)
for (int p = 2; p * p <= n; ++p) {
// Check if p is a prime factor.
if (n % p == 0) {
// If yes, then update n and result
while (n % p == 0)
n /= p;
result *= (1.0 - (1.0 / (float)p));
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result *= (1.0 - (1.0 / (float)n));
return (int)result;
}
// Driver program to test above function
public static void main(String args[])
{
int n;
for (n = 1; n <= 10; n++)
System.out.println("phi(" + n + ") = " + phi(n));
}
}
// This code is contributed by Nikita Tiwari.
Python3
# Python 3 program to calculate
# Euler's Totient Function
# using Euler's product formula
def phi(n) :
result = n # Initialize result as n
# Consider all prime factors
# of n and for every prime
# factor p, multiply result with (1 - 1 / p)
p = 2
while p * p<= n :
# Check if p is a prime factor.
if n % p == 0 :
# If yes, then update n and result
while n % p == 0 :
n = n // p
result = result * (1.0 - (1.0 / float(p)))
p = p + 1
# If n has a prime factor
# greater than sqrt(n)
# (There can be at-most one
# such prime factor)
if n > 1 :
result = result * (1.0 - (1.0 / float(n)))
return int(result)
# Driver program to test above function
for n in range(1, 11) :
print("phi(", n, ") = ", phi(n))
# This code is contributed
# by Nikita Tiwari.
C#
// C# program to calculate Euler's Totient
// Function using Euler's product formula
using System;
class GFG {
static int phi(int n)
{
// Initialize result as n
float result = n;
// Consider all prime factors
// of n and for every prime
// factor p, multiply result
// with (1 - 1 / p)
for (int p = 2; p * p <= n; ++p)
{
// Check if p is a prime factor.
if (n % p == 0)
{
// If yes, then update
// n and result
while (n % p == 0)
n /= p;
result *= (float)(1.0 - (1.0 / (float)p));
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if (n > 1)
result *= (float)(1.0 - (1.0 / (float)n));
return (int)result;
}
// Driver Code
public static void Main()
{
int n;
for (n = 1; n <= 10; n++)
Console.WriteLine("phi(" + n + ") = " + phi(n));
}
}
// This code is contributed by nitin mittal.
PHP
<Φphp
// PHP program to calculate
// Euler's Totient Function
// using Euler's product formula
function phi($n)
{
// Initialize result as n
$result = $n;
// Consider all prime factors
// of n and for every prime
// factor p, multiply result
// with (1 - 1/p)
for ($p = 2; $p * $p <= $n; ++$p)
{
// Check if p is
// a prime factor.
if ($n % $p == 0)
{
// If yes, then update
// n and result
while ($n % $p == 0)
$n /= $p;
$result *= (1.0 - (1.0 / $p));
}
}
// If n has a prime factor greater
// than sqrt(n) (There can be at-most
// one such prime factor)
if ($n > 1)
$result *= (1.0 - (1.0 / $n));
return intval($result);
}
// Driver Code
for ($n = 1; $n <= 10; $n++)
echo "phi(" .$n. ") =" . phi($n)."\n";
// This code is contributed by Sam007
Φ>
Javascript
// Javascript program to calculate
// Euler's Totient Function
// using Euler's product formula
function phi(n)
{
// Initialize result as n
let result = n;
// Consider all prime factors
// of n and for every prime
// factor p, multiply result
// with (1 - 1/p)
for (let p = 2; p * p <= n; ++p)
{
// Check if p is
// a prime factor.
if (n % p == 0)
{
// If yes, then update
// n and result
while (n % p == 0)
n /= p;
result *= (1.0 - (1.0 / p));
}
}
// If n has a prime factor greater
// than sqrt(n) (There can be at-most
// one such prime factor)
if (n > 1)
result *= (1.0 - (1.0 / n));
return parseInt(result);
}
// Driver Code
for (let n = 1; n <= 10; n++)
document.write(`phi(${n}) = ${phi(n)} <br>`);
// This code is contributed by _saurabh_jaiswal
Producción :
phi(1) = 1 phi(2) = 1 phi(3) = 2 phi(4) = 2 phi(5) = 4 phi(6) = 2 phi(7) = 6 phi(8) = 4 phi(9) = 6 phi(10) = 4
Complejidad temporal: O(√n log n)
Espacio Auxiliar: O(1)
Podemos evitar los cálculos de punto flotante en el método anterior. La idea es contar todos los factores primos y sus múltiplos y restar este conteo de n para obtener el valor de la función totient (los factores primos y los múltiplos de factores primos no tendrán gcd como 1)
1) Initialize result as n
2) Consider every number 'p' (where 'p' varies from 2 to Φn).
If p divides n, then do following
a) Subtract all multiples of p from 1 to n [all multiples of p
will have gcd more than 1 (at least p) with n]
b) Update n by repeatedly dividing it by p.
3) If the reduced n is more than 1, then remove all multiples
of n from result.
A continuación se muestra la implementación del algoritmo anterior.
C++
// C++ program to calculate Euler's
// Totient Function
#include <bits/stdc++.h>
using namespace std;
int phi(int n)
{
// Initialize result as n
int result = n;
// Consider all prime factors of n
// and subtract their multiples
// from result
for(int p = 2; p * p <= n; ++p)
{
// Check if p is a prime factor.
if (n % p == 0)
{
// If yes, then update n and result
while (n % p == 0)
n /= p;
result -= result / p;
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result -= result / n;
return result;
}
// Driver code
int main()
{
int n;
for(n = 1; n <= 10; n++)
{
cout << "Phi" << "("
<< n << ")" << " = "
<< phi(n) << endl;
}
return 0;
}
// This code is contributed by koulick_sadhu
C
// C program to calculate Euler's Totient Function
#include <stdio.h>
int phi(int n)
{
int result = n; // Initialize result as n
// Consider all prime factors of n and subtract their
// multiples from result
for (int p = 2; p * p <= n; ++p) {
// Check if p is a prime factor.
if (n % p == 0) {
// If yes, then update n and result
while (n % p == 0)
n /= p;
result -= result / p;
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result -= result / n;
return result;
}
// Driver program to test above function
int main()
{
int n;
for (n = 1; n <= 10; n++)
printf("phi(%d) = %d\n", n, phi(n));
return 0;
}
Java
// Java program to calculate
// Euler's Totient Function
import java.io.*;
class GFG
{
static int phi(int n)
{
// Initialize result as n
int result = n;
// Consider all prime factors
// of n and subtract their
// multiples from result
for (int p = 2; p * p <= n; ++p)
{
// Check if p is
// a prime factor.
if (n % p == 0)
{
// If yes, then update
// n and result
while (n % p == 0)
n /= p;
result -= result / p;
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if (n > 1)
result -= result / n;
return result;
}
// Driver Code
public static void main (String[] args)
{
int n;
for (n = 1; n <= 10; n++)
System.out.println("phi(" + n +
") = " + phi(n));
}
}
// This code is contributed by ajit
Python3
# Python3 program to calculate
# Euler's Totient Function
def phi(n):
# Initialize result as n
result = n;
# Consider all prime factors
# of n and subtract their
# multiples from result
p = 2;
while(p * p <= n):
# Check if p is a
# prime factor.
if (n % p == 0):
# If yes, then
# update n and result
while (n % p == 0):
n = int(n / p);
result -= int(result / p);
p += 1;
# If n has a prime factor
# greater than sqrt(n)
# (There can be at-most
# one such prime factor)
if (n > 1):
result -= int(result / n);
return result;
# Driver Code
for n in range(1, 11):
print("phi(",n,") =", phi(n));
# This code is contributed
# by mits
C#
// C# program to calculate
// Euler's Totient Function
using System;
class GFG
{
static int phi(int n)
{
// Initialize result as n
int result = n;
// Consider all prime
// factors of n and
// subtract their
// multiples from result
for (int p = 2;
p * p <= n; ++p)
{
// Check if p is
// a prime factor.
if (n % p == 0)
{
// If yes, then update
// n and result
while (n % p == 0)
n /= p;
result -= result / p;
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if (n > 1)
result -= result / n;
return result;
}
// Driver Code
static public void Main ()
{
int n;
for (n = 1; n <= 10; n++)
Console.WriteLine("phi(" + n +
") = " +
phi(n));
}
}
// This code is contributed
// by akt_mit
PHP
<Φphp
// PHP program to calculate
// Euler's Totient Function
function phi($n)
{
// Initialize
// result as n
$result = $n;
// Consider all prime
// factors of n and subtract
// their multiples from result
for ($p = 2;
$p * $p <= $n; ++$p)
{
// Check if p is
// a prime factor.
if ($n % $p == 0)
{
// If yes, then
// update n and result
while ($n % $p == 0)
$n = (int)$n / $p;
$result -= (int)$result / $p;
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if ($n > 1)
$result -= (int)$result / $n;
return $result;
}
// Driver Code
for ($n = 1; $n <= 10; $n++)
echo "phi(", $n,") =",
phi($n), "\n";
// This code is contributed
// by ajit
Φ>
Javascript
// Javascript program to calculate
// Euler's Totient Function
function phi(n)
{
// Initialize
// result as n
let result = n;
// Consider all prime
// factors of n and subtract
// their multiples from result
for (let p = 2;
p * p <= n; ++p)
{
// Check if p is
// a prime factor.
if (n % p == 0)
{
// If yes, then
// update n and result
while (n % p == 0)
n = parseInt(n / p);
result -= parseInt(result / p);
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if (n > 1)
result -= parseInt(result / n);
return result;
}
// Driver Code
for (let n = 1; n <= 10; n++)
document.write(`phi(${n}) = ${phi(n)} <br>`);
// This code is contributed
// by _saurabh_jaiswal
Producción :
phi(1) = 1 phi(2) = 1 phi(3) = 2 phi(4) = 2 phi(5) = 4 phi(6) = 2 phi(7) = 6 phi(8) = 4 phi(9) = 6 phi(10) = 4
Complejidad temporal: O(√n log n)
Espacio Auxiliar: O(1)
Tomemos un ejemplo para entender el algoritmo anterior.
n = 10. Initialize: result = 10 2 is a prime factor, so n = n/i = 5, result = 5 3 is not a prime factor. The for loop stops after 3 as 4*4 is not less than or equal to 10. After for loop, result = 5, n = 5 Since n > 1, result = result - result/n = 4
Algunas propiedades interesantes de la función totient de Euler
1) Para un número primo p , ![]()
Prueba :
, where p is any prime numberWe know that
where k is any random number and
[Tex]\\[/Tex]Total number from 1 to p = p Number for which
is
, i.e the number p itself, so subtracting 1 from p
Ejemplos:
[Tex]\\[/Tex]
[Tex]\\[/Tex]
2) Para dos números primos a y b![]() , utilizados en el algoritmo RSA
, utilizados en el algoritmo RSA
Prueba :
, where a and b are prime numbers
,
[Tex]\\[/Tex]Total number from 1 to ab = ab Total multiples of a from 1 to ab =
=
Total multiples of b from 1 to ab =
=
Example:a = 5, b = 7, ab = 35Multiples of a =
= 7 {5, 10, 15, 20, 25, 30, 35}Multiples of b =
= 5 {7, 14, 21, 28, 35}
Can there be any double counting ?(watch above example carefully, try with other prime numbers also for more grasp)Ofcourse, we have counted
twice in multiples of a and multiples of b so, Total multiples = a + b - 1 (with which
with
)
[Tex]\phi(ab) = ab - (a + b - 1)[/Tex] , removing all number with
with
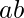
[Tex]\phi(ab) = (a - 1) \cdot (b - 1)[/Tex]
Ejemplos:
[Tex]\\[/Tex]
[Tex]\\[/Tex]
3) Para un número primo p , ![]()
Prueba :
, where p is a prime number
Total numbers from 1 to
Total multiples of
Removing these multiples as with them
[Tex]\\[/Tex]Example : p = 2, k = 5,
= 32Multiples of 2 (as with them
) = 32 / 2 = 16 {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32}
[Tex]\phi(p ^ k) = p ^ k - p ^ {k - 1}[/Tex]
Ejemplos:
[Tex]\\[/Tex]
[Tex]\\[/Tex]
4) Para dos números a y b ![]()
![]()
![]()
Caso especial: mcd(a, b) = 1
![]()
Ejemplos:
Special Case :,
[Tex]\\[/Tex]
[Tex]\\[/Tex]
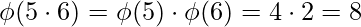
[Tex]\\[/Tex]Normal Case :
,
[Tex]\\[/Tex]
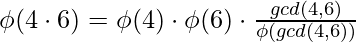
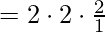
[Tex]\\[/Tex]
[Tex]\\[/Tex]
5) La suma de los valores de las funciones totient de todos los divisores de n es igual a n.

Ejemplos:
n = 6
factors = {1, 2, 3, 6}
n = 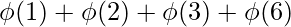 = 1 + 1 + 2 + 2 = 6
= 1 + 1 + 2 + 2 = 6 n = 8factors = {1, 2, 4, 8}n =
n = 8factors = {1, 2, 4, 8}n = 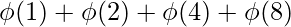 = 1 + 1 + 2 + 4 = 8
= 1 + 1 + 2 + 4 = 8 n = 10factors = {1, 2, 5, 10}n =
n = 10factors = {1, 2, 5, 10}n = 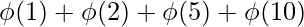 = 1 + 1 + 4 + 4 = 10
= 1 + 1 + 4 + 4 = 10
6) La característica más famosa e importante se expresa en el teorema de Euler :
The theorem states that if n and a are coprime (or relatively prime) positive integers, then aΦ(n) ≡ 1 (mod n)
El criptosistema RSA se basa en este teorema:
En el caso particular cuando m es primo, digamos p, el teorema de Euler se convierte en el llamado pequeño teorema de Fermat :
ap-1 ≡ 1 (mod p)
7) El número de generadores de un grupo cíclico finito bajo la adición de módulo n es Φ(n) .
Artículo relacionado:
Función Totient de Euler para todos los números menores o iguales a n
Función Totient de Euler optimizada para evaluaciones múltiples
Referencias:
http://e-maxx.ru/algo/euler_function
http://en.wikipedia.org/wiki/Euler%27s_totient_function
https://cp-algorithms.com/algebra/phi-function.html
http://mathcenter.oxford.memory.edu/site/math125/chineseRemainderTheorem/
Este artículo es una contribución de Ankur . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA