Funciones definidas por integrales

Al pensar en funciones, siempre imaginamos que una función es una máquina matemática que nos da una salida para cualquier entrada que le demos. Por lo general, se piensa en términos de expresiones matemáticas como cuadrados, funciones exponenciales y trigonométricas, etc. También es posible definir las funciones en términos de integrales definidas. Estas son similares a las funciones de área, que nos permiten calcular el área bajo cualquier curva dados los límites de la integral definida. Veamos cómo definirlos y sus propiedades en detalle.

Funciones definidas por integrales definidas

Se pueden definir nuevas funciones con la ayuda de integrales. Digamos que nos dan una función f(x), entonces la función de área se define como la integral de la función dada dentro de algunos límites. Dado que hay límites dentro de los cuales tenemos que calcular el área, tenemos que usar integrales definidas para definir tales funciones. Entonces, las funciones definidas por integrales se dan como,

F(x) = $\int^{x}_{a} f(x)dx$

Tomemos un ejemplo de tal función, supongamos

f(x) = $\sqrt{x^2 - a^2}$ si 0 ≤ x ≤ 5

La gráfica de la función se verá más o menos así,

Nuestro objetivo es encontrar la función que da el área bajo esta curva. Para un valor particular dado «x», calculamos la integral de 0 a x.

F(x) = $\int^{x}_{0}\sqrt{t^2 - a^2}dt$

¿Qué significa esta función? Dado que esta función es el área bajo la gráfica de f, F(x) es básicamente el área bajo la curva de t = 0 a t = x. La siguiente figura representa esta función de área de t = 0 a t = x.

Propiedades generales de tales funciones.

Estas propiedades nos permiten dibujar la gráfica de tales funciones o simplificar el cálculo en los casos en que no es fácil calcular las expresiones de las funciones:

La función F(x) es continua donde está definida. Esta propiedad proviene del teorema fundamental del cálculo.

En x = a, valor de la función F(a) = 0. Esta propiedad proviene de las propiedades de la integral definida.

F'(x) = f(x).

F”(x) = f'(x)

Si a =0 y f(x) es par, entonces F(x) es impar.

Si f(x) es impar, entonces F(x) es par.

Logaritmo natural

El logaritmo natural es un ejemplo de las funciones que se definen como funciones de las integrales. Para x > 0, el logaritmo natural se define como,

$ln(x) = \int^x_1\frac{1}{x}dx$

Podemos dibujar su curva usando las propiedades mencionadas anteriormente, calculando la intersección x.

F(x) = ln(x) = 0 = $\int^x_1\frac{1}{x}dx$

Esta expresión será cero en x = 1. Por lo tanto, ln(x) = 0 en x = 1.

F'(x) = $\frac{1}{x}$ , F”(x) = $\frac{-1}{x^2}$

Dado que F'(x) siempre es mayor que cero para todos los valores positivos de la entrada, la función siempre es creciente. Note que con una lógica similar, podemos decir F”(x) < 0 para todos los valores de x mayores que cero.

Función de error

Para todos los valores reales de x, la función de error está definida por,

$erf(x) = \frac{2}{\sqrt{\pi}}\int^{x}_{0}e^{-t^2}dt$

Dibujemos un gráfico para esta función también,

Su intercepción en x se da en erf(x) = 0, que es en x =0. Así, la gráfica de esta función pasa por el origen.

F(0) = 0, F'(x) = $\frac{2}{\sqrt{\pi}}e^{-x^2}$ , F”(x) = $\frac{-4x}{\sqrt{\pi}}e^{-x^2}$

F(x) será impar ya que} $\frac{2}{\sqrt{\pi}}e^{-x^2}$ es par. La gráfica de esta función se ve así,

Problemas de muestra

Pregunta 1: Dado F(x) = $\int^{x}_{0}f(t)dt$ . Demuestre que F'(x) = f(x) y F”(x) = f'(x).

Solución:

F(x) = $\int^{x}_{0}f(t)dt$

⇒ F'(x) = f(x)

Diferenciándolo de nuevo,

F”(x) = f'(x)

Pregunta 2: Dada la F(x) = $\int^{x}_{0}t^2dt$ . Encuentre el valor de F(2).

Solución:

F(x) = $\int^{x}_{0}t^2dt$ .

en x = 2

F(x) = $\int^{2}_{0}t^2dt$

⇒ F(x) = $[\frac{t^3}{3}]^{2}_{0}$

⇒ F(x) = $[\frac{2^3}{3} - 0]$

⇒ F(x) = $\frac{8}{3}$

Pregunta 3: Dada la F(x) = $\int^{x}_{0}tdt$ . Encuentre el valor de F(4).

Solución:

F(x) = $\int^{x}_{0}tdt$ .

en x = 4

F(4) = $\int^{4}_{0}tdt$

⇒ F(4) = $[\frac{t^2}{2}]^{4}_{0}$

⇒ F(4) = $[\frac{4^2}{2} - 0]$

⇒ F(4) = 8

Pregunta 4: Encuentra el valor de la función dada g(x) en x = 3.

f(x) = 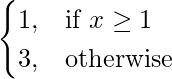$\begin{cases} 1,& \text{if } x\geq 1\\ 3, & \text{otherwise} \end{cases}$

g(x) = $\int^{x}_{0}f(t)dt$

Solución:

La gráfica de la función f(x) viene dada por

Necesitamos calcular el valor de g(x) = $\int^{x}_{0}f(t)dt$

g(3) = $\int^{3}_{0}f(t)dt$

⇒g(3)= $\int^{1}_{0}f(t)dt + \int^{3}_{1}f(t)dt$

⇒g(3) = $\int^{1}_{0}3dt + \int^{3}_{1}1dt$

⇒g(3) = $[3t]^1_0 + [t]^{3}_{1}$

⇒ g(3) = 3 + 1

⇒ g(3) = 4

Pregunta 5: Encuentra el valor de la función dada en x = 1.

f(x) = 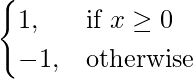$\begin{cases} 1,& \text{if } x\geq 0\\ -1, & \text{otherwise} \end{cases}$

g(x) = $\int^{x}_{-1}f(x)dx$

Solución:

La gráfica de la función f(x) viene dada por

Necesitamos calcular el valor de g(x) = $\int^{x}_{-1}f(t)dt$

g(1) = $\int^{1}_{-1}f(t)dt$

⇒g(1)= $|\int^{0}_{-1}f(t)dt|+ \int^{1}_{0}f(t)dt$

⇒g(1) = $|\int^{0}_{-1}-1dt|+ \int^{1}_{0}1dt$

⇒g(1) = $1 + 1$

⇒g(1) =2

Pregunta 6: Calcula el valor de la función dada f(x) en x = 1.

f(x) = $\int ln(x)$

Solución:

Esta integración se puede resolver aplicando la fórmula por partes para la integración.

Lo sabemos $\frac{d(ln(x))}{dx} = \frac{1}{x}$

Aplicando la integración por partes a la integral

f(x) = $xln(x) - \int1dx$

⇒f(x) = $xln(x) - x$

f(1) = -1

Pregunta 7: Calcula el valor de la función dada f(x) en x = 5.

f(x) = $\int ln(x)$

Solución:

Esta integración se puede resolver aplicando la fórmula por partes para la integración.

Lo sabemos $\frac{d(ln(x))}{dx} = \frac{1}{x}$

Aplicando la integración por partes a la integral

f(x) = $xln(x) - \int1dx$

⇒f(x) = $xln(x) - x$

f(1) = -1

Pregunta 8: Calcula el valor de la función dada x = 2,

g(x) = f(x) + f(-x)

Donde f(x) = $\frac{2}{\sqrt{\pi}}\int^{x}_{0}e^{-t^2}dt$

Solución:

g(x) = f(x) + f(-x)

Sabemos que f(x) es la función de error.

Ahora por las propiedades mencionadas anteriormente, ya que $e^{-t^2}$ es una función par. La función integral debe ser una función impar.

Es decir, f(x) = $\frac{2}{\sqrt{\pi}}\int^{x}_{0}e^{-t^2}dt$ es una función impar.

Como f(x) es una función impar, f(-x) = -f(x).

g(x) = f(x) + f(-x)

⇒ g(x) = f(x) – f(x)

⇒ g(x)= 0

Así, g(2) = 0

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA