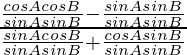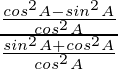La trigonometría es una rama de las matemáticas que se ocupa de los ángulos, las longitudes y las alturas de los triángulos y sus relaciones. Había jugado un papel importante para calcular funciones complejas o grandes distancias que no eran posibles de calcular sin trigonometría. Al resolver problemas de trigonometría, nos encontramos con muchas situaciones en las que tenemos que calcular las soluciones trigonométricas para la suma de ángulos o la diferencia de ángulos. P.ej

Aquí, ![]()
Que es una razón trigonométrica tangente, con un ángulo opuesto a BC.
tan(θ+Φ) = ![]()
Si θ = 30° y Φ = 45°. Conocemos los ángulos trigonométricos de 45° y 30°, pero no conocemos el ángulo trigonométrico de (45° + 30° = 75°). Entonces, para simplificar este tipo de problemas. Aprenderemos fórmulas trigonométricas o identidades de suma y diferencia de dos ángulos que facilitarán las cosas.
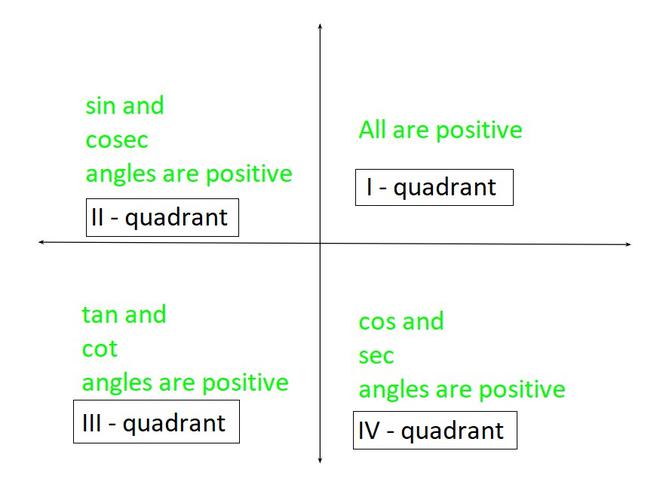
Antes de continuar, primero veremos los signos de las funciones trigonométricas en los cuatro cuadrantes. Estos signos juegan un papel importante en la trigonometría.
Identidades trigonométricas
Ahora vamos a encontrar las identidades trigonométricas. Como sabemos que
sen(-x) = – sen x
cos(-x) = cos x
Porque solo cos y sec son positivos en el cuarto cuadrante. Entonces, ahora probamos algunos resultados con respecto a la suma y diferencia de ángulos:
Consideremos un círculo unitario (que tiene un radio de 1) con centro en el origen. Sea x el ∠DOA y sea y el ∠AOB. Entonces (x + y) es el ∠DOB. También sea (– y) el ∠DOC.
Por lo tanto, las coordenadas de A, B, C y D son
A = (cos x, sen x)
B = [cos (x + y), sen (x + y)]
C = [cos (– y), sen (– y)]
D = (1, 0).
Como, ∠AOB = ∠COD
Sumando, ∠BOC en ambos lados, obtenemos
∠AOB + ∠BOC = ∠COD + ∠BOC
∠COA = ∠BOD
En △ AOC y △ BOD
OA = OB (radio del círculo)
∠AOC = ∠BOD (Probado anteriormente)
OC = OD (radio del círculo)
△ AOC ≅ △ BOD por congruencia SAS.
Usando la fórmula de la distancia, para
AC 2 = [cos x – cos (– y)] 2 + [sen x – sin(–y] 2
AC 2 = 2 – 2 (cos x cos y – sen x sen y) …………….(i)
Y ahora
De manera similar, usando la fórmula de la distancia, obtenemos
BD 2 = [1 – cos (x + y)] 2 + [0 – sen (x + y)] 2
BD 2 = 2 – 2 cos (x + y) …………….(ii)
Como, △ AOC ≅ △ DBO
AC = BD, entonces AC 2 = BD 2
De eq(i) y eq(ii), obtenemos
2 – 2 (cos x cos y – sen x sen y) = 2 – 2 cos (x + y)
Asi que,
cos (x + y) = cos x cos y – sen x sen y
Toma y = -y, obtenemos
cos (x + (-y)) = cos x cos (-y) – sen x sen (-y)
cos (x – y) = cos x cos y + sen x sen y
Ahora, tomando
cos (
-(x + y)) = cos ((
-x) – y) (cos (
-θ) = sen θ)
sen (x – y) = sen x cos y – cos x sen y
toma y = -y, obtenemos
sen (x – (-y)) = sen x cos (-y) – cos x sen (-y)
sen (x + y) = sen x cos y + cos x sen y
Las fórmulas derivadas de razones trigonométricas de ángulos compuestos son las siguientes:
sen (A + B) = sen A cos B + cos A sen B ………………..(1)
sen (A – B) = sen A cos B – cos A sen B ………………..(2)
cos (A + B) = cos A cos B – sen A sen B .. ………………(3)
cos (A – B) = cos A cos B + sen A sen B ………………..(4)
Al usar estas fórmulas, podemos obtener una forma importante y más utilizada:
(1) Tomar, A = ![]()
En la ecuación (1) y (3), obtenemos
sen (
+B) = cos B
cos (
+B) = – sen A
(2) Tome, A = π
En la ecuación (1), (2), (3) y (4) obtenemos
sen (π + B) = – sen B
sen (π – B) = sen B
coseno (π ± B) = – coseno B
(3) Tome, A = 2π
En la ecuación (2) y (4) obtenemos
sen (2π – B) = – sen B
coseno (2π – B) = coseno B
De manera similar para cot A, tan A, sec A y cosec A
(4) ![]()
Aquí, A, B y (A + B) no son un múltiplo impar de π/2, por lo tanto, cosA, cosB y cos(A + B) no son cero
tan(A + B) = sen(A + B)/cos(A + B)
De la ecuación (1) y (3), obtenemos
tan(A + B) = sen A cos B + cos A sen B/cos A cos B – sen A sen B
Ahora dividimos el numerador y el denominador por cos A cos B obtenemos
tan(A + B) =
(5) ![]()
Como sabemos que
Entonces, al poner B = -B, obtenemos
(6) ![]()
Aquí, A, B y (A + B) no son múltiplos de π, por lo tanto, sinA, sinB y sin(A + B) no son cero
cot(A + B) = cos(A + B)/sen(A + B)
De la ecuación (1) y (3), obtenemos
cot(A + B) = cos A cos B – sen A sen B/sen A cos B + cos A sen B
Ahora dividimos el numerador y el denominador por sen A sen B obtenemos
cuna(A + B) =
(7) ![]()
Como sabemos que
Entonces, al poner B = -B, obtenemos
Aquí, estableceremos dos conjuntos de fórmulas de transformación: fórmulas de factorización y desfactorización.
Fórmulas de desfactorización
En trigonometría, la desfactorización significa convertir un producto en una suma o diferencia. Las fórmulas de desfactorización son:
(1) 2 sen A cos B = sen (A + B) + sen (A – B)
Prueba:
Como sabemos que
sen (A + B) = sen A cos B + cos A sen B ………………………(1)
sen (A – B) = sen A cos B – cos A sen B ………………………(2)
Sumando las ecuaciones (1) y (2), obtenemos
2 sen A cos B = sen (A + B) + sen (A – B)
(2) 2 cos A sen B = sen (A + B) – sen (A – B)
Prueba:
Como sabemos que
sen (A + B) = sen A cos B + cos A sen B ………………………(1)
sen (A – B) = sen A cos B – cos A sen B ………………………(2)
Restando la ecuación (2) de (1), obtenemos
2 porque A sen B = sen (A + B) – sen (A – B)
(3) 2 cos A cos B = cos (A + B) + cos (A – B)
Prueba:
Como sabemos que
cos (A + B) = cos A cos B – sen A sen B ………………………(1)
cos (A – B) = cos A cos B + sen A sen B ………………………(2)
Sumando las ecuaciones (1) y (2), obtenemos
2 cos A cos B = cos (A + B) + cos (A – B)
(4) 2 sen A sen B = cos (A – B) – cos (A + B)
Prueba:
cos (A + B) = cos A cos B – sen A sen B ………………………(1)
cos (A – B) = cos A cos B + sen A sen B ………………………(2)
Restando la ecuación (3) de (4), obtenemos
2 sen A sen B = cos (A – B) – cos (A + B)
Ejemplo 1. Convierte cada uno de los siguientes productos en la suma o diferencia.
(i) 2 sen 40° cos 30°
(ii) 2 sen 75° sen 15°
(iii) cos 75° cos 15°
Solución:
(i) Dado: A = 40° y B = 30°
Ahora pon todos estos valores en la fórmula,
2 sen A cos B = sen (A + B) + sen (A – B)
Obtenemos
2 sen 40° cos 30° = sen (40 + 30) + sen (40 – 30)
= pecado (70°) + pecado (10°)
(ii) Dado: A = 75° y B = 15°
Ahora pon todos estos valores en la fórmula,
2 sen A sen B = cos (A – B) – cos (A + B)
Obtenemos
2 sen 75° sen 15° = coseno (75-15) – coseno (75+15)
= coseno (60°) – coseno (90°)
(iii) Dado: A = 75° y B = 15°
Ahora pon todos estos valores en la fórmula,
2 cos A cos B = cos (A + B) + cos (A – B)
Obtenemos
cos 75° cos 15° = 1/2(cos (75+15) + cos (75-15))
= 1/2 (cos (90°) + cos (60°))
Ejemplo 2. Resolver para ![]()
Solución:
Usando la fórmula
2 cos A cos B = cos (A + B) + cos (A – B)

=
=
=
Por eso,
= 0
Fórmulas de factorización
En trigonometría, la factorización significa convertir la suma o la diferencia en el producto. Las fórmulas de factorización son:
(1) sen (C) + sen (D) = 2 sen ![]() cos
cos ![]()
Prueba:
Tenemos
2 sen A cos B = sen (A + B) + sen (A – B) ………………………(1)
Así que ahora, estamos tomando
A + B = C y A – B = D
Entonces, A =
y B =
Ahora ponga todos estos valores en la ecuación (1), obtenemos
2 sen (
) cos (
) = sen (C) + sen (D)
O
sen (C) + sen (D) = 2 sen (
) cos (
)
(2) sen (C) – sen (D) = 2 cos ![]() sen
sen ![]()
Prueba:
Tenemos
2 porque A sen B = sen (A + B) – sen (A – B) ………………………(1)
Así que ahora, estamos tomando
A + B = C y A – B = D
Entonces, A =
y B =
Ahora ponga todos estos valores en la ecuación (1), obtenemos
2 cos (
) sen (
) = sen (C) – sen (D)
O
sen (C) – sen (D) = 2 cos (
) sen (
)
(3) cos (C) + cos (D) = 2 cos ![]() cos
cos ![]()
Prueba:
Tenemos
2 cos A cos B = cos (A + B) + cos (A – B) ………………………(1)
Así que ahora, estamos tomando
A + B = C y A – B = D
Entonces, A =
y B =
Ahora ponga todos estos valores en la ecuación (1), obtenemos
2 coseno (
) coseno (
) = coseno (C) + coseno (D)
O
coseno (C) + coseno (D) = 2 coseno (
) coseno (
)
(4) cos (C) – cos (D) = 2 sen ![]() sen
sen ![]()
Prueba:
Tenemos
2 sen A sen B = cos (A – B) – cos (A + B) ………………………(1)
Así que ahora, estamos tomando
A + B = C y A – B = D
Entonces, A =
y B =
Ahora ponga todos estos valores en la ecuación (1), obtenemos
2 sen (
) sen (
) = cos (C) – cos (D)
O
cos (C) – cos (D) = 2 sen (
) sen (
)
Explique 1. Exprese cada uno de los siguientes como un producto
(i) sen 40° + sen 20°
(ii) sen 60° – sen 20°
(iii) cos 40° + cos 80°
Solución:
(i) Dado: C = 40° y D = 20°
Ahora pon todos estos valores en la fórmula,
sen (C) + sen (D) = 2 sen
cos
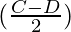
Obtenemos
sen 40° + sen 20° = 2 sen
cos
= 2 seno
cos
= 2 sen 30° cos 10°
(ii) Dado: C = 60° y D = 20°
Ahora pon todos estos valores en la fórmula,
sen (C) – sen (D) = 2 cos
sen
Obtenemos
sen 60° – sen 20° = 2 cos
sen
= 2
coseno
= 2 cos 40° sen 20°
(iii) Dado: C = 80° y D = 40°
Ahora pon todos estos valores en la fórmula,
cos (C) + cos (D) = 2 cos
cos
Obtenemos
cos 40° + cos 80° = 2 cos
cos
= 2 porque
porque
= 2 cos 60° cos 20°
Ejemplo 2. Demostrar que: 1 + cos 2x + cos 4x + cos 6x = 4 cos x cos 2x cos 3x
Solución:
Tomemos LHS
1 + cos 2x + cos 4x + cos 6x
Aquí, cos 0x = 1
Asi que,
(cos 0x + cos 2x) + (cos 4x + cos 6x)
Usando fórmula
cos (C) + cos (D) = 2 cos
cos
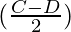
Obtenemos
(2 cos
cos
) + (2 cos
cos
)
(2 cos x cos x) + (2 cos 5x cos x)
Tomando 2 cos x común, tenemos
2 cos x (cos x + cos 5x)
Nuevamente usando la fórmula
cos (C) + cos (D) = 2 cos
cos
Obtenemos
2 cos x (2 cos
cos
)
2 cos x (2 cos 3x cos 2x)
4 cos x cos 2x cos 3x
LHS = RHS
Por lo tanto probado
Razones trigonométricas de múltiples ángulos (2A) en términos del ángulo A
Las razones trigonométricas de un ángulo en un triángulo rectángulo definen la relación entre el ángulo y la longitud de sus lados. sen 2x o cos 2x, etc. también son una de esas fórmulas trigonométricas, también conocida como fórmula de ángulo doble, ya que tiene un ángulo doble.
(1) sen 2A = 2 sen A cos A
Prueba:
Como sabemos que
sen (A + B) = sen A cos B + cos A sen B ………………..(1)
Ahora tomando B = A, en la ecuación (1), obtenemos
sen (A + A) = sen A cos A + cos A sen A
sen 2A = 2 sen A cos A
(2) cos 2A = cos 2 A – sen 2 A
Prueba:
Como sabemos que
cos (A + B) = cos A cos B – sen A sen B ………………..(1)
Ahora tomando B = A, en la ecuación (1), obtenemos
cos (A + A) = cos A cos A + sen A sen A
cos 2A = cos 2 A – sen 2 A
(3) cos 2A = 2 cos 2 A – 1
Prueba:
Como sabemos que
cos 2A = cos 2 A – sen 2 A ………………..(1)
También sabemos que
sen 2 A + cos 2 A = 1
Entonces, sen 2 A = 1 – cos 2 A
Ahora pon el valor de sen 2 A en la ecuación (1), obtenemos
cos 2A = cos 2 A – (1 – cos 2 A)
cos 2A = cos 2 A – 1 + cos 2 A
cos 2A = 2 cos 2 A – 1
(4) cos 2A = 1 – 2sen 2 A
Prueba:
Como sabemos que
cos2A = 2cos2A – 1 ………………..(1)
También sabemos que
sen 2 A + cos 2 A = 1
Entonces, cos 2 A = 1 – sen 2 A
Ahora pon el valor de sen 2 A en la ecuación (1), obtenemos
cos 2A = 2(1 – sen 2 A) – 1
cos 2A = 2 – 2sen 2 A) – 1
cos 2A = 1 – 2sen 2 A
(5) cos 2A = ![]()
Prueba:
Como sabemos que
cos 2A = cos 2 A – sen 2 A
Entonces, ahora dividiendo, por sen 2 A + cos 2 A = 1, obtenemos
cos 2A =
Nuevamente dividiendo el numerador y el denominador por cos 2 A, obtenemos
cos 2A =
cos 2A =
(6) sen 2A = ![]()
Prueba:
Como sabemos que
sen (A + B) = sen A cos B + cos A sen B ………………..(1)
Ahora tomando B = A, en la ecuación (1), obtenemos
sen (A + A) = sen A cos A + cos A sen A
sen 2A = 2 sen A cos A
Como también sabemos que sen 2 A + cos 2 A = 1
Entonces, ahora dividiendo, por sen 2 A + cos 2 A = 1, obtenemos
sen 2A =
Ahora, al dividir el numerador y el denominador por cos 2 A, obtenemos
sen 2A =
(7) tan 2A = ![]()
Prueba:
Como sabemos que
………………..(1)
Ahora tomando B = A, en la ecuación (1), obtenemos
tan(A + A) =
bronceado 2A =
Ejemplo: probar que
(i) ![]() = tan θ
= tan θ
(ii) ![]() = cuna θ
= cuna θ
(iii) cos 4x = 1 – 8 sen 2 x cos 2 x
Solución:
(i) sen 2θ = 2 sen θ cos θ ………..(de la identidad 1)
y, 1 + cos 2θ = 2 cos 2 θ ………..(de la identidad 3)
=
= bronceado θ
Por lo tanto probado
(ii) sen 2θ = 2 sen θ cos θ ………..(de la identidad 1)
y, 1 – cos 2θ = 2sen 2 θ ………..(de la identidad 4)
=
= cuna θ
Por lo tanto probado
(iii) cos 4x = cos 2(2x)
= 1 – 2sen 2 (2x) (usando 16)
= 1 – 2(sen(2x)) 2
= 1 – 2(2 sen x cos x) 2 (usando la identidad 1)
= 1 – 2(4 sen 2 x cos 2 x)
cos 4x = 1 – 8 sen 2 x cos 2 x
Por lo tanto probado
Razones trigonométricas de múltiples ángulos (3A) en términos del ángulo A
Las razones trigonométricas de un ángulo en un triángulo rectángulo definen la relación entre el ángulo y la longitud de sus lados. sen 3x o cos 3x, etc. también son una de esas fórmulas trigonométricas, también conocida como fórmula de ángulo triple, ya que tiene un ángulo triple.
(1) sen 3A = 3 sen A – 4 sen 3 A
Prueba:
Tomemos LHS
sen 3A = sen (2A + A)
Usando la identidad
sen (A + B) = sen A cos B + cos A sen B
Obtenemos
sen 3A = sen 2A cos A + cos 2A sen A
= 2sen A cos A cos A + (1 – 2sen 2 A)sen A
= 2sen A(1 – sen 2 A) + sen A – 2sen 3 A
= 2 sen A – 2 sen 3 A + sen A – 2 sen 3 A
sen 3A = 3 sen A – 4 sen 3 A
(2) cos 3A = 4 cos 3 A – 3 cos A
Prueba:
Tomemos LHS
sen 3A = sen (2A + A)
Usando la identidad
cos (A + B) = cos A cos B – sen A sen B
Obtenemos
cos 3A = cos 2A cos A – sen 2A sen A
= (2 cos 2 A – 1) cos A – 2 sen A cos A sen A
= (2cos 2 A – 1)cos A – 2cos A(1 – cos 2 A)
= 2 cos 3 A – cos A – 2 cos A + 2 cos 3 A)
cos 3A = 4 cos 3 A – 3 cos A
(3) bronceado 3A = ![]()
Prueba:
Tomemos LHS
bronceado 3A = bronceado(2A + A)
Usando la identidad
Obtenemos
bronceado 3A =
=
=
=
Ejemplo 1. Resuelve 2sin3xsenx.
Solución:
Tenemos 2sen3xsenx
También escribimos como y = y1. y2 ….(1)
Aquí, y1 = 2sen3x
y2 = senx
Entonces resolvamos y1 = 2sin3x
Usando la identidad
sen 3A = 3 sen A – 4 sen 3 A
Obtenemos
y1 = 2(sen x – 4 sen 3 x)
= 2 sen x – 8 sen 3 x
Ahora pon estos valores en la ecuación (1), obtenemos
y = (2sen x – 8 sen 3 x)(senx)
= 2 sen 2 x – 8 sen 4 x
Ejemplo 2. Resuelve 2tan3xtanx.
Solución:
Tenemos 2tan3xtanx
También escribimos como y = y1. y2 ….(1)
Aquí, y1 = 2tan3x
y2 = tanx
Entonces resolvamos y1 = 2tan3x
Usando la identidad
bronceado 3A =
Obtenemos
y1 = 2(
)
=
Ahora pon estos valores en la ecuación (1), obtenemos
y = (
)(tanx)
=
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA