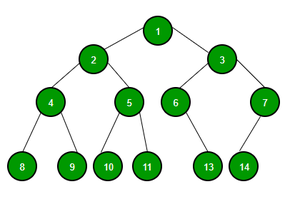
Generación de árbol binario no ponderado aleatorio :
- Dado que se trata de un árbol, el plan de generación de datos de prueba es tal que no se forma ningún ciclo.
- El número de aristas es uno menos que el número de vértices.
- Para cada EJECUCIÓN , primero imprima el recuento de Nodes, por ejemplo, N y las siguientes N – 1 líneas son de la forma (a, b) donde a es el padre de b.
- Cada Node contiene como máximo 2 hijos.
Enfoque: El problema se puede resolver usando Queue . La idea es atravesar el árbol usando BFS . Siga los pasos a continuación para resolver el problema:
- Inicialice un mapa , diga mp para verificar si un Node ya está incluido en el árbol o no.
- Inicialice una cola para almacenar los Nodes en cada nivel del árbol.
- Considere 1 como Node raíz e insértelo en la cola.
- Iterar sobre la cola mientras el recuento total de Nodes en el árbol no sea igual a N . En cada iteración , inserte Nodes distintos de cada nivel del árbol en la cola usando la función rand() y el mapa , también inserte el Node y el padre del Node en una array
- Finalmente, imprima el valor de N y la array.
CPP
// C++ Program to generate test cases for
// an unweighted tree
#include <bits/stdc++.h>
using namespace std;
// Function to generate the binary tree using BFS
vector<pair<int, int> > generateBinaryTree(int n)
{
// Stores number of children
// a node can have
vector<int> options = { 0, 1, 2 };
// Check if a node is already
// included in the tree or not
map<int, int> mp;
// Stores node of tree at
// each level of the tree
queue<int> q;
// Insert root node
q.push(1);
// Stores the generated tree
vector<pair<int, int> > v;
// Store count of nodes
// already included
int count = 1;
// Marking the inclusion
// of node 1
mp[1] = 1;
// Traverse tree using BFS
while (!q.empty() or count < n) {
// Stores from element
// of queue
int front;
if(!q.empty()) {
// Update front
front = q.front();
// Pop front element
// of queue
q.pop();
}
// Find count of child nodes
// of current node
int numberOfChilds
= options[rand() % (options.size())];
// If all the nodes are
// already included
if (count >= n)
continue;
// Connect child node to
// the parent node
while (numberOfChilds--) {
// Stores value in node which
// is not already included
int child = rand() % n + 1;
// Find the child until found a node
// that is not yet included
while (mp[child]) {
child++;
if (child > n) {
child = 1;
}
}
// Update count
count++;
// Mark the included node
mp[child] = 1;
// Insert it to the generated tree
// as {parent, child}
v.push_back({ front, child });
// Push the child into the queue
q.push(child);
// If all the nodes are included
// break
if (count == n)
break;
}
}
// Shuffle the v vector randomly
random_shuffle(v.begin(), v.end());
return v;
}
// Function to print the generated tree
void printTree(int n, vector<pair<int, int> > v)
{
int s = v.size();
// Number of nodes
cout << n << "\n";
// Print n-1 edges as {parent, child}
for (int i = 0; i < v.size(); i++) {
cout << v[i].first << " " << v[i].second << "\n";
}
}
// Driver Code
int main()
{
// Random seeding
srand(time(NULL));
// Number of node between 3 to 8
// this range can be easily changed
int n = rand() % 6 + 3;
// Function Call
vector<pair<int, int> > v
= generateBinaryTree(n);
// Print the generated tree
printTree(n, v);
}
Producción:
5 5 4 1 2 1 3 3 5
Publicación traducida automáticamente
Artículo escrito por dhananjayrohmetra y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA