Generar elementos de la array siguiendo las condiciones dadas

Dado un número entero N, para cada número entero i en el rango de 2 a N , asigne un número entero positivo  tal que se cumplan las siguientes condiciones: 
 

• Para cualquier par de índices (i, j) , si i y j son coprimos entonces  .
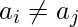• El valor máximo de todos 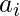 debe minimizarse (es decir, el valor máximo debe ser lo más pequeño posible).

Un par de enteros se llama coprimos si su mcd(i, j) = 1.
Ejemplos: 
 

Entrada: N = 4 
Salida: 1 2 1 
Entrada: N = 10 
Salida: 1 2 1 3 2 4 1 2 3 
 

Enfoque: debemos tener en cuenta dos cosas al asignar valores en los índices de 2 a n . Primero, para cualquier par (i, j) , si i y j son coprimos entonces no podemos asignar el mismo valor a este par de índices. En segundo lugar, tenemos que minimizar el valor máximo asignado a cada índice de 2 a n .
Esto se puede lograr si se asignan números distintos a cada primo porque todos los primos son coprimos entre sí. Luego asigne valores en todas las posiciones compuestas iguales a cualquiera de sus divisores primos. Esta solución funciona como para cualquier par (i, j) , i recibe el mismo número de un divisor y tambiénj , por lo que si son coprimos, no se les puede dar el mismo número.
Este enfoque se puede implementar haciendo un pequeño cambio al construir el Tamiz de Eratóstenes . 
Cuando nos encontremos con un número primo por primera vez, entonces asigne un valor único más pequeño a él y a todos sus múltiplos. De esta forma, todos los índices primos deben tener valores únicos y todos los índices compuestos han valorado lo mismo que cualquiera de sus divisores primos.
A continuación se muestra la implementación del enfoque anterior: 
 

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to generate the required array
void specialSieve(int n)
{
 
    // Initialize cnt variable for assigning
    // unique value to prime and its multiples
    int cnt = 0;
    int prime[n + 1];
 
    for (int i = 0; i <= n; i++)
        prime[i] = 0;
 
    for (int i = 2; i <= n; i++) {
 
        // When we get a prime for the first time
        // then assign a unique smallest value to
        // it and all of its multiples
        if (!prime[i]) {
            cnt++;
            for (int j = i; j <= n; j += i)
                prime[j] = cnt;
        }
    }
 
    // Print the generated array
    for (int i = 2; i <= n; i++)
        cout << prime[i] << " ";
}
 
// Driver code
int main()
{
    int n = 6;
 
    specialSieve(n);
 
    return 0;
}

// Java implementation of the approach
import java.io.*;
 
class GFG
{
 
// Function to generate the required array
static void specialSieve(int n)
{
 
    // Initialize cnt variable for assigning
    // unique value to prime and its multiples
    int cnt = 0;
    int prime[] = new int[n+1];
 
    for (int i = 0; i <= n; i++)
        prime[i] = 0;
 
    for (int i = 2; i <= n; i++)
    {
 
        // When we get a prime for the first time
        // then assign a unique smallest value to
        // it and all of its multiples
        if (!(prime[i]>0))
        {
            cnt++;
            for (int j = i; j <= n; j += i)
                prime[j] = cnt;
        }
    }
 
    // Print the generated array
    for (int i = 2; i <= n; i++)
        System.out.print(prime[i] + " ");
}
 
// Driver code
public static void main (String[] args)
{
    int n = 6;
 
specialSieve(n);
 
}
}
 
// This code is contributed by anuj_67..

# Python3 implementation of the approach
 
# Function to generate the required array
def specialSieve(n) :
 
    # Initialize cnt variable for assigning
    # unique value to prime and its multiples
    cnt = 0;
    prime = [0]*(n + 1);
 
    for i in range(2, n + 1) :
 
        # When we get a prime for the first time
        # then assign a unique smallest value to
        # it and all of its multiples
        if (not prime[i]) :
            cnt += 1;
            for j in range(i, n + 1, i) :
                prime[j] = cnt;
 
    # Print the generated array
    for i in range(2, n + 1) :
        print(prime[i],end = " ");
 
 
# Driver code
if __name__ == "__main__" :
 
    n = 6;
    specialSieve(n);
     
# This code is contributed by AnkitRai01

// C# implementation of the approach
using System;
 
class GFG
{
 
// Function to generate the required array
static void specialSieve(int n)
{
 
    // Initialize cnt variable for assigning
    // unique value to prime and its multiples
    int cnt = 0;
    int []prime = new int[n+1];
 
    for (int i = 0; i <= n; i++)
        prime[i] = 0;
 
    for (int i = 2; i <= n; i++)
    {
 
        // When we get a prime for the first time
        // then assign a unique smallest value to
        // it and all of its multiples
        if (!(prime[i] > 0))
        {
            cnt++;
            for (int j = i; j <= n; j += i)
                prime[j] = cnt;
        }
    }
 
    // Print the generated array
    for (int i = 2; i <= n; i++)
        Console.Write(prime[i] + " ");
}
 
// Driver code
public static void Main ()
{
    int n = 6;
 
    specialSieve(n);
 
}
}
 
// This code is contributed by anuj_67..

<script>
 
// Javascript implementation of the approach
 
// Function to generate the required array
function specialSieve(n)
{
 
    // Initialize cnt variable for assigning
    // unique value to prime and its multiples
    let cnt = 0;
    let prime = new Array(n + 1);
 
    for (let i = 0; i <= n; i++)
        prime[i] = 0;
 
    for (let i = 2; i <= n; i++) {
 
        // When we get a prime for the first time
        // then assign a unique smallest value to
        // it and all of its multiples
        if (!prime[i]) {
            cnt++;
            for (let j = i; j <= n; j += i)
                prime[j] = cnt;
        }
    }
 
    // Print the generated array
    for (let i = 2; i <= n; i++)
        document.write(prime[i] + " ");
}
 
// Driver code
    let n = 6;
 
    specialSieve(n);
 
</script>

1 2 1 3 2

Complejidad de tiempo: O (N Log N)

Espacio Auxiliar: O(N)