El gráfico espectral se utiliza para demostrar la única frecuencia dominante del gráfico. Esto indica que el modelo sinusoidal de ciclo único podría ser apropiado.
Considere la gráfica anterior, supongamos que la gráfica tiene la siguiente distribución:
![]()
Ahora, tratamos de estimar la constante por la media muestral. Este tipo de análisis conduciría a una conclusión incorrecta porque:
- La media de la muestra está sesgada.
- El intervalo de confianza (IC) para la media es demasiado pequeño.
Aquí, la elección adecuada del modelo es como![]()
![]()
donde, a (alfa) es la amplitud, w (omega) es la frecuencia de la observación y phi es la diferencia de fase.
Los siguientes pasos después de esto:
- Estime la frecuencia de la gráfica espectral, esto sería útil para iniciar el valor del ajuste no lineal subsiguiente. Podemos usar el diagrama de fase de demodulación compleja para estimarlo.
- Realice una gráfica de amplitud de demodulación compleja para estimar la amplitud de la gráfica y determinar si una amplitud constante es suficiente.
- Realice un ajuste no lineal del modelo en el conjunto de datos.
![]()
Implementación:
- En esta implementación, usaremos un estudio de caso de deflexión de haz, el conjunto de datos se puede descargar desde aquí .
Python3
# necessary imports
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
%matplotlib inline
sns.mpl.rcParams['figure.figsize'] = (20.0, 15.0)
# read beam data
beam_data = pd.read_csv('beam_Deflection.txt', header=None)
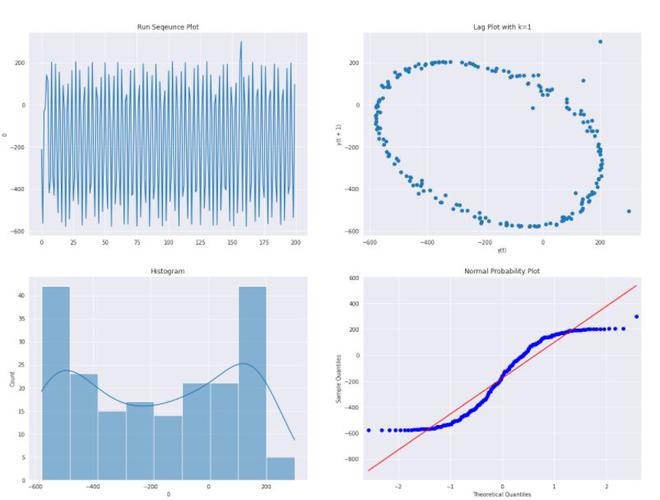
# draw 4 plot
sns.set_style('darkgrid')
fig, ax = plt.subplots(2,2)
sns.lineplot(x= pd.Series(beam_data.index),y =beam_data[0],ax =ax[0,0])
ax[0,0].set_title('Run Sequence Plot')
pd.plotting.lag_plot(beam_data[0],ax =ax[0,1])
ax[0,1].set_title('Lag Plot with k=1')
sns.histplot(beam_data[0],kde=True,ax =ax[1,0])
ax[1,0].set_title('Histogram')
sm.ProbPlot(beam_data[0]).qqplot(line='s', ax=ax[1,1],color='blue');
ax[1,1].set_title('Normal Probability Plot')
fig.suptitle('4-plot')
plt.show()
- El gráfico de 4 (gráfico de retardo) muestra claramente que hay algún tipo de función periódica que se puede usar para describir el conjunto de datos. Ahora, supongamos que los datos se pueden ajustar mediante la siguiente ecuación:
![]()
- Ahora, trazamos el gráfico de fase de demodulación compleja y el gráfico de amplitud de demodulación compleja para obtener la frecuencia y la amplitud de la ecuación anterior. Puede obtener más información sobre cómo trazar una fase de demodulación compleja y un gráfico de amplitud desde aquí .
- El gráfico de fase de demodulación compleja da una frecuencia de 0,3025 y el gráfico de amplitud de demodulación compleja da una amplitud de alrededor de 390 después de un arranque en frío.