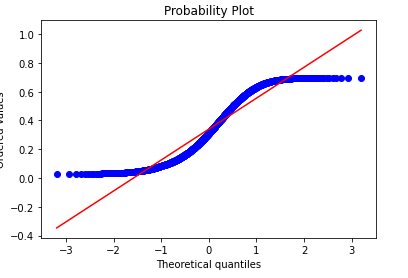
La gráfica cuantil-cuantil es un método gráfico para determinar si dos muestras de datos provienen de la misma población o no. Una gráfica qq es una gráfica de los cuantiles del primer conjunto de datos contra los cuantiles del segundo conjunto de datos. Por cuantil, nos referimos a la fracción (o porcentaje) de puntos por debajo del valor dado.
Para fines de referencia, también se traza una línea del 45%, si las muestras son de la misma población, los puntos están a lo largo de esta línea.
Distribución normal:
La distribución normal (también conocida como distribución gaussiana/curva de campana) es una distribución de probabilidad continua que representa la distribución obtenida de los valores reales generados aleatoriamente.
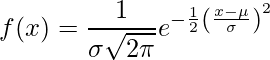

A continuación se muestra la porción de datos que representan diferentes desviaciones estándar

Distribución normal con área bajo la curva
Uso:
El gráfico Cuantil-Cuantil se utiliza para el siguiente propósito:
- Determinar si dos muestras son de la misma población.
- Si dos muestras tienen la misma cola
- Si dos muestras tienen la misma forma de distribución.
- Si dos muestras tienen un comportamiento de ubicación común.
Cómo dibujar un gráfico QQ
- Recopile los datos para trazar el gráfico cuantil-cuantil.
- Ordena los datos en orden ascendente o descendente.
- Dibujar una curva de distribución normal.
- Encuentre el valor z (punto de corte) para cada segmento.
- Trace los valores del conjunto de datos contra los puntos de corte de normalización.
Ventajas de la trama QQ
- Dado que la gráfica QQ es como una gráfica de probabilidad. Entonces, al comparar dos conjuntos de datos, el tamaño de la muestra no necesita ser igual.
- Dado que necesitamos normalizar el conjunto de datos, no es necesario que nos preocupemos por las dimensiones de los valores.
Tipos de gráficos QQ
- Para distribución de cola izquierda: A continuación se muestra el
- Para la distribución uniforme: A continuación se muestra la distribución de la parcela qq para la distribución uniforme:

gráfico QQ de distribución uniforme
Implementación de código Python
# code
import scipy.stats as stats
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
n = 2000
observation = np.random.binomial(n, 0.53, size=1000)/n
z = (observation-np.mean(observation))/np.std(observation)
stats.probplot(z, dist="norm", plot=plt)
plt.title("Normal Q-Q plot")
plt.show()
Producción:

Gráfica QQ normal