Gráficos lineales

En el caso de dos variables cualesquiera, la relación entre estas dos variables se puede dibujar construyendo la tabla de valores si se menciona la regla para esa relación. Se deben conocer las coordenadas de al menos dos puntos para trazar un gráfico de línea recta. Estos puntos deben ajustarse a la regla y dichos gráficos, cuando se dibujan, se denominan gráficos lineales.

gráficos lineales

Un gráfico lineal que tiene una línea continua se llama gráfico lineal. Para dibujar la línea continua, necesitamos ubicar algunos puntos en la hoja de gráficos.

Hagamos un gráfico que tenga la coordenada x y la coordenada y.

Suponga que va a un auditorio y busca su asiento reservado. Necesita saber dos números, el número de fila y el número de asiento. Este es el método básico para fijar un punto en un plano.

¿Cómo se puede describir la ubicación en el tablero?

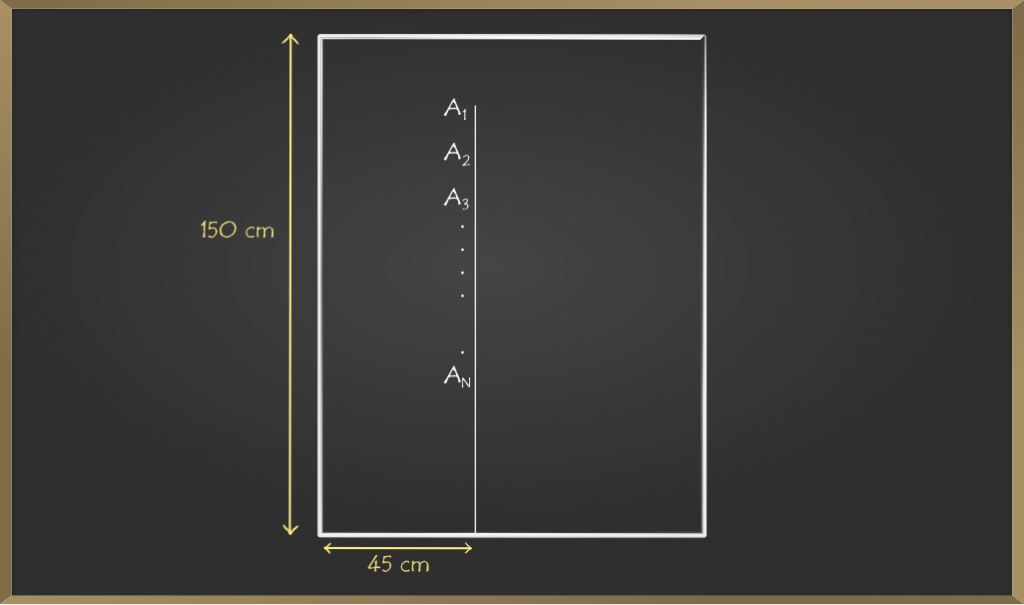
Dibujar un punto en el tablero, a saber, A1, A2, A3, …., AN midiendo estos puntos desde el borde izquierdo del tablero y se encuentra que mide 45 cm. Ahora podemos decir que A1 está a 45 cm del borde izquierdo ya 150 cm del borde inferior.

Ejemplos de problemas en gráficas lineales

Problema 1: Marca (3, 4) en el gráfico 

Solución: 

Como en el gráfico, los puntos se denotan en forma de (x, y)

Entonces, al comparar los puntos:

x = 3 y y = 4. 

Primero, dibuje x = 3 movimientos en la dirección de avance a x = 3. 

Ahora, dibuje y = 4 se mueve hacia arriba a (3, 4).

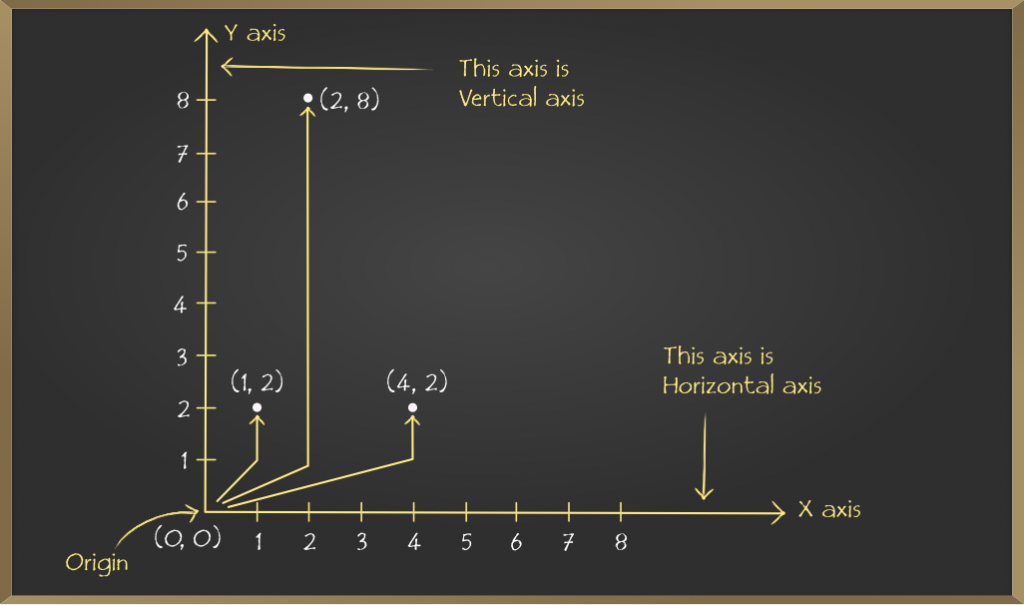
Problema 2: Ubica los puntos dados en el gráfico.

1. (1, 2)
2. (2, 8)
3. (4, 2)

Solución:

Para x = 1 y y = 2. Comenzando desde el origen (0, 0), movemos x = 1 dirección hacia adelante y desde allí movemos y = 2 dirección hacia arriba y finalmente alcanzar el estado es nuestro punto.

De manera similar, trace el resto de los dos puntos en Graph.

Problema 3: Grafica los siguientes puntos y verifica si están en la línea.

1. (0, 1), (0, 2), (0, 4), (0, 3)
2. (1, 1), (2, 2), (3, 3), (4, 4), (5, 5)

Solución: 

1. Trazar (0, 1), (0, 2), (0, 4), (0, 3) en el gráfico

Podemos dibujar cada coordenada en la hoja de gráficos de la siguiente manera.

Aquí forma una línea después de unir todos los puntos.

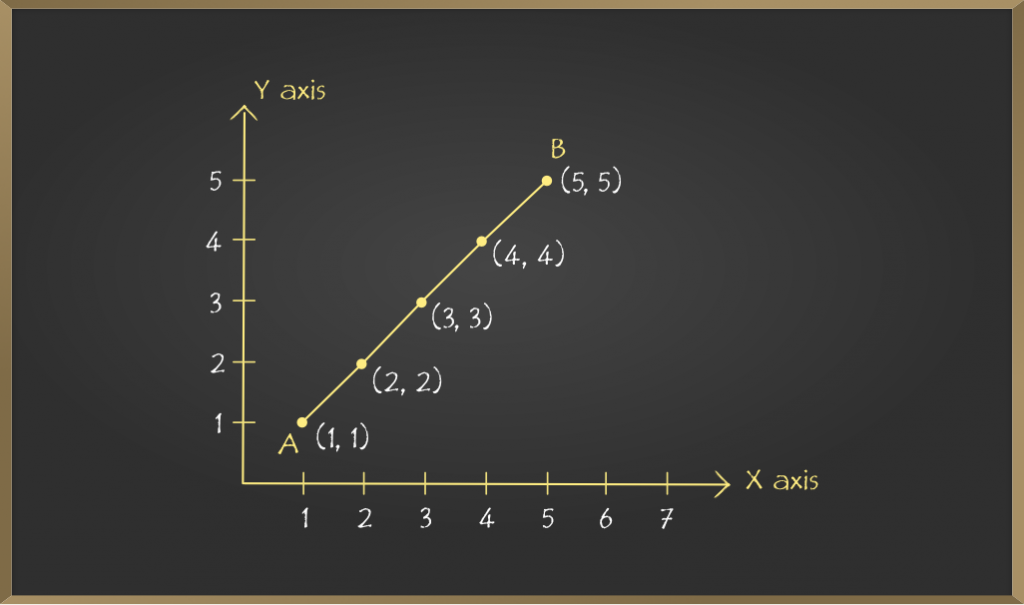
 2. Trazar (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) en un gráfico

        

Nota: En cada uno de los casos anteriores, el gráfico obtenido al unir los puntos trazados es una línea. Estos gráficos se denominan gráficos lineales.

Aplicación de Gráficos Lineales

En la vida cotidiana observamos variaciones en el valor de diferentes cantidades, o podemos decir que cuanto más usamos la instalación más tenemos que pagar por ella. por ejemplo si cuanta más electricidad consumimos entonces tendremos que pagar más la factura y viceversa. Así que una cantidad afecta a la otra cantidad. Podemos decir que la cantidad de electricidad es la variable independiente y el monto de la factura es la variable dependiente. Estas relaciones las podemos mostrar con gráficas. 

Problema 1: Amit puede andar en bicicleta con una velocidad constante de 30 km/hora. Dibuja una gráfica de tiempo-distancia para esta situación y encuéntrala 

(i) Tiempo que tarda Amit en recorrer 75 km.

(ii) Distancia recorrida por Amit en 3,5 horas.

Solución: 

Horas de paseo	Distancia recorrida
1 hora 2 horas 3 horas 4 horas	30 kilómetros 2*30 = 60km 3*30 = 90km 4*30 = 120 km

La tabla así formada es:

Tiempo (en horas)	1	2	3	4
Distancia recorrida (en km)	30	60	90	120

Considere la escala: 

Horizontal: 2 unidades = 1 hora

Vertical: 1 unidad = 10 km

Marque el tiempo en el eje horizontal.

Marcar la distancia en el eje vertical

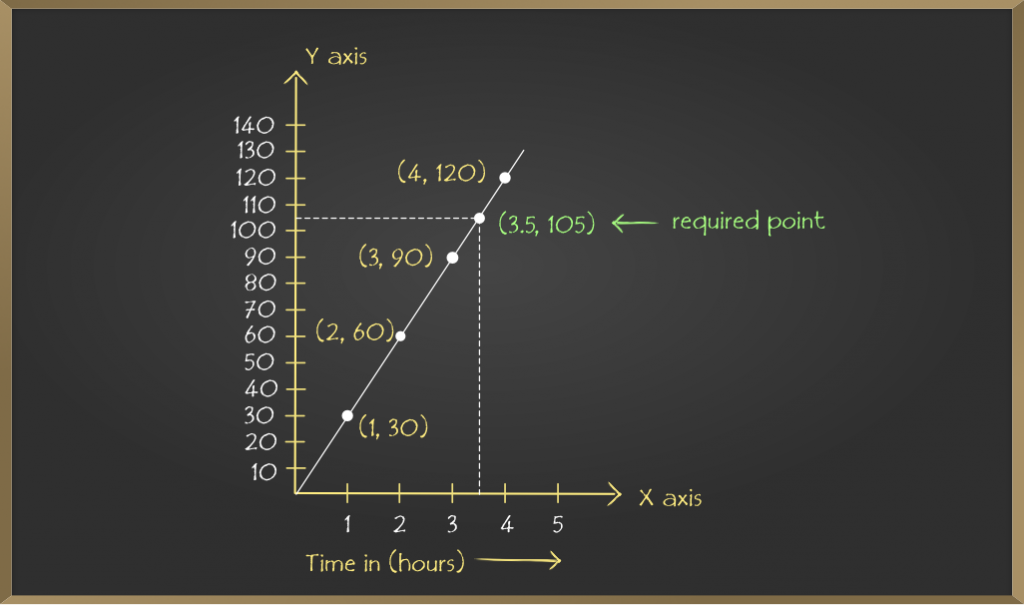
Puntos de trama: (1, 30), (2, 60), (3, 90), (4, 120)

Al unir los puntos se obtiene la gráfica lineal requerida.

(i) Del gráfico anterior se concluye que en el eje vertical correspondiente a la distancia de 75 km, el tiempo es de 2,5 horas en el eje horizontal. Por lo tanto, se necesitan 2,5 horas para recorrer 75 km. 

(ii) De manera similar, en el eje horizontal correspondiente al tiempo de 3,5 horas, la distancia recorrida es de 105 km en el eje vertical.

Problema 2: Un banco público ofrece un interés del 10% sobre los depósitos de los adultos mayores. Trace un gráfico que represente la relación entre la cantidad depositada y el interés que ganan los adultos mayores y establezca lo siguiente del gráfico así trazado:

(i) El interés devengado anualmente por una inversión de 450.

(ii) La cantidad de dinero depositada para ganar el interés de 5.

Monto depositado (en )	100	300	500	700	900
Interés ganado (en )	10	30	50	70	90

Solución:

Considere la escala: 

Horizontales: 1 unidad =

Verticales: 1 unidad =

Marque el interés ganado en el eje horizontal.

Marque la cantidad depositada en el eje vertical.

Marca los puntos: (10, 100), (30, 300), (50, 500), (70, 700) y (90, 900) en el gráfico.

Al unir los puntos se obtiene la gráfica lineal requerida.

(i) Del gráfico anterior se concluye que en el eje vertical correspondiente a la cantidad depositada, en el eje horizontal se encuentra el interés devengado. Así, se ganan en el depósito de 

(ii) Asimismo, en el eje horizontal correspondiente a los intereses devengados del 35%, en el eje vertical se encuentra el importe depositado .