Grupos mínimos bipartitos

Posted on by Rudeus Greyrat

Dada la representación de la lista de adyacencia del gráfico de N vértices de 1 a N , la tarea es contar los grupos bipartitos mínimos del gráfico dado.

Ejemplos: 

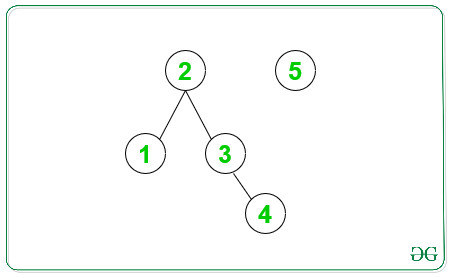
Entrada: N = 5 
A continuación se muestra el gráfico dado con un número de Nodes de 5: 
 

Salida: 3 
Explicación: 
Posibles grupos que satisfacen la propiedad Bipartita: [2, 5], [1, 3], [4] 
A continuación se muestra el número de grupos bipartitos que se pueden formar: 
 

Enfoque: 
La idea es encontrar la altura máxima de todos los componentes conectados en el gráfico dado de N Nodes para encontrar los grupos bipartitos mínimos. A continuación se muestran los pasos: 

  1. Para todos los vértices no visitados en el gráfico dado, encuentre la altura de los componentes conectados actuales a partir del vértice actual.
  2. Inicie DFS Traversal para encontrar la altura de todos los componentes conectados.
  3. El máximo de las alturas calculadas para todos los Componentes Conectados da los grupos bipartitos mínimos requeridos.

A continuación se muestra la implementación del enfoque anterior: 

C++

#include <bits/stdc++.h>
using namespace std;
 
// Function to find the height sizeof
// the current component with vertex s
int height(int s, vector<int> adj[],
           int* visited)
{
    // Visit the current Node
    visited[s] = 1;
    int h = 0;
 
    // Call DFS recursively to find the
    // maximum height of current CC
    for (auto& child : adj[s]) {
 
        // If the node is not visited
        // then the height recursively
        // for next element
        if (visited[child] == 0) {
            h = max(h, 1 + height(child, adj,
                                  visited));
        }
    }
    return h;
}
 
// Function to find the minimum Groups
int minimumGroups(vector<int> adj[], int N)
{
    // Initialise with visited array
    int visited[N + 1] = { 0 };
 
    // To find the minimum groups
    int groups = INT_MIN;
 
    // Traverse all the non visited Node
    // and calculate the height of the
    // tree with current node as a head
    for (int i = 1; i <= N; i++) {
 
        // If the current is not visited
        // therefore, we get another CC
        if (visited[i] == 0) {
            int comHeight;
            comHeight = height(i, adj, visited);
            groups = max(groups, comHeight);
        }
    }
 
    // Return the minimum bipartite matching
    return groups;
}
 
// Function that adds the current edges
// in the given graph
void addEdge(vector<int> adj[], int u, int v)
{
    adj[u].push_back(v);
    adj[v].push_back(u);
}
 
// Drivers Code
int main()
{
    int N = 5;
 
    // Adjacency List
    vector<int> adj[N + 1];
 
    // Adding edges to List
    addEdge(adj, 1, 2);
    addEdge(adj, 3, 2);
    addEdge(adj, 4, 3);
 
    cout << minimumGroups(adj, N);
}

Java

import java.util.*;
 
class GFG{
  
// Function to find the height sizeof
// the current component with vertex s
static int height(int s, Vector<Integer> adj[],
           int []visited)
{
    // Visit the current Node
    visited[s] = 1;
    int h = 0;
  
    // Call DFS recursively to find the
    // maximum height of current CC
    for (int  child : adj[s]) {
  
        // If the node is not visited
        // then the height recursively
        // for next element
        if (visited[child] == 0) {
            h = Math.max(h, 1 + height(child, adj,
                                  visited));
        }
    }
    return h;
}
  
// Function to find the minimum Groups
static int minimumGroups(Vector<Integer> adj[], int N)
{
    // Initialise with visited array
    int []visited= new int[N + 1];
  
    // To find the minimum groups
    int groups = Integer.MIN_VALUE;
  
    // Traverse all the non visited Node
    // and calculate the height of the
    // tree with current node as a head
    for (int i = 1; i <= N; i++) {
  
        // If the current is not visited
        // therefore, we get another CC
        if (visited[i] == 0) {
            int comHeight;
            comHeight = height(i, adj, visited);
            groups = Math.max(groups, comHeight);
        }
    }
  
    // Return the minimum bipartite matching
    return groups;
}
  
// Function that adds the current edges
// in the given graph
static void addEdge(Vector<Integer> adj[], int u, int v)
{
    adj[u].add(v);
    adj[v].add(u);
}
  
// Drivers Code
public static void main(String[] args)
{
    int N = 5;
  
    // Adjacency List
    Vector<Integer> []adj = new Vector[N + 1];
    for (int i = 0 ; i < N + 1; i++)
        adj[i] = new Vector<Integer>();
     
    // Adding edges to List
    addEdge(adj, 1, 2);
    addEdge(adj, 3, 2);
    addEdge(adj, 4, 3);
  
    System.out.print(minimumGroups(adj, N));
}
}
 
// This code is contributed by 29AjayKumar

Python3

import sys
 
# Function to find the height sizeof
# the current component with vertex s
def height(s, adj, visited):
 
    # Visit the current Node
    visited[s] = 1
    h = 0
  
    # Call DFS recursively to find the
    # maximum height of current CC
    for child in adj[s]:
  
        # If the node is not visited
        # then the height recursively
        # for next element
        if (visited[child] == 0):
            h = max(h, 1 + height(child, adj,
                                  visited))
     
    return h
 
# Function to find the minimum Groups
def minimumGroups(adj, N):
 
    # Initialise with visited array
    visited = [0 for i in range(N + 1)]
  
    # To find the minimum groups
    groups = -sys.maxsize
  
    # Traverse all the non visited Node
    # and calculate the height of the
    # tree with current node as a head
    for i in range(1, N + 1):
  
        # If the current is not visited
        # therefore, we get another CC
        if (visited[i] == 0):
            comHeight = height(i, adj, visited)
            groups = max(groups, comHeight)
         
    # Return the minimum bipartite matching
    return groups
 
# Function that adds the current edges
# in the given graph
def addEdge(adj, u, v):
     
    adj[u].append(v)
    adj[v].append(u)
 
# Driver code   
if __name__=="__main__":
     
    N = 5
  
    # Adjacency List
    adj = [[] for i in range(N + 1)]
  
    # Adding edges to List
    addEdge(adj, 1, 2)
    addEdge(adj, 3, 2)
    addEdge(adj, 4, 3)
  
    print(minimumGroups(adj, N))
 
# This code is contributed by rutvik_56

C#

using System;
using System.Collections.Generic;
 
class GFG{
   
// Function to find the height sizeof
// the current component with vertex s
static int height(int s, List<int> []adj,
           int []visited)
{
    // Visit the current Node
    visited[s] = 1;
    int h = 0;
   
    // Call DFS recursively to find the
    // maximum height of current CC
    foreach (int  child in adj[s]) {
   
        // If the node is not visited
        // then the height recursively
        // for next element
        if (visited[child] == 0) {
            h = Math.Max(h, 1 + height(child, adj,
                                  visited));
        }
    }
    return h;
}
   
// Function to find the minimum Groups
static int minimumGroups(List<int> []adj, int N)
{
    // Initialise with visited array
    int []visited= new int[N + 1];
   
    // To find the minimum groups
    int groups = int.MinValue;
   
    // Traverse all the non visited Node
    // and calculate the height of the
    // tree with current node as a head
    for (int i = 1; i <= N; i++) {
   
        // If the current is not visited
        // therefore, we get another CC
        if (visited[i] == 0) {
            int comHeight;
            comHeight = height(i, adj, visited);
            groups = Math.Max(groups, comHeight);
        }
    }
   
    // Return the minimum bipartite matching
    return groups;
}
   
// Function that adds the current edges
// in the given graph
static void addEdge(List<int> []adj, int u, int v)
{
    adj[u].Add(v);
    adj[v].Add(u);
}
   
// Drivers Code
public static void Main(String[] args)
{
    int N = 5;
   
    // Adjacency List
    List<int> []adj = new List<int>[N + 1];
    for (int i = 0 ; i < N + 1; i++)
        adj[i] = new List<int>();
      
    // Adding edges to List
    addEdge(adj, 1, 2);
    addEdge(adj, 3, 2);
    addEdge(adj, 4, 3);
   
    Console.Write(minimumGroups(adj, N));
}
}
  
// This code is contributed by Rajput-Ji

Javascript

<script>
 
 
// Function to find the height sizeof
// the current component with vertex s
function height(s, adj, visited)
{
    // Visit the current Node
    visited[s] = 1;
    var h = 0;
 
    // Call DFS recursively to find the
    // maximum height of current CC
    adj[s].forEach(child => {
         
 
        // If the node is not visited
        // then the height recursively
        // for next element
        if (visited[child] == 0) {
            h = Math.max(h, 1 + height(child, adj,
                                  visited));
        }
    });
    return h;
}
 
// Function to find the minimum Groups
function minimumGroups(adj, N)
{
    // Initialise with visited array
    var visited = Array(N+1).fill(0);
 
    // To find the minimum groups
    var groups = -1000000000;
 
    // Traverse all the non visited Node
    // and calculate the height of the
    // tree with current node as a head
    for (var i = 1; i <= N; i++) {
 
        // If the current is not visited
        // therefore, we get another CC
        if (visited[i] == 0) {
            var comHeight;
            comHeight = height(i, adj, visited);
            groups = Math.max(groups, comHeight);
        }
    }
 
    // Return the minimum bipartite matching
    return groups;
}
 
// Function that adds the current edges
// in the given graph
function addEdge(adj, u, v)
{
    adj[u].push(v);
    adj[v].push(u);
}
 
// Drivers Code
var N = 5;
 
// Adjacency List
var adj = Array.from(Array(N+1), ()=>Array())
 
// Adding edges to List
addEdge(adj, 1, 2);
addEdge(adj, 3, 2);
addEdge(adj, 4, 3);
 
document.write( minimumGroups(adj, N));
 
 
 
</script>
Producción: 

3

 

Complejidad Temporal: O(V+E), donde V es el número de vértices y E es el conjunto de aristas.
Espacio Auxiliar : O(V). 

Publicación traducida automáticamente

Artículo escrito por king_tsar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *