Encuentre el valor de cos(405)°

La trigonometría es una disciplina de las matemáticas que estudia las relaciones entre las longitudes de los lados y los ángulos de un triángulo rectángulo. Las funciones trigonométricas, también conocidas como funciones goniométricas, funciones angulares o funciones circulares, son funciones que establecen la relación entre un ángulo y la razón de dos de los lados de un triángulo rectángulo. Las seis funciones trigonométricas principales son seno, coseno, tangente, cotangente, secante o cosecante.

Los ángulos definidos por las proporciones de las funciones trigonométricas se conocen como ángulos trigonométricos. Los ángulos trigonométricos representan funciones trigonométricas. El valor del ángulo puede estar entre 0 y 360°.

Identidades trigonométricas

Las igualdades que involucran funciones trigonométricas que son verdaderas para cada valor de las variables que ocurren para las cuales ambos lados de la igualdad están definidos se conocen como identidades trigonométricas. Los diversos tipos de identidades trigonométricas son los siguientes,

Identidades recíprocas

$\newline \sin \theta= \frac{1}{\cosec \theta} \newline \cos \theta= \frac{1}{\sec \theta} \newline \tan \theta= \frac{1}{\cot \theta} \newline \cot \theta= \frac{1}{\tan \theta} \newline \sec \theta= \frac{1}{\cos \theta} \newline \cosec \theta= \frac{1}{\sin \theta}$

Identidades trigonométricas pitagóricas

$\sin^2θ + \cos^2θ = 1 \newline \sec^2θ-\tan^2θ = 1 \newline \cosec^2θ-\cot^2θ = 1$

Identidades trigonométricas complementarias y suplementarias

Los ángulos complementarios son un par de ángulos cuya suma es igual a 90°. (90° $-\theta$ ) es el complemento de un ángulo $\theta$ . Las siguientes son las razones trigonométricas de los ángulos complementarios,

$\sin(\frac{\pi}{2}-\theta)=\cos\theta \newline \cos(\frac{\pi}{2}-\theta)=\sin\theta \newline \tan(\frac{\pi}{2}-\theta)=\cot\theta \newline \cot(\frac{\pi}{2}-\theta)=\tan\theta \newline \sec(\frac{\pi}{2}-\theta)=\cosec\theta \newline \cosec(\frac{\pi}{2}-\theta)=\sec\theta$

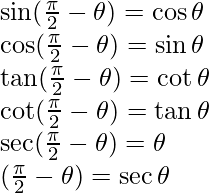
Los ángulos suplementarios son un par de ángulos cuya suma es igual a 180°. 180° $-\theta$ es el suplemento de un ángulo $\theta$ . Las siguientes son las razones trigonométricas de los ángulos suplementarios,

$\newline \sin(\pi-\theta)=\sin\theta \newline \cos(\pi-\theta)=-\cos\theta \newline \tan(\pi-\theta)=-\tan\theta \newline \cot(\pi-\theta)=-\cot\theta \newline \sec(\pi-\theta)=-\sec\theta \newline \cosec(\pi-\theta)=\cosec\theta$