En matemáticas, las funciones trigonométricas inversas también se conocen como funciones arcus o funciones anti-trigonométricas. Las funciones trigonométricas inversas son las funciones inversas de las funciones trigonométricas básicas, es decir, seno, coseno, tangente, cosecante, secante y cotangente. Se utiliza para encontrar los ángulos con cualquier razón trigonométrica. Las funciones trigonométricas inversas se utilizan generalmente en campos como la geometría, la ingeniería, etc. La representación de las funciones trigonométricas inversas son:
Si a = f(b), entonces la función inversa es
b = f – 1 (a)
Ejemplos de funciones trigonométricas inversas inversas son sin -1 x, cos -1 x, tan -1 x, etc.
La siguiente tabla muestra algunas funciones trigonométricas con su dominio y rango.
| Función | Dominio | Rango |
| y = sen -1 x | [-1, 1] | [-/2, /2] |
| y = cos -1 x | [-1, 1] | [0 , ] |
| y = cosec -1 x | R – (-1,1) | [-/2, /2] – {0} |
| y = seg -1 x | R – (-1, 1) | [0 , ] – {/2} |
| y = bronceado -1 x | R | (-/2, /2) |
| y = cuna -1 x | R | (0 , ) |
Propiedades de las funciones trigonométricas inversas
Las siguientes son las propiedades de las funciones trigonométricas inversas:
Propiedad 1:
- sen -1 (1/x) = cosec -1 x, para x ≥ 1 o x ≤ -1
- cos -1 (1/x) = seg -1 x, para x ≥ 1 o x ≤ -1
- tan -1 (1/x) = cot -1 x, para x > 0
Propiedad 2:
- sen -1 (-x) = -sen -1 x, para x ∈ [-1 , 1]
- tan -1 (-x) = -tan -1 x, para x ∈ R
- cosec -1 (-x) = -cosec -1 x, para |x| ≥ 1
Propiedad 3
- cos -1 (-x) = – cos -1 x, para x ∈ [-1 , 1]
- seg -1 (-x) = – seg -1 x, para |x| ≥ 1
- cot -1 (-x) = – cot -1 x, para x ∈ R
Propiedad 4
- sen -1 x + cos -1 x = /2, para x ∈ [-1,1]
- tan -1 x + cot -1 x = /2, para x ∈ R
- cosec -1 x + sec -1 x = /2 , para |x| ≥ 1
Propiedad 5
- tan -1 x + tan -1 y = tan -1 ( x + y )/(1 – xy), para xy < 1
- tan -1 x – tan -1 y = tan -1 (x – y)/(1 + xy), para xy > -1
- tan -1 x + tan -1 y = + tan -1 (x + y)/(1 – xy), para xy >1 ; x, y >0
Propiedad 6
- 2tan -1 x = sen -1 (2x)/(1 + x 2 ), para |x| ≤ 1
- 2tan -1 x = cos -1 (1 – x 2 )/(1 + x 2 ), para x ≥ 0
- 2tan -1 x = tan -1 (2x)/(1 – x 2 ), para -1 < x <1
Identidades de la función trigonométrica inversa
Las siguientes son las identidades de las funciones trigonométricas inversas:
- sen -1 (sen x) = x siempre que –/2 ≤ x ≤ /2
- cos -1 (cos x) = x siempre que 0 ≤ x ≤
- tan -1 (tan x) = x proporcionado –/2 < x < /2
- sen(sen -1 x) = x siempre que -1 ≤ x ≤ 1
- cos(cos -1 x) = x siempre que -1 ≤ x ≤ 1
- tan(tan -1 x) = x siempre que x ∈ R
- cosec(cosec -1 x) = x siempre que -1 ≤ x ≤ ∞ o -∞ < x ≤ 1
- sec(sec -1 x) = x siempre que 1 ≤ x ≤ ∞ o -∞ < x ≤ 1
- cuna(cuna -1 x) = x siempre -∞ < x < ∞
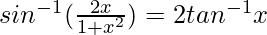
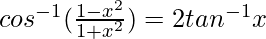
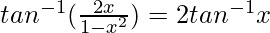
- 2 cos -1 x = cos -1 (2x 2 – 1)
- 2sen -1 x = sen -1 2x√(1 – x 2 )
- 3 sen -1 x = sen -1 (3x – 4x 3 )
- 3 cos -1 x = cos -1 (4x 3 – 3x)
- 3tan -1 x = tan -1 ((3x – x 3 /1 – 3x 2 ))
- sen -1 x + sen -1 y = sen -1 { x√(1 – y 2 ) + y√(1 – x 2 )}
- sen -1 x – sen -1 y = sen -1 { x√(1 – y 2 ) – y√(1 – x 2 )}
- cos -1 x + cos -1 y = cos -1 [xy – √{(1 – x 2 )(1 – y 2 )}]
- cos -1 x – cos -1 y = cos -1 [xy + √{(1 – x 2 )(1 – y 2 )}
- tan -1 x + tan -1 y = tan -1 (x + y/1 – xy)
- bronceado -1 x – bronceado -1 y = bronceado -1 (x – y/1 + xy)
- bronceado -1 x + bronceado -1 y + bronceado -1 z = bronceado -1 (x + y + z – xyz)/(1 – xy – yz – zx)
Problemas de muestra
Pregunta 1: Demostrar sin -1 x = sec -1 1/√(1-x 2 )
Solución:
Sea sen -1 x = y
⇒ sen y = x , (ya que sen y = perpendicular/hipotenusa ⇒ cos y = √(1- perpendicular 2 )/hipotenusa )
⇒ cos y = √(1 – x 2 ), aquí hipotenusa = 1
⇒ seg y = 1/cos y
⇒ segundo y = 1/√(1 – x 2 )
⇒ y = segundo -1 1/√(1 – x 2 )
⇒ sen -1 x = seg -1 1/√(1 – x 2 )
Por lo tanto, probado.
Pregunta 2: Demostrar tan -1 x = cosec -1 √(1 + x 2 )/x
Solución:
Sea tan -1 x = y
⇒ tan y = x , perpendicular = x y base = 1
⇒ sen y = x/√(x 2 + 1) , (ya que hipotenusa = √(perpendicular 2 + base 2 ) )
⇒ cosec y = 1/sen y
⇒ cosec y = √(x 2 + 1)/x
⇒ y = cosec -1 √(x 2 + 1)/x
⇒ tan -1 x = cosec -1 √(x 2 + 1)/x
Por lo tanto, probado.
Pregunta 3: Evaluar tan(cos -1 x)
Solución:
Sea cos -1 x = y
⇒ cos y = x , base = x e hipotenusa = 1 por lo tanto sen y = √(1 – x 2 )/1
⇒ tan y = sen y/ cos y
⇒ tan y = √(1 – x 2 )/x
⇒ y = bronceado -1 √(1 – x 2 )/x
⇒ cos -1 x = tan -1 √(1 – x 2 )/x
Por lo tanto, tan(cos -1 x) = tan(tan -1 √(1 – x 2 )/x ) = √(1 – x 2 )/x.
Pregunta 4: tan -1 √(sen x) + cot -1 √(sen x) = y. Encuentre cos y.
Solución:
Sabemos que tan -1 x + cot -1 x = /2 por lo tanto comparando esta identidad con la ecuación dada en la pregunta obtenemos y = /2
Por tanto, cos y = cos /2 = 0.
Pregunta 5: tan -1 (1 – x)/(1 + x) = (1/2)tan -1 x, x > 0. Resuelva para x.
Solución:
bronceado -1 (1 – x)/(1 + x) = (1/2) bronceado -1 x
⇒ 2tan -1 (1 – x)/(1 + x) = tan -1 x …(1)
Sabemos que, 2tan -1 x = tan -1 2x/(1 – x 2 ).
Por lo tanto, LHS de la ecuación (1) se puede escribir como
bronceado -1 [ { 2(1 – x)/(1 + x)}/{ 1 – [(1 – x)(1 + x)] 2 }]
= bronceado -1 [ {2(1 – x)(1 + x)} / { (1 + x) 2 – (1 – x) 2 }]
= bronceado -1 [ 2(1 – x 2 )/(4x)]
= bronceado -1 (1 – x 2 )/(2x)
Dado que, LHS = RHS por lo tanto
bronceado -1 (1 – x 2 )/(2x) = bronceado -1 x
⇒ (1 – x2 )/ 2x = x
⇒ 1 – x2 = 2×2
⇒ 3×2 = 1
⇒ x = ± 1/√3
Dado que x debe ser mayor que 0, x = 1/√3 es la respuesta aceptable.
Pregunta 6: Demostrar tan -1 √x = (1/2)cos -1 (1 – x)/(1 + x)
Solución:
Sea tan -1 √x = y
⇒ tan y = √x
⇒ tan 2 y = x
Por lo tanto,
RHS = (1/2)cos -1 ( 1- tan 2 y)/(1 + tan 2 y)
= (1/2)cos -1 (cos 2 y – sen 2 y)/(cos 2 y + sen 2 y)
= (1/2) cos -1 (cos 2 y – sen 2 y)
= (1/2)cos -1 (cos 2y)
= (1/2)(2 años)
= y
= bronceado -1 √x
= LHS
Por lo tanto, probado.
Pregunta 7: tan -1 (2x)/(1 – x 2 ) + cot -1 (1 – x 2 )/(2x) = /2, -1 < x < 1. Resuelva para x.
Soluciones:
tan -1 (2x)/(1 – x 2 ) + cot -1 (1 – x 2 )/(2x) = /2
⇒ tan -1 (2x)/(1 – x 2 ) + tan -1 (2x)/(1 – x 2 ) = /2
⇒ 2 tan -1 (2x)/(1 – x 2 ) = ∏/2
⇒ bronceado -1 (2x)/(1 – x 2 ) = ∏/4
⇒ (2x)/(1 – x 2 ) = tan ∏/4
⇒ (2x)/(1 – x2 ) = 1
⇒ 2x = 1 – x2
⇒ x2 + 2x -1 = 0
⇒ x = [-2 ± √(2 2 – 4(1)(-1))] / 2
⇒ x = [-2 ± √8] / 2
⇒ x = -1 ± √2
⇒ x = -1 + √2 o x = -1 – √2
Pero de acuerdo a la pregunta x ∈ (-1, 1) por lo tanto para la ecuación dada el conjunto solución es x ∈ ∅.
Pregunta 8: tan -1 1/(1 + 1,2) + tan -1 1/(1 + 2,3) + … + tan -1 1/(1 + n(n + 1)) = tan -1 x. Solución para x.
Solución:
bronceado -1 1/(1 + 1,2) + bronceado -1 1/(1 + 2,3) + … + bronceado -1 1/(1 + n(n + 1)) = bronceado -1 x
⇒ tan -1 (2 – 1)/(1 + 1,2) + tan -1 (3 – 2)/(1 + 2,3) + … + tan -1 (n + 1 – n)/(1 + n(n + 1)) = bronceado -1 x
⇒ (tan -1 2 – tan -1 1) + (tan -1 3 – tan -1 2) + … + (tan -1 (n + 1) – tan -1 n) = tan -1 x
⇒ bronceado -1 (n + 1) – bronceado -1 1 = bronceado -1 x
⇒ bronceado -1 n/(1 + (n + 1).1) = bronceado -1 x
⇒ bronceado -1 n/(n + 2) = bronceado -1 x
⇒x = n/(n + 2)
Pregunta 9: Si 2tan -1 (sen x) = tan -1 (2sec x) entonces resuelve para x.
Solución:
2tan -1 (sen x) = tan -1 (2seg x)
⇒ tan -1 (2sen x)/(1 – sen 2 x) = tan -1 (2/cos x)
⇒ (2sen x)/(1 – sen 2 x) = 2/cos x
⇒ sen x/cos 2 x = 1/cos x
⇒ sen x cos x = cos 2 x
⇒ sen x cos x – cos 2 x = 0
⇒ cos x(sen x – cos x) = 0
⇒ cos x = 0 o sen x – cos x = 0
⇒ cos x = cos /2 o tan x = tan /4
⇒ x = /2 o x = /4
Pero en x = /2 la ecuación dada no existe, por lo que x = /4 es la única solución.
Pregunta 10: Demuestre que cot -1 [ {√(1 + sen x) + √(1 – sen x)}/{√(1 + sen x) – √(1 – sen x)}] = x/2, x ∈ (0, /4)
Solución:
Sea x = 2y por lo tanto
LHS = cot -1 [{√(1+sen 2y) + √(1-sen 2y)}/{√(1+sen 2y) – √(1-sen 2y)}]
= cot -1 [{√(cos 2 y + sen 2 y + 2 sen y cos y) + √(cos 2 y + sen 2 y – 2 sen y cos y)}/{√(cos 2 y + sen 2 y + 2sen y cos y) – √(cos 2 y + sen 2 y – 2sen y cos y)} ]
= cot -1 [{√(cos y + sen y) 2 + √(cos y – sen y) 2 } / {√(cos y + sen y) 2 – √(cos y – sen y) 2 }]
= cot -1 [( cos y + sen y + cos y – sen y )/(cos y + sen y – cos y + sen y)]
= cot -1 (2cos y)/(2sen y)
= cuna -1 (cuna y)
= y
= x/2.
Publicación traducida automáticamente
Artículo escrito por akankshakumari92 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA