Implementación de BFS usando array de adyacencia

La búsqueda primero en amplitud (BFS) se ha discutido en este artículo que utiliza la lista de adyacencia para la representación gráfica. En este artículo, se utilizará la array de adyacencia para representar el gráfico.

Representación de array de adyacencia: en la representación de array de adyacencia de un gráfico, la array mat[][] de tamaño n*n (donde n es el número de vértices) representará los bordes del gráfico donde mat[i][j] = 1 representa que hay una arista entre los vértices i y j mientras que mat[i][j] = 0 representa que no hay arista entre los vértices i y j .
 

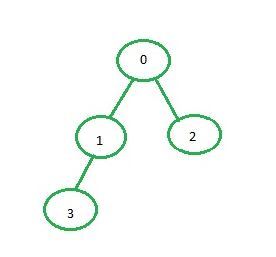
A continuación se muestra la representación de la array de adyacencia del gráfico que se muestra en la imagen de arriba: 

  0 1 2 3
0 0 1 1 0 
1 1 0 0 1 
2 1 0 0 0 
3 0 1 0 0

Ejemplos: 

Input: source = 0

Output: 0 1 2 3

Input: source = 1

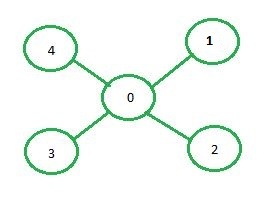
Output:1 0 2 3 4

Acercarse: 

• Cree una array de tamaño n*n donde cada elemento sea 0 y represente que no hay borde en el gráfico.
• Ahora, para cada borde del gráfico entre los vértices i y j, establezca mat[i][j] = 1.
• Después de que se haya creado y llenado la array de adyacencia, encuentre el recorrido BFS del gráfico como se describe en esta publicación.

A continuación se muestra la implementación del enfoque anterior: 

// C++ implementation of the approach
#include<bits/stdc++.h>
using namespace std;
 
vector<vector<int>> adj;
 
 
// function to add edge to the graph
void addEdge(int x,int y)
{
    adj[x][y] = 1;
    adj[y][x] = 1;
}
 
// Function to perform BFS on the graph
void bfs(int start)
{
    // Visited vector to so that
    // a vertex is not visited more than once
    // Initializing the vector to false as no
    // vertex is visited at the beginning
    vector<bool> visited(adj.size(), false);
    vector<int> q;
    q.push_back(start);
  
    // Set source as visited
    visited[start] = true;
  
    int vis;
    while (!q.empty()) {
        vis = q[0];
  
        // Print the current node
        cout << vis << " ";
        q.erase(q.begin());
  
        // For every adjacent vertex to the current vertex
        for (int i = 0; i < adj[vis].size(); i++) {
            if (adj[vis][i] == 1 && (!visited[i])) {
  
                // Push the adjacent node to the queue
                q.push_back(i);
  
                // Set
                visited[i] = true;
            }
        }
    }
}
  
// Driver code
int main()
{
  // number of vertices
  int v = 5;
 
 
  // adjacency matrix
  adj= vector<vector<int>>(v,vector<int>(v,0));
 
  addEdge(0,1);
  addEdge(0,2);
  addEdge(1,3);
   
  // perform bfs on the graph
  bfs(0);
}

// Java implementation of the approach
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
 
class GFG{
 
static class Graph
{
     
    // Number of vertex
    int v;
 
    // Number of edges
    int e;
 
    // Adjacency matrix
    int[][] adj;
 
    // Function to fill the empty
    // adjacency matrix
    Graph(int v, int e)
    {
        this.v = v;
        this.e = e;
         
        adj = new int[v][v];
        for(int row = 0; row < v; row++)
            Arrays.fill(adj[row], 0);
    }
     
    // Function to add an edge to the graph
    void addEdge(int start, int e)
    {
         
        // Considering a bidirectional edge
        adj[start][e] = 1;
        adj[e][start] = 1;
    }
 
    // Function to perform BFS on the graph
    void BFS(int start)
    {
         
        // Visited vector to so that
        // a vertex is not visited more than once
        // Initializing the vector to false as no
        // vertex is visited at the beginning
        boolean[] visited = new boolean[v];
        Arrays.fill(visited, false);
        List<Integer> q = new ArrayList<>();
        q.add(start);
 
        // Set source as visited
        visited[start] = true;
 
        int vis;
        while (!q.isEmpty())
        {
            vis = q.get(0);
 
            // Print the current node
            System.out.print(vis + " ");
            q.remove(q.get(0));
 
            // For every adjacent vertex to
            // the current vertex
            for(int i = 0; i < v; i++)
            {
                if (adj[vis][i] == 1 && (!visited[i]))
                {
                     
                    // Push the adjacent node to
                    // the queue
                    q.add(i);
 
                    // Set
                    visited[i] = true;
                }
            }
        }
    }
}
 
// Driver code
public static void main(String[] args)
{
     
    int v = 5, e = 4;
 
    // Create the graph
    Graph G = new Graph(v, e);
    G.addEdge(0, 1);
    G.addEdge(0, 2);
    G.addEdge(1, 3);
 
    G.BFS(0);
}
}
 
// This code is contributed by sanjeev2552

# Python3 implementation of the approach
class Graph:
     
    adj = []
 
    # Function to fill empty adjacency matrix
    def __init__(self, v, e):
         
        self.v = v
        self.e = e
        Graph.adj = [[0 for i in range(v)]
                        for j in range(v)]
 
    # Function to add an edge to the graph
    def addEdge(self, start, e):
         
        # Considering a bidirectional edge
        Graph.adj[start][e] = 1
        Graph.adj[e][start] = 1
 
    # Function to perform DFS on the graph
    def BFS(self, start):
         
        # Visited vector to so that a
        # vertex is not visited more than
        # once Initializing the vector to
        # false as no vertex is visited at
        # the beginning
        visited = [False] * self.v
        q = [start]
 
        # Set source as visited
        visited[start] = True
 
        while q:
            vis = q[0]
 
            # Print current node
            print(vis, end = ' ')
            q.pop(0)
             
            # For every adjacent vertex to
            # the current vertex
            for i in range(self.v):
                if (Graph.adj[vis][i] == 1 and
                      (not visited[i])):
                           
                    # Push the adjacent node
                    # in the queue
                    q.append(i)
                     
                    # set
                    visited[i] = True
 
# Driver code
v, e = 5, 4
 
# Create the graph
G = Graph(v, e)
G.addEdge(0, 1)
G.addEdge(0, 2)
G.addEdge(1, 3)
 
# Perform BFS
G.BFS(0)
 
# This code is contributed by ng24_7

// C# implementation of the approach
using System;
using System.Collections.Generic;
 
public class GFG{
 
  class Graph
  {
 
    // Number of vertex
    public int v;
 
    // Number of edges
    public int e;
 
    // Adjacency matrix
    public int[,] adj;
 
    // Function to fill the empty
    // adjacency matrix
    public Graph(int v, int e)
    {
      this.v = v;
      this.e = e;
 
      adj = new int[v,v];
      for(int row = 0; row < v; row++)
        for(int col = 0; col < v; col++)
          adj[row, col] = 0;
    }
 
    // Function to add an edge to the graph
    public void addEdge(int start, int e)
    {
 
      // Considering a bidirectional edge
      adj[start, e] = 1;
      adj[e, start] = 1;
    }
 
    // Function to perform BFS on the graph
    public void BFS(int start)
    {
 
      // Visited vector to so that
      // a vertex is not visited more than once
      // Initializing the vector to false as no
      // vertex is visited at the beginning
      bool[] visited = new bool[v];
      List<int> q = new List<int>();
      q.Add(start);
 
      // Set source as visited
      visited[start] = true;
 
      int vis;
      while (q.Count != 0)
      {
        vis = q[0];
 
        // Print the current node
        Console.Write(vis + " ");
        q.Remove(q[0]);
 
        // For every adjacent vertex to
        // the current vertex
        for(int i = 0; i < v; i++)
        {
          if (adj[vis,i] == 1 && (!visited[i]))
          {
 
            // Push the adjacent node to
            // the queue
            q.Add(i);
 
            // Set
            visited[i] = true;
          }
        }
      }
    }
  }
 
  // Driver code
  public static void Main(String[] args)
  {
 
    int v = 5, e = 4;
 
    // Create the graph
    Graph G = new Graph(v, e);
    G.addEdge(0, 1);
    G.addEdge(0, 2);
    G.addEdge(1, 3);
 
    G.BFS(0);
  }
}
 
// This code is contributed by shikhasingrajput

0 1 2 3

Complejidad temporal: O(N*N)
Espacio auxiliar: O(N)