El artículo anterior Optimización de enjambre de partículas: una descripción general habló sobre la inspiración de la optimización de enjambre de partículas (PSO), su modelado matemático y algoritmo. En este artículo implementaremos la optimización de enjambre de partículas (PSO) para dos funciones de aptitud 1) Función Rastrigin 2) Función Esfera. El algoritmo se ejecutará durante un número predefinido de iteraciones máximas e intentará encontrar el valor mínimo de estas funciones de aptitud.
Funciones de fitness
1) función rastrigina
La función Rastrigin es una función no convexa y se usa a menudo como un problema de prueba de rendimiento para algoritmos de optimización.
ecuación de la función:
![]()
![]()
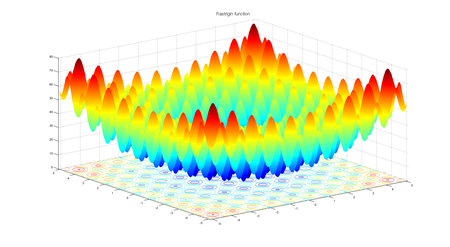
Fig1: función Rastrigin para 2 variables
Para un algoritmo de optimización, la función rastrigin es muy desafiante. Su comportamiento complejo hace que los algoritmos de optimización a menudo se atasquen en los mínimos locales. Tener muchas oscilaciones de coseno en el plano introduce el comportamiento complejo de esta función.
2) función de esfera
La función de esfera es una función estándar para evaluar el rendimiento de un algoritmo de optimización.
ecuación de la función:
![]()
![]()
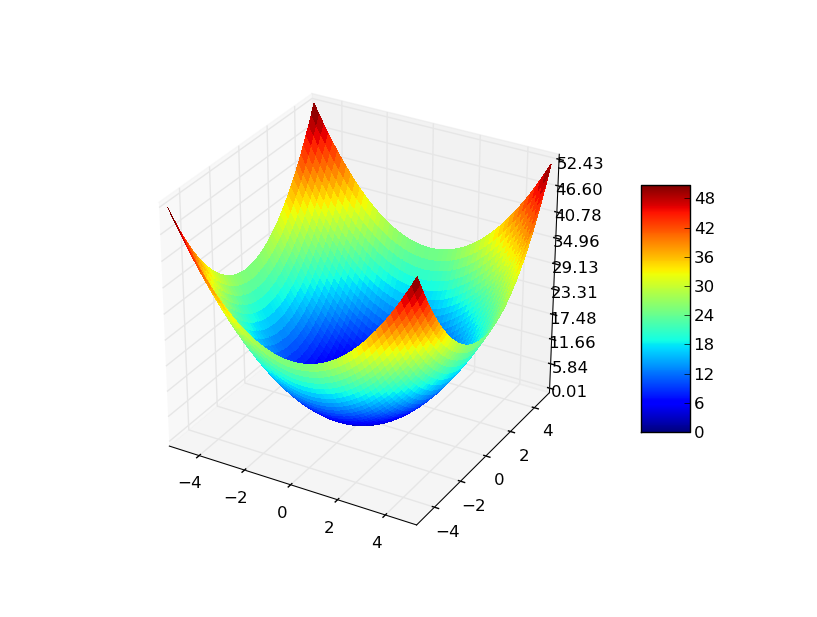
Fig2: Función de esfera para 2 variables
Elección de hiperparámetros
Parámetros del problema:
- Número de dimensiones ( d ) = 3
- Límite inferior ( minx ) = -10.0
- Límite superior ( maxx ) = 10.0
Hiperparámetros del algoritmo:
- Número de partículas ( N ) = 50
- Número máximo de iteraciones ( max_iter ) = 100
- coeficiente de inercia ( w ) = 0.729
- coeficiente cognitivo ( c1 ) = 1,49445
- coeficiente social ( c2 ) = 1.49445
Entradas
- función de fitness
- Parámetros del problema (mencionados anteriormente)
- Tamaño de la población ( N ) y número máximo de iteraciones ( max_iter )
- Hiperparámetros específicos del algoritmo ( w , c1 , c2 )
pseudocódigo
El pseudocódigo de la optimización del enjambre de partículas ya se describió en el artículo anterior . También se discutieron las estructuras de datos para almacenar la población de Swarm, así como una estructura de datos para almacenar datos específicos de partículas individuales.
Implementación
Python3
# python implementation of particle swarm optimization (PSO)
# minimizing rastrigin and sphere function
import random
import math # cos() for Rastrigin
import copy # array-copying convenience
import sys # max float
#-------fitness functions---------
# rastrigin function
def fitness_rastrigin(position):
fitnessVal = 0.0
for i in range(len(position)):
xi = position[i]
fitnessVal += (xi * xi) - (10 * math.cos(2 * math.pi * xi)) + 10
return fitnessVal
#sphere function
def fitness_sphere(position):
fitnessVal = 0.0
for i in range(len(position)):
xi = position[i]
fitnessVal += (xi*xi);
return fitnessVal;
#-------------------------
#particle class
class Particle:
def __init__(self, fitness, dim, minx, maxx, seed):
self.rnd = random.Random(seed)
# initialize position of the particle with 0.0 value
self.position = [0.0 for i in range(dim)]
# initialize velocity of the particle with 0.0 value
self.velocity = [0.0 for i in range(dim)]
# initialize best particle position of the particle with 0.0 value
self.best_part_pos = [0.0 for i in range(dim)]
# loop dim times to calculate random position and velocity
# range of position and velocity is [minx, max]
for i in range(dim):
self.position[i] = ((maxx - minx) *
self.rnd.random() + minx)
self.velocity[i] = ((maxx - minx) *
self.rnd.random() + minx)
# compute fitness of particle
self.fitness = fitness(self.position) # curr fitness
# initialize best position and fitness of this particle
self.best_part_pos = copy.copy(self.position)
self.best_part_fitnessVal = self.fitness # best fitness
# particle swarm optimization function
def pso(fitness, max_iter, n, dim, minx, maxx):
# hyper parameters
w = 0.729 # inertia
c1 = 1.49445 # cognitive (particle)
c2 = 1.49445 # social (swarm)
rnd = random.Random(0)
# create n random particles
swarm = [Particle(fitness, dim, minx, maxx, i) for i in range(n)]
# compute the value of best_position and best_fitness in swarm
best_swarm_pos = [0.0 for i in range(dim)]
best_swarm_fitnessVal = sys.float_info.max # swarm best
# computer best particle of swarm and it's fitness
for i in range(n): # check each particle
if swarm[i].fitness < best_swarm_fitnessVal:
best_swarm_fitnessVal = swarm[i].fitness
best_swarm_pos = copy.copy(swarm[i].position)
# main loop of pso
Iter = 0
while Iter < max_iter:
# after every 10 iterations
# print iteration number and best fitness value so far
if Iter % 10 == 0 and Iter > 1:
print("Iter = " + str(Iter) + " best fitness = %.3f" % best_swarm_fitnessVal)
for i in range(n): # process each particle
# compute new velocity of curr particle
for k in range(dim):
r1 = rnd.random() # randomizations
r2 = rnd.random()
swarm[i].velocity[k] = (
(w * swarm[i].velocity[k]) +
(c1 * r1 * (swarm[i].best_part_pos[k] - swarm[i].position[k])) +
(c2 * r2 * (best_swarm_pos[k] -swarm[i].position[k]))
)
# if velocity[k] is not in [minx, max]
# then clip it
if swarm[i].velocity[k] < minx:
swarm[i].velocity[k] = minx
elif swarm[i].velocity[k] > maxx:
swarm[i].velocity[k] = maxx
# compute new position using new velocity
for k in range(dim):
swarm[i].position[k] += swarm[i].velocity[k]
# compute fitness of new position
swarm[i].fitness = fitness(swarm[i].position)
# is new position a new best for the particle?
if swarm[i].fitness < swarm[i].best_part_fitnessVal:
swarm[i].best_part_fitnessVal = swarm[i].fitness
swarm[i].best_part_pos = copy.copy(swarm[i].position)
# is new position a new best overall?
if swarm[i].fitness < best_swarm_fitnessVal:
best_swarm_fitnessVal = swarm[i].fitness
best_swarm_pos = copy.copy(swarm[i].position)
# for-each particle
Iter += 1
#end_while
return best_swarm_pos
# end pso
#----------------------------
# Driver code for rastrigin function
print("\nBegin particle swarm optimization on rastrigin function\n")
dim = 3
fitness = fitness_rastrigin
print("Goal is to minimize Rastrigin's function in " + str(dim) + " variables")
print("Function has known min = 0.0 at (", end="")
for i in range(dim-1):
print("0, ", end="")
print("0)")
num_particles = 50
max_iter = 100
print("Setting num_particles = " + str(num_particles))
print("Setting max_iter = " + str(max_iter))
print("\nStarting PSO algorithm\n")
best_position = pso(fitness, max_iter, num_particles, dim, -10.0, 10.0)
print("\nPSO completed\n")
print("\nBest solution found:")
print(["%.6f"%best_position[k] for k in range(dim)])
fitnessVal = fitness(best_position)
print("fitness of best solution = %.6f" % fitnessVal)
print("\nEnd particle swarm for rastrigin function\n")
print()
print()
# Driver code for Sphere function
print("\nBegin particle swarm optimization on sphere function\n")
dim = 3
fitness = fitness_sphere
print("Goal is to minimize sphere function in " + str(dim) + " variables")
print("Function has known min = 0.0 at (", end="")
for i in range(dim-1):
print("0, ", end="")
print("0)")
num_particles = 50
max_iter = 100
print("Setting num_particles = " + str(num_particles))
print("Setting max_iter = " + str(max_iter))
print("\nStarting PSO algorithm\n")
best_position = pso(fitness, max_iter, num_particles, dim, -10.0, 10.0)
print("\nPSO completed\n")
print("\nBest solution found:")
print(["%.6f"%best_position[k] for k in range(dim)])
fitnessVal = fitness(best_position)
print("fitness of best solution = %.6f" % fitnessVal)
print("\nEnd particle swarm for sphere function\n")
Producción:
Begin particle swarm optimization on rastrigin function Goal is to minimize Rastrigin's function in 3 variables Function has known min = 0.0 at (0, 0, 0) Setting num_particles = 50 Setting max_iter = 100 Starting PSO algorithm Iter = 10 best fitness = 8.463 Iter = 20 best fitness = 4.792 Iter = 30 best fitness = 2.223 Iter = 40 best fitness = 0.251 Iter = 50 best fitness = 0.251 Iter = 60 best fitness = 0.061 Iter = 70 best fitness = 0.007 Iter = 80 best fitness = 0.005 Iter = 90 best fitness = 0.000 PSO completed Best solution found: ['0.000618', '0.000013', '0.000616'] fitness of best solution = 0.000151 End particle swarm for rastrigin function Begin particle swarm optimization on sphere function Goal is to minimize sphere function in 3 variables Function has known min = 0.0 at (0, 0, 0) Setting num_particles = 50 Setting max_iter = 100 Starting PSO algorithm Iter = 10 best fitness = 0.189 Iter = 20 best fitness = 0.012 Iter = 30 best fitness = 0.001 Iter = 40 best fitness = 0.000 Iter = 50 best fitness = 0.000 Iter = 60 best fitness = 0.000 Iter = 70 best fitness = 0.000 Iter = 80 best fitness = 0.000 Iter = 90 best fitness = 0.000 PSO completed Best solution found: ['0.000004', '-0.000001', '0.000007'] fitness of best solution = 0.000000 End particle swarm for sphere function
Referencias
Cita del trabajo de investigación: Kennedy, J. y Eberhart, R., 1995, noviembre. Optimización de Enjambre de partículas. En Actas de la conferencia internacional ICNN’95 sobre redes neuronales (Vol. 4, págs. 1942-1948). IEEE.
Inspiración de la implementación: https://fr.mathworks.com/matlabcentral/fileexchange/67429-a-simple-implementation-of-particle-swarm-optimization-pso-algorithm
Publicación traducida automáticamente
Artículo escrito por shaadk7865 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA