En este artículo, veremos la implementación de diferentes técnicas de regularización. Primero, comenzaremos con una regresión lineal múltiple. Para eso, requerimos el entorno python3 con sci-kit learn y pandas preinstalados. También podemos usar Google Collaboratory o cualquier otro entorno de notebook jupyter.
Primero, necesitamos importar algunos paquetes a nuestro entorno.
Python3
import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn import datasets from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression
Vamos a utilizar el conjunto de datos de predicción de casas de Boston. Este conjunto de datos está presente en el módulo de conjuntos de datos de la biblioteca sklearn (scikit-learn). Podemos importar este conjunto de datos de la siguiente manera.
Python3
# Loading pre-defined Boston Dataset boston_dataset = datasets.load_boston() print(boston_dataset.DESCR)
Producción:
Podemos concluir de la descripción anterior que tenemos 13 variables independientes y una variable dependiente (precio de la vivienda). Ahora necesitamos comprobar si hay una correlación entre la variable independiente y la dependiente. Podemos usar scatterplot/corrplot para esto.
Python3
# Generate scatter plot of independent vs Dependent variable
plt.style.use('ggplot')
fig = plt.figure(figsize = (18, 18))
for index, feature_name in enumerate(boston_dataset.feature_names):
ax = fig.add_subplot(4, 4, index + 1)
ax.scatter(boston_dataset.data[:, index], boston_dataset.target)
ax.set_ylabel('House Price', size = 12)
ax.set_xlabel(feature_name, size = 12)
plt.show()
El código anterior produce diagramas de dispersión de diferentes variables independientes con la variable objetivo como se muestra a continuación
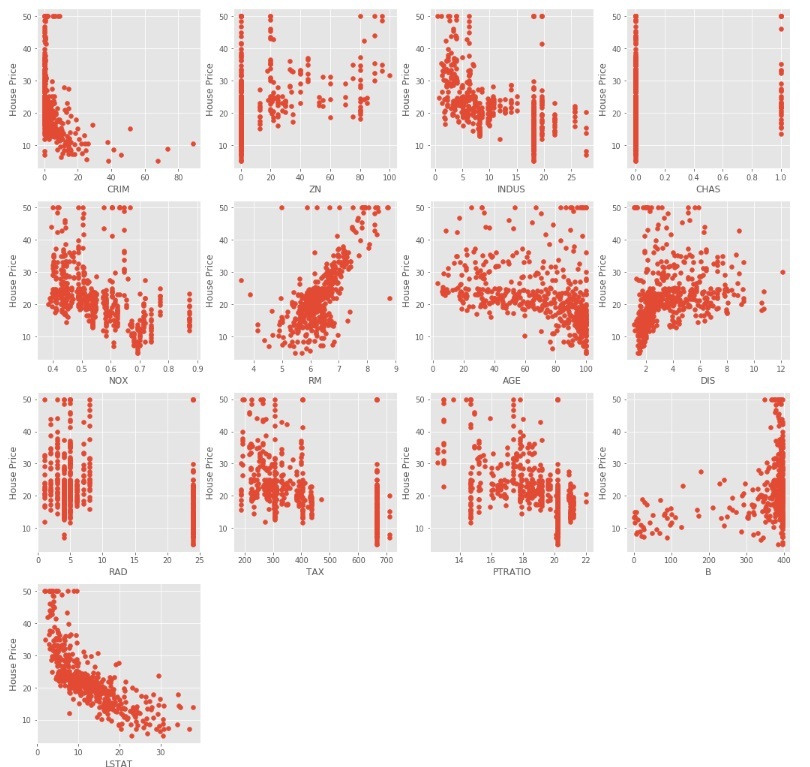
Podemos observar a partir de los diagramas de dispersión anteriores que algunas de las variables independientes no están muy correlacionadas (ya sea positiva o negativamente) con la variable objetivo. Estas variables conseguirán que sus coeficientes se reduzcan en la regularización.
Código: código de Python para preprocesar los datos.
Python3
# Load the dataset into Pandas Dataframe boston_pd = pd.DataFrame(boston_dataset.data) boston_pd.columns = boston_dataset.feature_names boston_pd_target = np.asarray(boston_dataset.target) boston_pd['House Price'] = pd.Series(boston_pd_target) # input X = boston_pd.iloc[:, :-1] #output Y = boston_pd.iloc[:, -1] print(boston_pd.head())
Ahora, aplicamos la división de prueba de tren para dividir el conjunto de datos en dos partes, una para entrenamiento y otra para prueba. Usaremos el 25% de los datos para las pruebas.
Python3
x_train, x_test, y_train, y_test = train_test_split(
boston_pd.iloc[:, :-1], boston_pd.iloc[:, -1],
test_size = 0.25)
print("Train data shape of X = % s and Y = % s : "%(
x_train.shape, y_train.shape))
print("Test data shape of X = % s and Y = % s : "%(
x_test.shape, y_test.shape))
Regresión múltiple (lineal)
Ahora es el momento adecuado para probar los modelos. Usaremos primero la regresión lineal múltiple. Entrenamos el modelo con datos de entrenamiento y calculamos el MSE en la prueba.
Python3
# Apply multiple Linear Regression Model
lreg = LinearRegression()
lreg.fit(x_train, y_train)
# Generate Prediction on test set
lreg_y_pred = lreg.predict(x_test)
# calculating Mean Squared Error (mse)
mean_squared_error = np.mean((lreg_y_pred - y_test)**2)
print("Mean squared Error on test set : ", mean_squared_error)
# Putting together the coefficient and their corresponding variable names
lreg_coefficient = pd.DataFrame()
lreg_coefficient["Columns"] = x_train.columns
lreg_coefficient['Coefficient Estimate'] = pd.Series(lreg.coef_)
print(lreg_coefficient)
Producción:
Tracemos un gráfico de barras de los coeficientes anteriores usando la biblioteca de trazado matplotlib.
Python3
# plotting the coefficient score
fig, ax = plt.subplots(figsize =(20, 10))
color =['tab:gray', 'tab:blue', 'tab:orange',
'tab:green', 'tab:red', 'tab:purple', 'tab:brown',
'tab:pink', 'tab:gray', 'tab:olive', 'tab:cyan',
'tab:orange', 'tab:green', 'tab:blue', 'tab:olive']
ax.bar(lreg_coefficient["Columns"],
lreg_coefficient['Coefficient Estimate'],
color = color)
ax.spines['bottom'].set_position('zero')
plt.style.use('ggplot')
plt.show()
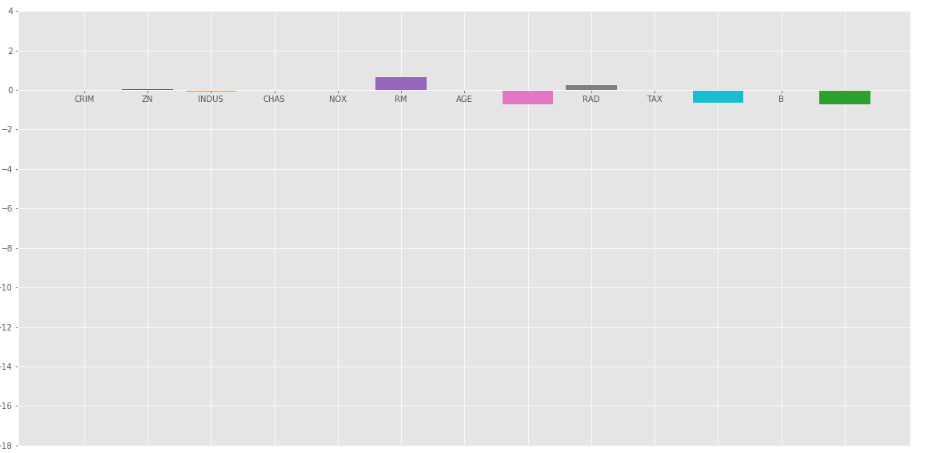
Producción:
Como podemos observar que muchas de las variables tienen un coeficiente insignificante, estos coeficientes no contribuyeron mucho al modelo y es necesario regular o incluso eliminar algunas de estas variables.
Ridge Regression:
Ridge Regression agregó un término en la función de error de mínimos cuadrados ordinarios que regulariza el valor de los coeficientes de las variables. Este término es la suma de los cuadrados del coeficiente multiplicado por el parámetro. El motivo de agregar este término es penalizar la variable correspondiente a ese coeficiente poco correlacionada con la variable objetivo. Este término se denomina regularización L 2 .
Código: código de Python para usar la regresión de Ridge
Python3
# import ridge regression from sklearn library from sklearn.linear_model import Ridge # Train the model ridgeR = Ridge(alpha = 1) ridgeR.fit(x_train, y_train) y_pred = ridgeR.predict(x_test) # calculate mean square error mean_squared_error_ridge = np.mean((y_pred - y_test)**2) print(mean_squared_error_ridge) # get ridge coefficient and print them ridge_coefficient = pd.DataFrame() ridge_coefficient["Columns"]= x_train.columns ridge_coefficient['Coefficient Estimate'] = pd.Series(ridgeR.coef_) print(ridge_coefficient)
Salida: el valor del error MSE y el marco de datos con coeficientes de cresta.
El gráfico de barras de los datos anteriores es:
Regresión de cresta en 
= 1
En el gráfico anterior tomamos = 1.
Veamos otro gráfico de barras con = 10
Regresión de cresta en = 10
Como podemos observar en los gráficos anteriores, eso ayuda a regularizar el coeficiente y hacer que converjan más rápido.
Tenga en cuenta que los gráficos anteriores pueden ser engañosos en el sentido de que muestran que algunos de los coeficientes se vuelven cero. En Ridge Regularization, los coeficientes nunca pueden ser 0, son demasiado pequeños para observarlos en los gráficos anteriores.
Regresión de lazo: La regresión
de lazo es similar a la regresión de Ridge, excepto que aquí agregamos el valor absoluto medio de los coeficientes en lugar del valor cuadrático medio. A diferencia de la regresión de Ridge, la regresión de Lasso puede eliminar completamente la variable al reducir el valor de su coeficiente a 0. El nuevo término que agregamos a Mínimos cuadrados ordinarios (OLS) se llama Regularización L 1 .
Código: código de Python que implementa la regresión de Lasso
Python3
# import Lasso regression from sklearn library
from sklearn.linear_model import Lasso
# Train the model
lasso = Lasso(alpha = 1)
lasso.fit(x_train, y_train)
y_pred1 = lasso.predict(x_test)
# Calculate Mean Squared Error
mean_squared_error = np.mean((y_pred1 - y_test)**2)
print("Mean squared error on test set", mean_squared_error)
lasso_coeff = pd.DataFrame()
lasso_coeff["Columns"] = x_train.columns
lasso_coeff['Coefficient Estimate'] = pd.Series(lasso.coef_)
print(lasso_coeff)
Salida: el valor del error de MSE y el marco de datos con coeficientes de Lasso.
Regresión de lazo con = 1
El gráfico de barras de los coeficientes anteriores:
Regresión de lazo con =1
La regresión de Lasso dio el mismo resultado que dio la regresión de cresta, cuando aumentamos el valor de . Veamos otro gráfico en = 10.
Red elástica:
en Regularización neta elástica, agregamos los dos términos de L 1 y L 2 para obtener la función de pérdida final. Esto nos lleva a reducir la siguiente función de pérdida: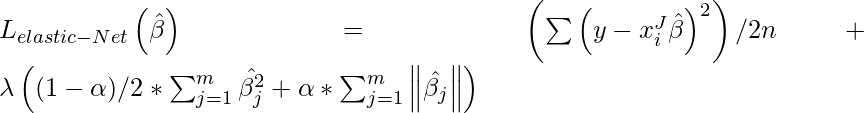 
donde está entre 0 y 1. cuando = 1, reduce el término de penalización a L 1 penalización y si = 0, reduce ese término a L 2
penalización.
Código: código de Python que implementa Elastic Net
Python3
# import model
from sklearn.linear_model import ElasticNet
# Train the model
e_net = ElasticNet(alpha = 1)
e_net.fit(x_train, y_train)
# calculate the prediction and mean square error
y_pred_elastic = e_net.predict(x_test)
mean_squared_error = np.mean((y_pred_elastic - y_test)**2)
print("Mean Squared Error on test set", mean_squared_error)
e_net_coeff = pd.DataFrame()
e_net_coeff["Columns"] = x_train.columns
e_net_coeff['Coefficient Estimate'] = pd.Series(e_net.coef_)
e_net_coeff
Producción:
Gráfico de barras de los coeficientes anteriores:
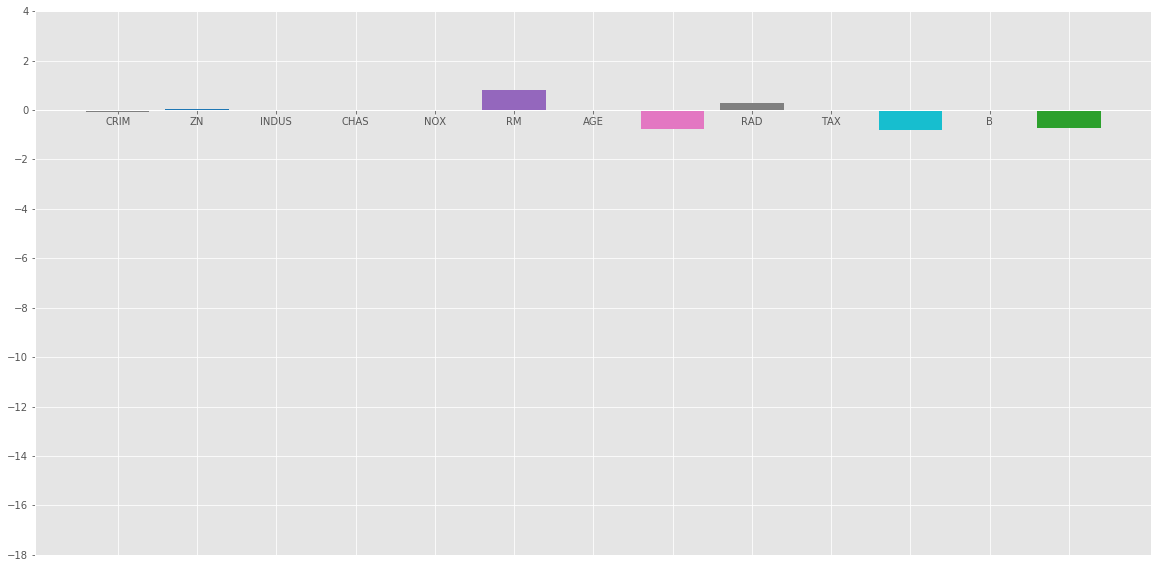
Conclusión:
del análisis anterior podemos llegar a la siguiente conclusión sobre los diferentes métodos de regularización:
- La regularización se usa para reducir la dependencia de cualquier variable independiente en particular agregando el término de penalización a la función de pérdida. Este término evita que los coeficientes de las variables independientes tomen valores extremos.
- Ridge Regression agrega el término de penalización de regularización L 2 a la función de pérdida. Este término reduce los coeficientes pero no los convierte en 0 y, por lo tanto, no elimina por completo ninguna variable independiente. Se puede utilizar para medir el impacto de las diferentes variables independientes.
- Lasso Regression agrega L 1 término de penalización de regularización a la función de pérdida. Este término reduce los coeficientes y los convierte en 0, por lo que elimina completamente la variable independiente correspondiente. Se puede utilizar para la selección de funciones, etc.
- Elastic Net es una combinación de las dos regularizaciones anteriores. Contiene tanto la L 1 como la L 2 como su término de sanción. Funciona mejor que Ridge and Lasso Regression para la mayoría de los casos de prueba.