Imprima todas las rutas posibles en un DAG desde el vértice cuyo grado de entrada sea 0

Dado un gráfico acíclico dirigido (DAG), que tiene N vértices y M aristas, la tarea es imprimir todas las rutas a partir del vértice cuyo grado de entrada sea cero. 

El grado interior de un vértice es el número total de aristas entrantes a un vértice. 
 

Ejemplo:  

Entrada: N = 6, bordes[] = {{5, 0}, {5, 2}, {4, 0}, {4, 1}, {2, 3}, {3, 1}} 
Salida: Todo caminos posibles: 
4 0 
4 1 
5 0 
5 2 3 1 
Explicación: 
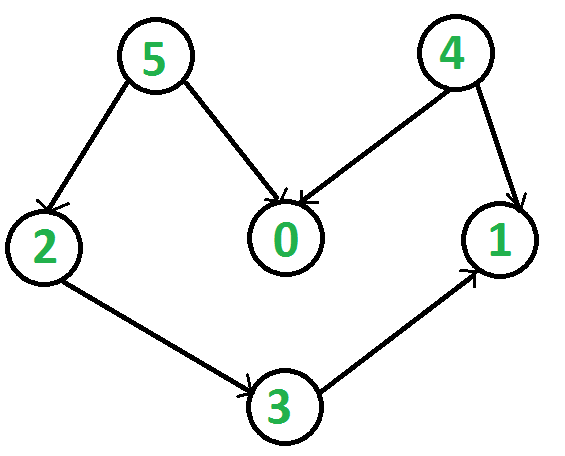
El gráfico dado se puede representar como: 
 

Hay dos vértices cuyo grado de entrada es cero, es decir, los vértices 5 y 4, después de explorar estos vértices obtuvimos el siguiente camino: 
4 -> 0 
4 -> 1 
5 -> 0 
5 -> 2 -> 3 -> 1 

Entrada: N = 6, bordes[] = {{0, 5}} 
Salida: Todos los caminos posibles: 
0 5 
Explicación: 
Solo habrá un camino posible en el gráfico. 

Acercarse:  

1. Cree una array booleana indeg0 que almacene un valor verdadero para todos aquellos vértices cuyo grado de entrada sea cero.
2. Aplicar DFS en todos aquellos vértices cuyo grado de entrada sea 0.
3. Imprime todas las rutas desde un vértice cuyo grado de entrada es 0 hasta un vértice cuyos grados de salida son cero.

Ilustración: 
Para el gráfico anterior: 
indeg0[] = {False, False, False, False, True, True} 
Dado que indeg[4] = True, la aplicación de DFS en el vértice 4 y la impresión de todas las rutas que terminan en 0 fuera del vértice son las siguientes : 
4 -> 0 
4 -> 1 
También indeg[5] = True, por lo que aplicar DFS en el vértice 5 e imprimir todas las rutas que terminan en 0 fuera del vértice son las siguientes: 
5 -> 0 
5 -> 2 -> 3 -> 1 
 

Aquí está la implementación del enfoque anterior: 

// C++ program to print
// all possible paths in a DAG
 
#include <bits/stdc++.h>
using namespace std;
 
vector<int> path;
 
vector<bool> indeg0, outdeg0;
 
vector<vector<int> > adj;
 
vector<bool> visited;
 
// Recursive function to print all paths
void dfs(int s)
{
    // Append the node in path
    // and set visited
    path.push_back(s);
    visited[s] = true;
 
    //  Path started with a node
    //  having in-degree 0 and
    //  current node has out-degree 0,
    //  print current path
    if (outdeg0[s] && indeg0[path[0]]) {
        for (auto x : path)
            cout << x << " ";
        cout << '\n';
    }
 
    for (auto node : adj[s]) {
        if (!visited[node])
            dfs(node);
    }
 
    path.pop_back();
    visited[s] = false;
}
 
void print_all_paths(int n)
{
    for (int i = 0; i < n; i++) {
        // for each node with in-degree 0
        // print all possible paths
        if (indeg0[i] && !adj[i].empty()) {
            dfs(i);
        }
    }
}
 
// Driver Code
int main()
{
    int n;
    n = 6;
 
    // set all nodes unvisited
    visited = vector<bool>(n, false);
 
    // adjacency list for nodes
    adj = vector<vector<int> >(n);
 
    // indeg0 and outdeg0 arrays
    indeg0 = vector<bool>(n, true);
    outdeg0 = vector<bool>(n, true);
 
    // edges
    vector<pair<int, int> > edges
        = { { 5, 0 }, { 5, 2 }, { 2, 3 },
            { 4, 0 }, { 4, 1 }, { 3, 1 } };
 
    for (int i = 0; i < edges.size(); i++) {
        int u = edges[i].first;
        int v = edges[i].second;
 
        adj[u].push_back(v);
 
        // set indeg0[v] <- false
        indeg0[v] = false;
 
        // set outdeg0[u] <- false
        outdeg0[u] = false;
    }
    cout << "All possible paths:\n";
    print_all_paths(n);
    return 0;
}

# Python program to print all
# possible paths in a DAG
 
# Recursive function to print all paths
def dfs(s):
    # Append the node in path
    # and set visited
    path.append(s)
    visited[s] = True
 
    # Path started with a node
    # having in-degree 0 and
    # current node has out-degree 0,
    # print current path
    if outdeg0[s] and indeg0[path[0]]:
        print(*path)
 
    # Recursive call to print all paths
    for node in adj[s]:
        if not visited[node]:
            dfs(node)
 
    # Remove node from path
    # and set unvisited
    path.pop()
    visited[s] = False
 
 
def print_all_paths(n):
    for i in range(n):
 
        # for each node with in-degree 0
        # print all possible paths
        if indeg0[i] and adj[i]:
            path = []
            visited = [False] * (n + 1)
            dfs(i)
 
 
# Driver code
from collections import defaultdict
 
n = 6
# set all nodes unvisited
visited = [False] * (n + 1)
path = []
 
# edges = (a, b): a -> b
edges = [(5, 0), (5, 2), (2, 3),
         (4, 0), (4, 1), (3, 1)]
 
# adjacency list for nodes
adj = defaultdict(list)
 
# indeg0 and outdeg0 arrays
indeg0 = [True]*n
outdeg0 = [True]*n
 
for edge in edges:
    u, v = edge[0], edge[1]
    # u -> v
    adj[u].append(v)
 
    # set indeg0[v] <- false
    indeg0[v] = False
 
    # set outdeg0[u] <- false
    outdeg0[u] = False
 
print('All possible paths:')
print_all_paths(n)

All possible paths:
4 0
4 1
5 0
5 2 3 1

Complejidad Temporal: O (N + E) ²  
Espacio Auxiliar: O (N)