Imprime todas las permutaciones de longitud L usando los elementos de un arreglo | Iterativo

Dada una array de elementos únicos , tenemos que encontrar todas las permutaciones de longitud L usando los elementos de la array. Se permite la repetición de elementos.
Ejemplos: 

Entrada: arr = { 1, 2 }, L=3 
Salida: 
111 
211 
121 
221 
112 
212 
122 
222
Entrada: arr = { 1, 2, 3 }, L=2 
Salida: 
11 
21 
31 
12 
22 
32 
13 
23 
33 
 

Acercarse: 

• Para formar una secuencia de longitud L con N número de elementos, se sabe que el i-ésimo elemento de la secuencia se puede llenar de N formas. Entonces habrá 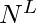 secuencias
• Ejecutaremos un ciclo de 0 a 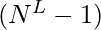 , para cada i convertiremos i de base 10 a base N . Los dígitos del número convertido representarán los índices de la array.
• Podemos imprimir todas las 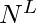 secuencias de esta manera.

A continuación se muestra la implementación del enfoque: 

// C++ implementation
#include <bits/stdc++.h>
using namespace std;
 
// Convert the number to Lth
// base and print the sequence
void convert_To_Len_th_base(int n,
                            int arr[],
                            int len,
                            int L)
{
    // Sequence is of length L
    for (int i = 0; i < L; i++) {
        // Print the ith element
        // of sequence
        cout << arr[n % len];
        n /= len;
    }
    cout << endl;
}
 
// Print all the permuataions
void print(int arr[],
           int len,
           int L)
{
    // There can be (len)^l
    // permutations
    for (int i = 0; i < (int)pow(len, L); i++) {
        // Convert i to len th base
        convert_To_Len_th_base(i, arr, len, L);
    }
}
 
// Driver code
int main()
{
    int arr[] = { 1, 2, 3 };
    int len = sizeof(arr) / sizeof(arr[0]);
    int L = 2;
 
    // function call
    print(arr, len, L);
 
    return 0;
}

// Java implementation for above approach
import java.io.*;
 
class GFG
{
     
// Convert the number to Lth
// base and print the sequence
static void convert_To_Len_th_base(int n, int arr[],
                                   int len, int L)
{
    // Sequence is of length L
    for (int i = 0; i < L; i++)
    {
        // Print the ith element
        // of sequence
        System.out.print(arr[n % len]);
        n /= len;
    }
    System.out.println();
}
 
// Print all the permuataions
static void print(int arr[], int len, int L)
{
    // There can be (len)^l
    // permutations
    for (int i = 0;
             i < (int)Math.pow(len, L); i++)
    {
        // Convert i to len th base
        convert_To_Len_th_base(i, arr, len, L);
    }
}
 
// Driver code
public static void main (String[] args)
{
    int arr[] = { 1, 2, 3 };
    int len = arr.length;
    int L = 2;
     
    // function call
    print(arr, len, L);
}
}
 
// This code is contributed by ajit.

# Python3 implementation for the above approach
 
# Convert the number to Lth
# base and print the sequence
def convert_To_Len_th_base(n, arr, Len, L):
     
    # Sequence is of Length L
    for i in range(L):
         
        # Print the ith element
        # of sequence
        print(arr[n % Len], end = "")
        n //= Len
    print()
 
# Print all the permuataions
def printf(arr, Len, L):
     
    # There can be (Len)^l permutations
    for i in range(pow(Len, L)):
         
        # Convert i to Len th base
        convert_To_Len_th_base(i, arr, Len, L)
 
# Driver code
arr = [1, 2, 3]
Len = len(arr)
L = 2
 
# function call
printf(arr, Len, L)
 
# This code is contributed by Mohit Kumar

// C# implementation for above approach
using System;
 
class GFG
{
     
// Convert the number to Lth
// base and print the sequence
static void convert_To_Len_th_base(int n, int []arr,
                                   int len, int L)
{
    // Sequence is of length L
    for (int i = 0; i < L; i++)
    {
        // Print the ith element
        // of sequence
        Console.Write(arr[n % len]);
        n /= len;
    }
    Console.WriteLine();
}
 
// Print all the permuataions
static void print(int []arr, int len, int L)
{
    // There can be (len)^l
    // permutations
    for (int i = 0;
            i < (int)Math.Pow(len, L); i++)
    {
        // Convert i to len th base
        convert_To_Len_th_base(i, arr, len, L);
    }
}
 
// Driver code
public static void Main (String[] args)
{
    int []arr = { 1, 2, 3 };
    int len = arr.Length;
    int L = 2;
     
    // function call
    print(arr, len, L);
}
}
 
// This code is contributed by Rajput-Ji

<script>
// Javascript implementation
 
// Convert the number to Lth
// base and print the sequence
function convert_To_Len_th_base( n, arr, len, L)
{
    // Sequence is of length L
    for ( i = 0; i < L; i++) {
        // Print the ith element
        // of sequence
        document.write(parseInt(arr[n % len]));
        n = parseInt(n / len);
    }
   document.write("<br>");
}
 
// Print all the permuataions
function print( arr, len, L)
{
    // There can be (len)^l
    // permutations
    for (var i = 0; i < parseInt(Math.pow(len, L)); i++) {
        // Convert i to len th base
        convert_To_Len_th_base(i, arr, len, L);
    }
}
 
var arr = [ 1, 2, 3 ];
var len = arr.length;
var L = 2;
 
// function call
print(arr, len, L);
 
//This code is contributed by SoumikModnal
</script>

11
21
31
12
22
32
13
23
33

Complejidad de tiempo: O(L*len ^L ), ya que estamos usando un ciclo para recorrer pow(len,L) tiempos y en cada recorrido, estamos llamando a la función convert_To_Len_th_base que costará O(L). Donde L es el número de elementos de la array.
Espacio auxiliar: O(1), ya que no estamos utilizando ningún espacio adicional.