Imprime todas las palabras posibles de los dígitos del teléfono

Antes de la llegada de los teclados QWERTY, los textos y los números se colocaban en la misma tecla. Por ejemplo, 2 tiene «ABC» si queremos escribir algo que comience con ‘A’ necesitamos escribir la tecla 2 una vez. Si quisiéramos escribir ‘B’, presione la tecla 2 dos veces y tres veces para escribir ‘C’. A continuación se muestra una imagen de dicho teclado.

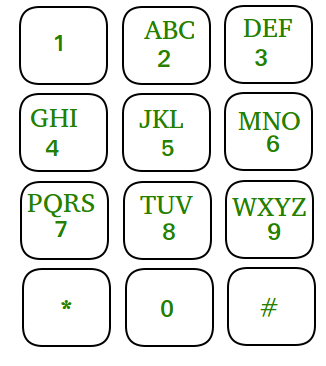
Dado un teclado como se muestra en el diagrama, y ​​un número de n dígitos, enumere todas las palabras que son posibles presionando estos números.

Ejemplo: 

Input number: 234
Output:
adg adh adi aeg aeh aei afg afh 
afi bdg bdh bdi beg beh bei bfg 
bfh bfi cdg cdh cdi ceg ceh cei 
cfg cfh cfi

Explanation: All possible words which can be 
formed are (Alphabetical order):
adg adh adi aeg aeh aei afg afh 
afi bdg bdh bdi beg beh bei bfg 
bfh bfi cdg cdh cdi ceg ceh cei 
cfg cfh cfi
If 2 is pressed then the alphabet
can be a, b, c, 
Similarly, for 3, it can be 
d, e, f, and for 4 can be g, h, i. 

Input number: 5
Output: j k l
Explanation: All possible words which can be 
formed are (Alphabetical order):
j, k, l, only these three alphabets 
can be written with j, k, l.

Planteamiento: Se puede observar que cada dígito puede representar de 3 a 4 alfabetos diferentes (aparte del 0 y 1). Así que la idea es formar una función recursiva. Luego mapee el número con su string de alfabetos probables, es decir, 2 con «abc», 3 con «def», etc. Ahora la función recursiva probará todos los alfabetos, mapeados al dígito actual en orden alfabético, y nuevamente llamará a la función recursiva para el siguiente dígito y pasará la string de salida actual.

Ejemplo: 

If the number is 23,

Then for 2, the alphabets are a, b, c
So 3 recursive function will be called 
with output string as a, b, c respectively 
and for 3 there are 3 alphabets d, e, f
So, the output will be ad, ae and af for 
the recursive function with output string.
Similarly, for b and c, the output will be: 
bd, be, bf and cd, ce, cf respectively.

Algoritmo:  

1. Asigne el número con su string de alfabetos probables, es decir, 2 con «abc», 3 con «def», etc.
2. Cree una función recursiva que tome los siguientes parámetros, string de salida, array de números, índice actual y longitud de la array de números
3. Si el índice actual es igual a la longitud de la array de números, imprima la string de salida.
4. Extraiga la string en el dígito [índice_actual] del mapa, donde el dígito es la array de números de entrada.
5. Ejecute un ciclo para recorrer la string de principio a fin
6. Para cada índice, vuelva a llamar a la función recursiva con la string de salida concatenada con el i-ésimo carácter de la string y el índice_actual + 1.

Implementación: tenga en cuenta que el número de entrada se representa como una array para simplificar el código. 

// C++ program for the above approach
  
#include <bits/stdc++.h>
using namespace std;
  
// Function to find all possible combinations by
// replacing key's digits with characters of the 
// corresponding list
void findCombinations(vector<char> keypad[], 
                      int input[], string res, int index, int n)
{
    // If processed every digit of key, print result
    if (index == n) {
        cout << res << " ";
        return;
    }
  
    // Stores current digit
    int digit = input[index];
  
    // Size of the list corresponding to current digit
    int len = keypad[digit].size();
  
    // One by one replace the digit with each character in the
    // corresponding list and recur for next digit
    for (int i = 0; i < len; i++) {
        findCombinations(keypad, input, res + keypad[digit][i], index + 1, n);
    }
}
  
// Driver Code
int main()
{
    // Given mobile keypad
    vector<char> keypad[] =
    {
        {}, {},        // 0 and 1 digit don't have any characters associated
        { 'a', 'b', 'c' },
        { 'd', 'e', 'f' },
        { 'g', 'h', 'i' },
        { 'j', 'k', 'l' },
        { 'm', 'n', 'o' },
        { 'p', 'q', 'r', 's'},
        { 't', 'u', 'v' },
        { 'w', 'x', 'y', 'z'}
    };
  
    // Given input array
    int input[] = { 2, 3, 4 };
    
    // Size of the array
    int n = sizeof(input)/sizeof(input[0]);
  
    // Function call to find all combinations
    findCombinations(keypad, input, string(""), 0, n );
  
    return 0;
}

#include <stdio.h>
#include <string.h>
  
// hashTable[i] stores all characters that correspond to
// digit i in phone
const char hashTable[10][5]
    = { "",    "",    "abc",  "def", "ghi",
        "jkl", "mno", "pqrs", "tuv", "wxyz" };
  
// A recursive function to print all possible words that can
// be obtained by input number[] of size n.  The output
// words are one by one stored in output[]
void printWordsUtil(int number[], int curr_digit,
                    char output[], int n)
{
    // Base case, if current output word is prepared
    int i;
    if (curr_digit == n) {
        printf("%s ", output);
        return;
    }
  
    // Try all 3 possible characters for current digit in
    // number[] and recur for remaining digits
    for (i = 0; i < strlen(hashTable[number[curr_digit]]);
         i++) {
        output[curr_digit]
            = hashTable[number[curr_digit]][i];
        printWordsUtil(number, curr_digit + 1, output, n);
        if (number[curr_digit] == 0
            || number[curr_digit] == 1)
            return;
    }
}
  
// A wrapper over printWordsUtil().  It creates an output
// array and calls printWordsUtil()
void printWords(int number[], int n)
{
    char result[n + 1];
    result[n] = '\0';
    printWordsUtil(number, 0, result, n);
}
  
// Driver program
int main(void)
{
    int number[] = { 2, 3, 4 };
    int n = sizeof(number) / sizeof(number[0]);
    printWords(number, n);
    return 0;
}

// Java program to implement the
// above approach
import java.util.*;
import java.lang.*;
import java.io.*;
class NumberPadString{
       
static Character[][] numberToCharMap;
  
private static List<String> printWords(int[] numbers, 
                                       int len, 
                                       int numIndex, 
                                       String s)
{
  if(len == numIndex)
  {
    return new ArrayList<>(Collections.singleton(s));
  }
    
  List<String> stringList = new ArrayList<>();
    
  for(int i = 0; 
          i < numberToCharMap[numbers[numIndex]].length; i++)
  {
    String sCopy = 
           String.copyValueOf(s.toCharArray());
    sCopy = sCopy.concat(
            numberToCharMap[numbers[numIndex]][i].toString());
    stringList.addAll(printWords(numbers, len, 
                                 numIndex + 1, 
                                 sCopy));
  }
  return stringList;
}
      
private static void printWords(int[] numbers)
{
  generateNumberToCharMap();
  List<String> stringList = 
       printWords(numbers, numbers.length, 0, "");
  stringList.stream().forEach(System.out :: println);
}
  
private static void generateNumberToCharMap()
{
  numberToCharMap = new Character[10][5];
  numberToCharMap[0] = new Character[]{'\0'};
  numberToCharMap[1] = new Character[]{'\0'};
  numberToCharMap[2] = new Character[]{'a','b','c'};
  numberToCharMap[3] = new Character[]{'d','e','f'};
  numberToCharMap[4] = new Character[]{'g','h','i'};
  numberToCharMap[5] = new Character[]{'j','k','l'};
  numberToCharMap[6] = new Character[]{'m','n','o'};
  numberToCharMap[7] = new Character[]{'p','q','r','s'};
  numberToCharMap[8] = new Character[]{'t','u','v'};
  numberToCharMap[9] = new Character[]{'w','x','y','z'};
}
  
// Driver code  
public static void main(String[] args) 
{
  int number[] = {2, 3, 4};
  printWords(number);
}
}
  
// This code is contributed by ankit pachori 1

# hashTable[i] stores all characters
# that correspond to digit i in phone
hashTable = ["", "", "abc", "def", "ghi", "jkl",
             "mno", "pqrs", "tuv", "wxyz"]
  
# A recursive function to print all
# possible words that can be obtained
# by input number[] of size n. The
# output words are one by one stored
# in output[]
  
  
def printWordsUtil(number, curr, output, n):
    if(curr == n):
        print(output)
        return
  
    # Try all 3 possible characters
    # for current digit in number[]
    # and recur for remaining digits
    for i in range(len(hashTable[number[curr]])):
        output.append(hashTable[number[curr]][i])
        printWordsUtil(number, curr + 1, output, n)
        output.pop()
        if(number[curr] == 0 or number[curr] == 1):
            return
  
# A wrapper over printWordsUtil().
# It creates an output array and
# calls printWordsUtil()
  
  
def printWords(number, n):
    printWordsUtil(number, 0, [], n)
  
  
# Driver function
if __name__ == '__main__':
    number = [2, 3, 4]
    n = len(number)
    printWords(number, n)
  
# This code is contributed by prajmsidc

using System;
/*
  C# Program for
  Print all possible words from phone digits
*/
public class GFG {
    // Function to find all possible combinations by
    // replacing key's digits with characters of the
    // corresponding list
    static void findCombinations(String[] keypad,
                                 int[] input, String result,
                                 int index, int n)
    {
        // If processed every digit of key, print result
        if (index == n) {
            Console.Write(result + "\t");
            return;
        }
  
        // Stores current digit
        int digit = input[index];
        // Size of the list corresponding to current digit
        int len = keypad[digit].Length;
        // One by one replace the digit with each character
        // in the corresponding list and recur for next
        // digit
        for (int i = 0; i < len; i++) {
            findCombinations(keypad, input,
                             result + keypad[digit][i],
                             index + 1, n);
        }
    }
  
    public static void Main(String[] args)
    {
        // Keypad word of number of (1 to 9)
        // 0 and 1 digit don't have any characters
        // associated
        String[] keypad
            = { "",    "",    "abc",  "def", "ghi",
                "jkl", "mno", "pqrs", "tuv", "wxyz" };
        String result = "";
        // Given input array
        int[] input = { 2, 3, 4 };
        // Size of the array
        int n = input.Length;
        // Function call to find all combinations
        findCombinations(keypad, input, result, 0, n);
    }
}
// This code is contributed by Aarti_Rathi

<script>
  
// Javascript program to implement the
// above approach
let hashTable = [ "", "", "abc", "def", "ghi", "jkl",
                  "mno", "pqrs", "tuv", "wxyz" ];
                    
// A recursive function to print all possible 
// words that can be obtained by input number[]
// of size n. The output words are one by one 
// stored in output[]
function printWordsUtil(number, curr, output, n)
{
      
    // Base case, if current output
    // word is prepared
    if (curr == n)
      {
        document.write(output.join("") + "<br>")
        return;
      }
        
      // Try all 3 possible characters for current
      // digit in number[] and recur for remaining digits
    for(let i = 0; 
            i < hashTable[number[curr]].length; 
            i++)
    {
        output.push(hashTable[number[curr]][i]);
        printWordsUtil(number, curr + 1, output, n);
          
        output.pop();
          
        if(number[curr] == 0 || number[curr] == 1)
            return
    }
}
  
// A wrapper over printWordsUtil(). It creates 
// an output array and calls printWordsUtil()
function printWords(numbers, n)
{
    printWordsUtil(number, 0, [], n);
}
  
// Driver code 
let number = [ 2, 3, 4 ];
let n = number.length;
  
printWords(number, n);
  
// This code is contributed by avanitrachhadiya2155
  
</script>

adg adh adi aeg aeh aei afg afh afi bdg bdh bdi beg beh
 bei bfg bfh bfi cdg cdh cdi ceg ceh cei cfg cfh cfi 

Análisis de Complejidad:  

• Complejidad de tiempo: O(4 ⁿ ), donde n es un número de dígitos en el número de entrada. 
  Cada dígito de un número tiene 3 o 4 letras, por lo que se puede decir que cada dígito tiene 4 letras como opciones. Si hay n dígitos, entonces hay 4 opciones para el primer dígito y para cada alfabeto del primer dígito hay 4 opciones en el segundo dígito, es decir, por cada recursión se llaman 4 recursiones más (si no coincide con el caso base) . Entonces la complejidad del tiempo es O(4 ⁿ ).
• Complejidad espacial: O(1). 
  Como no se necesita espacio adicional.