Dado un gráfico y un vértice de origen en el gráfico, encuentre los caminos más cortos desde el origen hasta todos los vértices en el gráfico dado.
Hemos discutido el algoritmo de ruta más corta de Dijkstra en las publicaciones a continuación.
- El camino más corto de Dijkstra para la representación de arrays de adyacencia
- La ruta más corta de Dijkstra para la representación de listas de adyacencia
Las implementaciones discutidas anteriormente solo encuentran distancias más cortas, pero no imprimen rutas. En este post se discute la impresión de caminos.
For example, consider below graph and source as 0,
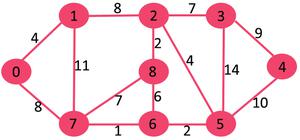
Gráfico utilizado en el problema
La salida para el gráfico se ve así: –
Vertex Distance Path 0 -> 1 4 0 1 0 -> 2 12 0 1 2 0 -> 3 19 0 1 2 3 0 -> 4 21 0 7 6 5 4 0 -> 5 11 0 7 6 5 0 -> 6 9 0 7 6 0 -> 7 8 0 7 0 -> 8 14 0 1 2 8
La idea es crear una array separada parent[]. El valor de parent[v] para un vértice v almacena el vértice principal de v en el árbol de rutas más cortas. El padre de la raíz (o vértice de origen) es -1. Cada vez que encontramos un camino más corto a través de un vértice u, hacemos que u sea el padre del vértice actual.
Una vez que hemos construido la array principal, podemos imprimir la ruta usando la siguiente función recursiva.
void printPath(int parent[], int j)
{
// Base Case : If j is source
if (parent[j]==-1)
return;
printPath(parent, parent[j]);
printf("%d ", j);
}
A continuación se muestra la implementación completa.
C++
// C++ program for Dijkstra's single source shortest path
// algorithm.The program is for adjacency matrix
// representation of the graph.
#include <bits/stdc++.h>
using namespace std;
// Number of vertices in the graph
#define V 9
// A utility function to find the vertex with minimum
// distance value, from the set of vertices not yet included
// in shortest path tree
int minDistance(int dist[], bool sptSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int i = 0; i < V; i++)
if (sptSet[i] == false && dist[i] <= min)
min = dist[i], min_index = i;
return min_index;
}
// Function to print shortest path from source to j using
// parent array
void printPath(int parent[], int j)
{
// Base Case : If j is source
if (parent[j] == -1)
return;
printPath(parent, parent[j]);
cout << j << " ";
}
// A utility function to print the constructed distance
// array
int printSolution(int dist[], int n, int parent[])
{
int src = 0;
cout << "Vertex\t Distance\tPath";
for (int i = 1; i < V; i++) {
printf("\n%d -> %d \t\t %d\t\t%d ", src, i, dist[i],
src);
printPath(parent, i);
}
}
// Function that implements Dijkstra's single source
// shortest path algorithm for a graph represented using
// adjacency matrix representation
void dijkstra(int graph[V][V], int src)
{
// The output array. dist[i] will hold the shortest
// distance from src to i
int dist[V];
// sptSet[i] will true if vertex i is included / in
// shortest path tree or shortest distance from src to i
// is finalized
bool sptSet[V] = { false };
// Parent array to store shortest path tree
int parent[V] = { -1 };
// Initialize all distances as INFINITE
for (int i = 0; i < V; i++)
dist[i] = INT_MAX;
// Distance of source vertex from itself is always 0
dist[src] = 0;
// Find shortest path for all vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum distance vertex from the set of
// vertices not yet processed. u is always equal to
// src in first iteration.
int u = minDistance(dist, sptSet);
// Mark the picked vertex as processed
sptSet[u] = true;
// Update dist value of the adjacent vertices of the
// picked vertex.
for (int v = 0; v < V; v++)
// Update dist[v] only if is not in sptSet,
// there is an edge from u to v, and total
// weight of path from src to v through u is
// smaller than current value of dist[v]
if (!sptSet[v] && graph[u][v]
&& dist[u] + graph[u][v] < dist[v]) {
parent[v] = u;
dist[v] = dist[u] + graph[u][v];
}
}
// print the constructed distance array
printSolution(dist, V, parent);
}
// Driver Code
int main()
{
// Let us create the example graph discussed above
int graph[V][V] = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 0, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 14, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
dijkstra(graph, 0);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
C
// C program for Dijkstra's single source shortest path
// algorithm.The program is for adjacency matrix
// representation of the graph.
#include <limits.h> // To use the INT_MAX
#include <stdbool.h>
#include <stdio.h>
// Number of vertices in the graph
#define V 9
// A utility function to find the vertex with minimum
// distance value, from the set of vertices not yet included
// in shortest path tree
int minDistance(int dist[], bool sptSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (sptSet[v] == false && dist[v] <= min)
min = dist[v], min_index = v;
return min_index;
}
// Function to print shortest path from source to j using
// parent array
void printPath(int parent[], int j)
{
// Base Case : If j is source
if (parent[j] == -1)
return;
printPath(parent, parent[j]);
printf("%d ", j);
}
// A utility function to print the constructed distance
// array
int printSolution(int dist[], int n, int parent[])
{
int src = 0;
printf("Vertex\t Distance\tPath");
for (int i = 1; i < V; i++) {
printf("\n%d -> %d \t\t %d\t\t%d ", src, i, dist[i], src);
printPath(parent, i);
}
}
// Function that implements Dijkstra's single source
// shortest path algorithm for a graph represented using
// adjacency matrix representation
void dijkstra(int graph[V][V], int src)
{
// The output array. dist[i] will hold the shortest
// distance from src to i
int dist[V];
// sptSet[i] will true if vertex i is included / in
// shortest path tree or shortest distance from src to i
// is finalized
bool sptSet[V] = { false };
// Parent array to store shortest path tree
int parent[V] = { -1 };
// Initialize all distances as INFINITE and stpSet[] as
// false
for (int i = 0; i < V; i++) {
dist[i] = INT_MAX;
}
// Distance of source vertex from itself is always 0
dist[src] = 0;
// Find shortest path for all vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum distance vertex from the set of
// vertices not yet processed. u is always equal to
// src in first iteration.
int u = minDistance(dist, sptSet);
// Mark the picked vertex as processed
sptSet[u] = true;
// Update dist value of the adjacent vertices of the
// picked vertex.
for (int v = 0; v < V; v++)
// Update dist[v] only if is not in sptSet,
// there is an edge from u to v, and total
// weight of path from src to v through u is
// smaller than current value of dist[v]
if (!sptSet[v] && graph[u][v]
&& dist[u] + graph[u][v] < dist[v]) {
parent[v] = u;
dist[v] = dist[u] + graph[u][v];
}
}
// print the constructed distance array
printSolution(dist, V, parent);
}
// Driver Code
int main()
{
// Let us create the example graph discussed above
int graph[V][V] = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 0, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 14, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
dijkstra(graph, 0);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
Java
// A Java program for Dijkstra's
// single source shortest path
// algorithm. The program is for
// adjacency matrix representation
// of the graph.
class DijkstrasAlgorithm {
private static final int NO_PARENT = -1;
// Function that implements Dijkstra's
// single source shortest path
// algorithm for a graph represented
// using adjacency matrix
// representation
private static void dijkstra(int[][] adjacencyMatrix,
int startVertex)
{
int nVertices = adjacencyMatrix[0].length;
// shortestDistances[i] will hold the
// shortest distance from src to i
int[] shortestDistances = new int[nVertices];
// added[i] will true if vertex i is
// included / in shortest path tree
// or shortest distance from src to
// i is finalized
boolean[] added = new boolean[nVertices];
// Initialize all distances as
// INFINITE and added[] as false
for (int vertexIndex = 0; vertexIndex < nVertices;
vertexIndex++)
{
shortestDistances[vertexIndex] = Integer.MAX_VALUE;
added[vertexIndex] = false;
}
// Distance of source vertex from
// itself is always 0
shortestDistances[startVertex] = 0;
// Parent array to store shortest
// path tree
int[] parents = new int[nVertices];
// The starting vertex does not
// have a parent
parents[startVertex] = NO_PARENT;
// Find shortest path for all
// vertices
for (int i = 1; i < nVertices; i++)
{
// Pick the minimum distance vertex
// from the set of vertices not yet
// processed. nearestVertex is
// always equal to startNode in
// first iteration.
int nearestVertex = -1;
int shortestDistance = Integer.MAX_VALUE;
for (int vertexIndex = 0;
vertexIndex < nVertices;
vertexIndex++)
{
if (!added[vertexIndex] &&
shortestDistances[vertexIndex] <
shortestDistance)
{
nearestVertex = vertexIndex;
shortestDistance = shortestDistances[vertexIndex];
}
}
// Mark the picked vertex as
// processed
added[nearestVertex] = true;
// Update dist value of the
// adjacent vertices of the
// picked vertex.
for (int vertexIndex = 0;
vertexIndex < nVertices;
vertexIndex++)
{
int edgeDistance = adjacencyMatrix[nearestVertex][vertexIndex];
if (edgeDistance > 0
&& ((shortestDistance + edgeDistance) <
shortestDistances[vertexIndex]))
{
parents[vertexIndex] = nearestVertex;
shortestDistances[vertexIndex] = shortestDistance +
edgeDistance;
}
}
}
printSolution(startVertex, shortestDistances, parents);
}
// A utility function to print
// the constructed distances
// array and shortest paths
private static void printSolution(int startVertex,
int[] distances,
int[] parents)
{
int nVertices = distances.length;
System.out.print("Vertex\t Distance\tPath");
for (int vertexIndex = 0;
vertexIndex < nVertices;
vertexIndex++)
{
if (vertexIndex != startVertex)
{
System.out.print("\n" + startVertex + " -> ");
System.out.print(vertexIndex + " \t\t ");
System.out.print(distances[vertexIndex] + "\t\t");
printPath(vertexIndex, parents);
}
}
}
// Function to print shortest path
// from source to currentVertex
// using parents array
private static void printPath(int currentVertex,
int[] parents)
{
// Base case : Source node has
// been processed
if (currentVertex == NO_PARENT)
{
return;
}
printPath(parents[currentVertex], parents);
System.out.print(currentVertex + " ");
}
// Driver Code
public static void main(String[] args)
{
int[][] adjacencyMatrix = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 0, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 14, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
dijkstra(adjacencyMatrix, 0);
}
}
// This code is contributed by Harikrishnan Rajan
Python3
# Python program for Dijkstra's
# single source shortest
# path algorithm. The program
# is for adjacency matrix
# representation of the graph
from collections import defaultdict
#Class to represent a graph
class Graph:
# A utility function to find the
# vertex with minimum dist value, from
# the set of vertices still in queue
def minDistance(self,dist,queue):
# Initialize min value and min_index as -1
minimum = float("Inf")
min_index = -1
# from the dist array,pick one which
# has min value and is till in queue
for i in range(len(dist)):
if dist[i] < minimum and i in queue:
minimum = dist[i]
min_index = i
return min_index
# Function to print shortest path
# from source to j
# using parent array
def printPath(self, parent, j):
#Base Case : If j is source
if parent[j] == -1 :
print(j,end=" ")
return
self.printPath(parent , parent[j])
print (j,end=" ")
# A utility function to print
# the constructed distance
# array
def printSolution(self, dist, parent):
src = 0
print("Vertex \t\tDistance from Source\tPath")
for i in range(1, len(dist)):
print("\n%d --> %d \t\t%d \t\t\t\t\t" % (src, i, dist[i]),end=" ")
self.printPath(parent,i)
'''Function that implements Dijkstra's single source shortest path
algorithm for a graph represented using adjacency matrix
representation'''
def dijkstra(self, graph, src):
row = len(graph)
col = len(graph[0])
# The output array. dist[i] will hold
# the shortest distance from src to i
# Initialize all distances as INFINITE
dist = [float("Inf")] * row
#Parent array to store
# shortest path tree
parent = [-1] * row
# Distance of source vertex
# from itself is always 0
dist[src] = 0
# Add all vertices in queue
queue = []
for i in range(row):
queue.append(i)
#Find shortest path for all vertices
while queue:
# Pick the minimum dist vertex
# from the set of vertices
# still in queue
u = self.minDistance(dist,queue)
# remove min element
queue.remove(u)
# Update dist value and parent
# index of the adjacent vertices of
# the picked vertex. Consider only
# those vertices which are still in
# queue
for i in range(col):
'''Update dist[i] only if it is in queue, there is
an edge from u to i, and total weight of path from
src to i through u is smaller than current value of
dist[i]'''
if graph[u][i] and i in queue:
if dist[u] + graph[u][i] < dist[i]:
dist[i] = dist[u] + graph[u][i]
parent[i] = u
# print the constructed distance array
self.printSolution(dist,parent)
g= Graph()
graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],
[4, 0, 8, 0, 0, 0, 0, 11, 0],
[0, 8, 0, 7, 0, 4, 0, 0, 2],
[0, 0, 7, 0, 9, 14, 0, 0, 0],
[0, 0, 0, 9, 0, 10, 0, 0, 0],
[0, 0, 4, 14, 10, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 1, 6],
[8, 11, 0, 0, 0, 0, 1, 0, 7],
[0, 0, 2, 0, 0, 0, 6, 7, 0]
]
# Print the solution
g.dijkstra(graph,0)
# This code is contributed by Neelam Yadav
C#
// C# program for Dijkstra's
// single source shortest path
// algorithm. The program is for
// adjacency matrix representation
// of the graph.
using System;
public class DijkstrasAlgorithm
{
private static readonly int NO_PARENT = -1;
// Function that implements Dijkstra's
// single source shortest path
// algorithm for a graph represented
// using adjacency matrix
// representation
private static void dijkstra(int[,] adjacencyMatrix,
int startVertex)
{
int nVertices = adjacencyMatrix.GetLength(0);
// shortestDistances[i] will hold the
// shortest distance from src to i
int[] shortestDistances = new int[nVertices];
// added[i] will true if vertex i is
// included / in shortest path tree
// or shortest distance from src to
// i is finalized
bool[] added = new bool[nVertices];
// Initialize all distances as
// INFINITE and added[] as false
for (int vertexIndex = 0; vertexIndex < nVertices;
vertexIndex++)
{
shortestDistances[vertexIndex] = int.MaxValue;
added[vertexIndex] = false;
}
// Distance of source vertex from
// itself is always 0
shortestDistances[startVertex] = 0;
// Parent array to store shortest
// path tree
int[] parents = new int[nVertices];
// The starting vertex does not
// have a parent
parents[startVertex] = NO_PARENT;
// Find shortest path for all
// vertices
for (int i = 1; i < nVertices; i++)
{
// Pick the minimum distance vertex
// from the set of vertices not yet
// processed. nearestVertex is
// always equal to startNode in
// first iteration.
int nearestVertex = -1;
int shortestDistance = int.MaxValue;
for (int vertexIndex = 0;
vertexIndex < nVertices;
vertexIndex++)
{
if (!added[vertexIndex] &&
shortestDistances[vertexIndex] <
shortestDistance)
{
nearestVertex = vertexIndex;
shortestDistance = shortestDistances[vertexIndex];
}
}
// Mark the picked vertex as
// processed
added[nearestVertex] = true;
// Update dist value of the
// adjacent vertices of the
// picked vertex.
for (int vertexIndex = 0;
vertexIndex < nVertices;
vertexIndex++)
{
int edgeDistance = adjacencyMatrix[nearestVertex,vertexIndex];
if (edgeDistance > 0
&& ((shortestDistance + edgeDistance) <
shortestDistances[vertexIndex]))
{
parents[vertexIndex] = nearestVertex;
shortestDistances[vertexIndex] = shortestDistance +
edgeDistance;
}
}
}
printSolution(startVertex, shortestDistances, parents);
}
// A utility function to print
// the constructed distances
// array and shortest paths
private static void printSolution(int startVertex,
int[] distances,
int[] parents)
{
int nVertices = distances.Length;
Console.Write("Vertex\t Distance\tPath");
for (int vertexIndex = 0;
vertexIndex < nVertices;
vertexIndex++)
{
if (vertexIndex != startVertex)
{
Console.Write("\n" + startVertex + " -> ");
Console.Write(vertexIndex + " \t\t ");
Console.Write(distances[vertexIndex] + "\t\t");
printPath(vertexIndex, parents);
}
}
}
// Function to print shortest path
// from source to currentVertex
// using parents array
private static void printPath(int currentVertex,
int[] parents)
{
// Base case : Source node has
// been processed
if (currentVertex == NO_PARENT)
{
return;
}
printPath(parents[currentVertex], parents);
Console.Write(currentVertex + " ");
}
// Driver Code
public static void Main(String[] args)
{
int[,] adjacencyMatrix = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 0, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 14, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
dijkstra(adjacencyMatrix, 0);
}
}
// This code has been contributed by 29AjayKumar
Javascript
<script>
// A Javascript program for Dijkstra's
// single source shortest path
// algorithm. The program is for
// adjacency matrix representation
// of the graph.
let NO_PARENT = -1;
function dijkstra(adjacencyMatrix,startVertex)
{
let nVertices = adjacencyMatrix[0].length;
// shortestDistances[i] will hold the
// shortest distance from src to i
let shortestDistances = new Array(nVertices);
// added[i] will true if vertex i is
// included / in shortest path tree
// or shortest distance from src to
// i is finalized
let added = new Array(nVertices);
// Initialize all distances as
// INFINITE and added[] as false
for (let vertexIndex = 0; vertexIndex < nVertices;
vertexIndex++)
{
shortestDistances[vertexIndex] = Number.MAX_VALUE;
added[vertexIndex] = false;
}
// Distance of source vertex from
// itself is always 0
shortestDistances[startVertex] = 0;
// Parent array to store shortest
// path tree
let parents = new Array(nVertices);
// The starting vertex does not
// have a parent
parents[startVertex] = NO_PARENT;
// Find shortest path for all
// vertices
for (let i = 1; i < nVertices; i++)
{
// Pick the minimum distance vertex
// from the set of vertices not yet
// processed. nearestVertex is
// always equal to startNode in
// first iteration.
let nearestVertex = -1;
let shortestDistance = Number.MAX_VALUE;
for (let vertexIndex = 0;
vertexIndex < nVertices;
vertexIndex++)
{
if (!added[vertexIndex] &&
shortestDistances[vertexIndex] <
shortestDistance)
{
nearestVertex = vertexIndex;
shortestDistance = shortestDistances[vertexIndex];
}
}
// Mark the picked vertex as
// processed
added[nearestVertex] = true;
// Update dist value of the
// adjacent vertices of the
// picked vertex.
for (let vertexIndex = 0;
vertexIndex < nVertices;
vertexIndex++)
{
let edgeDistance = adjacencyMatrix[nearestVertex][vertexIndex];
if (edgeDistance > 0
&& ((shortestDistance + edgeDistance) <
shortestDistances[vertexIndex]))
{
parents[vertexIndex] = nearestVertex;
shortestDistances[vertexIndex] = shortestDistance +
edgeDistance;
}
}
}
printSolution(startVertex, shortestDistances, parents);
}
function printSolution(startVertex,distances,parents)
{
let nVertices = distances.length;
document.write("Vertex Distance Path");
for (let vertexIndex = 0;
vertexIndex < nVertices;
vertexIndex++)
{
if (vertexIndex != startVertex)
{
document.write("<br>" + startVertex + " -> ");
document.write(vertexIndex + " ");
document.write(distances[vertexIndex] + " ");
printPath(vertexIndex, parents);
}
}
}
function printPath(currentVertex,parents)
{
// Base case : Source node has
// been processed
if (currentVertex == NO_PARENT)
{
return;
}
printPath(parents[currentVertex], parents);
document.write(currentVertex + " ");
}
let graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],
[4, 0, 8, 0, 0, 0, 0, 11, 0],
[0, 8, 0, 7, 0, 4, 0, 0, 2],
[0, 0, 7, 0, 9, 14, 0, 0, 0],
[0, 0, 0, 9, 0, 10, 0, 0, 0],
[0, 0, 4, 14, 10, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 1, 6],
[8, 11, 0, 0, 0, 0, 1, 0, 7],
[0, 0, 2, 0, 0, 0, 6, 7, 0]
];
dijkstra(graph,0)
// This code is contributed by rag2127.
</script>
Vertex Distance Path 0 -> 1 4 0 1 0 -> 2 12 0 1 2 0 -> 3 19 0 1 2 3 0 -> 4 21 0 7 6 5 4 0 -> 5 11 0 7 6 5 0 -> 6 9 0 7 6 0 -> 7 8 0 7 0 -> 8 14 0 1 2 8
Este artículo es una contribución de Aditya Goel . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA