Incrementos o decrementos mínimos necesarios para convertir una array ordenada en una secuencia de potencia

Dada una array ordenada arr[] que consta de N enteros positivos, la tarea es minimizar el número total de incrementos o decrementos de cada elemento de la array necesarios para convertir la array dada en una secuencia de potencias de cualquier entero arbitrario X .

Una secuencia se llama secuencia de potencia de cualquier entero X , si y solo si para cada i ^ésimo elemento (0 ≤ i < N), arr[i] = X ⁱ , donde N es la longitud de la array dada.

Ejemplos:

Entrada: arr[] = {1, 3, 4}
Salida: 1
Explicación: La disminución de arr[1] en 1 modifica la array a {1, 2, 4}, que es una secuencia de potencias de 2. Por lo tanto, el número total de incrementos o decrementos requeridos es 1.

Entrada: arr[] = {1, 5, 7}
Salida: 6
Explicación:
Operación 1: Disminuir arr[1] en 1 modifica el arreglo a {1, 4, 7}
Operación 2: Disminuir arr[1] en 1 modifica el arreglo a {1, 3, 7}
Operación 3: aumentar arr[2] en 1 modifica el arreglo a {1, 3, 8}
Operación 4: aumentar arr[2] en 1 modifica el arreglo a {1, 3, 9}, lo cual es la secuencia de potencia de 3. Por lo tanto, el número total de incrementos o decrementos requeridos es 4.

Enfoque: El problema dado se puede resolver con base en las siguientes observaciones:

Como la array dada debe convertirse en una secuencia de potencias para cualquier número entero arbitrario X , las relaciones matemáticas se pueden escribir como:

$f(X) = \sum{\lvert a_i - X^i \rvert}$
donde, 0 <= i < N, N es el número de elementos en la array.

El valor mínimo de f(X) es el número mínimo de operaciones requeridas para convertirlo en una secuencia de potencia de X y el valor máximo de X se puede calcular de la siguiente manera:

=> $X^{N - 1} - a[N - 1] \le f(c) \le f(1)$
=> $X^{N - 1} \le f(1) + a{[N - 1]}$

Por lo tanto, la idea es iterar para todos los valores posibles de X a partir de 1 , y comprobar si la siguiente ecuación se cumple o no:
$X^{N - 1} \le f(1) + a{[N - 1]}$
Si se encuentra que es verdadera, entonces encuentre todos los valores posibles de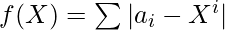 $f(X) = \sum{\lvert a_i - X^i \rvert}$ y devuelva el mínimo entre todos los valores obtenidos.

Siga los pasos a continuación para resolver el problema dado:

Inicialice una variable, digamos ans as ( la suma de los elementos del arreglo – N) , que almacene el número mínimo de incrementos o decrementos requeridos para hacer del arreglo una secuencia de potencia.
Itere un ciclo, comenzando desde 1 , usando la variable X y realice los siguientes pasos:
- Inicialice dos variables, digamos currCost como 0 y currPower como 1 , que almacena la suma de la expresión 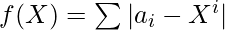$f(X) = \sum{\lvert a_i - X^i \rvert}$ y la potencia del entero X .
- Itere sobre el rango [0, N – 1] y actualice el valor de currCost como currCost + abs(arr[i] – currPower) y el valor de currPower como X * currPower .
- Si la expresión $X^{N - 1} \le ans + a{[N - 1]}$ no se cumple, salga del bucle . De lo contrario, actualice el valor de ans al mínimo de ans y currCost .
Después de completar los pasos anteriores, imprima el valor de ans como el número mínimo requerido de operaciones.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the minimum number
// of increments or decrements required
// to convert array into a power sequence
int minOperations(int a[], int n)
{
    // Initialize the count to f(X) for X = 1
    int ans = accumulate(a, a + n, 0) - n;
 
    // Calculate the value of f(X)
    // X ^ (n - 1) <= f(1) + a[n - 1]
    for (int x = 1;; x++) {
 
        int curPow = 1, curCost = 0;
 
        // Calculate F(x)
        for (int i = 0; i < n; i++) {
            curCost += abs(a[i] - curPow);
            curPow *= x;
        }
 
        // Check if X ^ (n - 1) > f(1) + a[n - 1]
        if (curPow / x > ans + a[n - 1])
            break;
 
        // Update ans to store the
        // minimum of ans and F(x)
        ans = min(ans, curCost);
    }
 
    // Return the minimum number
    // of operations required
    return ans;
}
 
// Driver Code
int main()
{
    int arr[] = { 1, 5, 7 };
    int N = sizeof(arr) / sizeof(arr[0]);
 
    cout << minOperations(arr, N);
 
    return 0;
}

Java

// Java program for the above approach
class GFG{
 
// Function to find the minimum number
// of increments or decrements required
// to convert array into a power sequence
static int minOperations(int a[], int n)
{
     
    // Initialize the count to f(X) for X = 1
    int ans = 0;
    for(int i = 0; i < n; i++)
    {
        ans += a[i];
    }
    ans -= n;
 
    // Calculate the value of f(X)
    // X ^ (n - 1) <= f(1) + a[n - 1]
    for(int x = 1;; x++)
    {
        int curPow = 1, curCost = 0;
 
        // Calculate F(x)
        for(int i = 0; i < n; i++)
        {
            curCost += Math.abs(a[i] - curPow);
            curPow *= x;
        }
 
        // Check if X ^ (n - 1) > f(1) + a[n - 1]
        if (curPow / x > ans + a[n - 1])
            break;
 
        // Update ans to store the
        // minimum of ans and F(x)
        ans = Math.min(ans, curCost);
    }
 
    // Return the minimum number
    // of operations required
    return ans;
}
 
// Driver Code
public static void main(String[] args)
{
    int arr[] = { 1, 5, 7 };
    int N = arr.length;
 
    System.out.print(minOperations(arr, N));
}
}
 
// This code is contributed by avijitmondal1998

Python3

# Python3 program for the above approach
 
# Function to find the minimum number
# of increments or decrements required
# to convert array into a power sequence
def minOperations(a, n):
     
    # Initialize the count to f(X) for X = 1
    ans = 0
    for i in range(n):
        ans += a[i]
         
    ans -= n
 
    # Calculate the value of f(X)
    # X ^ (n - 1) <= f(1) + a[n - 1]
    x = 1
    while(1):
        curPow = 1
        curCost = 0
 
        # Calculate F(x)
        for i in range(n):
            curCost += abs(a[i] - curPow)
            curPow *= x
 
        # Check if X ^ (n - 1) > f(1) + a[n - 1]
        if (curPow / x > ans + a[n - 1]):
            break
 
        # Update ans to store the
        # minimum of ans and F(x)
        ans = min(ans, curCost)
        x += 1
 
    # Return the minimum number
    # of operations required
    return ans
 
# Driver Code
if __name__ == '__main__':
     
    arr =  [1, 5, 7]
    N = len(arr)
     
    print(minOperations(arr, N))
     
# This code is contributed by ipg2016107

C#

// C# program for the above approach
using System;
 
class GFG{
 
// Function to find the minimum number
// of increments or decrements required
// to convert array into a power sequence
static int minOperations(int []a, int n)
{
     
    // Initialize the count to f(X) for X = 1
    int ans = 0;
    for(int i = 0; i < n; i++)
    {
        ans += a[i];
    }
    ans -= n;
 
    // Calculate the value of f(X)
    // X ^ (n - 1) <= f(1) + a[n - 1]
    for(int x = 1;; x++)
    {
        int curPow = 1, curCost = 0;
 
        // Calculate F(x)
        for(int i = 0; i < n; i++)
        {
            curCost += Math.Abs(a[i] - curPow);
            curPow *= x;
        }
 
        // Check if X ^ (n - 1) > f(1) + a[n - 1]
        if (curPow / x > ans + a[n - 1])
            break;
 
        // Update ans to store the
        // minimum of ans and F(x)
        ans = Math.Min(ans, curCost);
    }
 
    // Return the minimum number
    // of operations required
    return ans;
}
 
// Driver Code
public static void Main()
{
    int []arr = { 1, 5, 7 };
    int N = arr.Length;
 
    Console.WriteLine(minOperations(arr, N));
}
}
 
// This code is contributed by mohit kumar 29

Javascript

<script>
 
// JavaScript program for the above approach   
 
// Function to find the minimum number
// of increments or decrements required
// to convert array into a power sequence
    function minOperations(a , n) {
 
        // Initialize the count to f(X) for X = 1
        var ans = 0;
        for (i = 0; i < n; i++) {
            ans += a[i];
        }
        ans -= n;
 
        // Calculate the value of f(X)
        // X ^ (n - 1) <= f(1) + a[n - 1]
        for (x = 1;; x++) {
            var curPow = 1, curCost = 0;
 
            // Calculate F(x)
            for (i = 0; i < n; i++) {
                curCost += Math.abs(a[i] - curPow);
                curPow *= x;
            }
 
            // Check if X ^ (n - 1) > f(1) + a[n - 1]
            if (curPow / x > ans + a[n - 1])
                break;
 
            // Update ans to store the
            // minimum of ans and F(x)
            ans = Math.min(ans, curCost);
        }
 
        // Return the minimum number
        // of operations required
        return ans;
    }
 
    // Driver Code
     
        var arr = [ 1, 5, 7 ];
        var N = arr.length;
 
        document.write(minOperations(arr, N));
 
// This code contributed by aashish1995
 
</script>

Producción:

Complejidad de tiempo: O(N*(S) ^{(1/(N – 1))} )
Espacio auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por rupesh_rao y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta