El modelo de siembra de errores de Mills propuso un método de siembra de errores para estimar el número de errores en un programa introduciendo errores sembrados en el programa. A partir de los datos de depuración, que consisten en errores inherentes y errores inducidos, podría estimarse el número desconocido de errores inherentes. Si es igualmente probable que se detecten tanto los errores inherentes como los errores inducidos, entonces la probabilidad de k errores inducidos en r errores eliminados sigue una distribución hipergeométrica que viene dada por
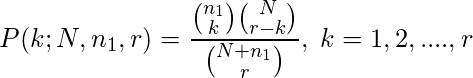
donde
N = número total de errores inherentes
n1 = número total de errores inducidos
r = número total de errores eliminados durante la depuración
k = número total de errores inducidos en r errores eliminados
r – k = número total de errores inherentes en r errores eliminados
Como se conocen n1, r y k, se puede demostrar que el MLE de N es
![]()
dónde
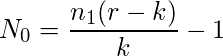
Si ![]() es un número entero, entonces
es un número entero, entonces ![]() y
y ![]() son los MLE de N.
son los MLE de N.
Inconvenientes:
- Es costoso realizar pruebas del software y, al mismo tiempo, aumenta el esfuerzo de prueba.
- Este método también fue criticado por su incapacidad para determinar el tipo, la ubicación y el nivel de dificultad de los errores inducidos de modo que se detectaran con la misma probabilidad que los errores inherentes.
Otro método realista para estimar los errores residuales en un programa se basa en dos grupos independientes de programadores que prueban el programa en busca de errores utilizando conjuntos independientes de casos de prueba. Supongamos que de un número total de N errores iniciales, el primer programador detecta n1 errores (y no los elimina en absoluto) y el segundo detecta de forma independiente r errores del mismo programa.
Suponga que ambos programadores encuentran k errores comunes. Si todos los errores tienen la misma posibilidad de ser detectados, entonces la fracción detectada por el primer programador (k) de un subconjunto de errores seleccionados al azar (p. ej., r) debe ser igual a la fracción que detecta el primer programador (n1) del número total de errores iniciales N. En otras palabras,
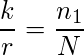
de modo que una estimación del número total de errores iniciales, N, es
![]()
La probabilidad de exactamente N errores iniciales con k errores comunes en r errores detectados por el segundo programador se puede obtener utilizando una distribución hipergeométrica de la siguiente manera:
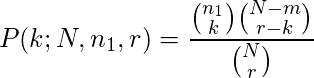
y el MLE de N es
![]()
que es lo mismo que el anterior.