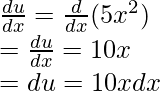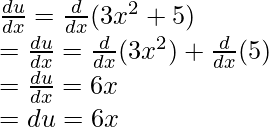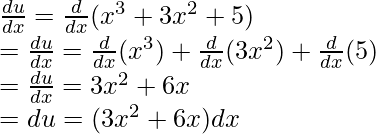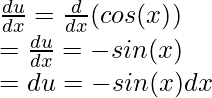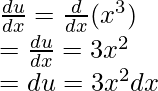Integración por sustitución de U

Encontrar integrales es básicamente un proceso de diferenciación inversa. Por eso a las integrales también se las llama antiderivadas. A menudo, las funciones son funciones sencillas y estándar que se pueden integrar fácilmente. Es más fácil resolver la combinación de estas funciones usando las propiedades de las integrales indefinidas. A veces las funciones se componen de composiciones de dos funciones, estos problemas son más difíciles de resolver utilizando la forma tradicional. En tales casos, entra en juego la regla de sustitución de U. Intuitivamente es justo lo contrario de la regla de la string. Veamos esta regla en detalle.

Integrales indefinidas

Considere una función derivada f'(x) definida y diferenciable en un intervalo. Las Integrales Indefinidas o antiderivadas nos permiten invertir el proceso de derivación y calcular la función F(x) cuya derivada nos es dada. Hay infinitas antiderivadas para cualquier derivada dada. Las integrales matemáticas se denotan con el símbolo ∫

F(x)= ∫ƒ(x) + C

Donde C es una constante arbitraria. La siguiente tabla muestra algunas convenciones y frases utilizadas en la integración con su significado.

Símbolo/Término/Significado	Sentido
∫f(x)dx	Integral de f con respecto a x
f(x) en ∫f(x)dx	integrando
x en ∫f(x)dx	Variable de integración
Integral de f(x)	Una función tal que F'(x) = f(x)

Es fundamental tener en cuenta las integrales de algunas funciones estándar para que la integración sea más sencilla y menos lenta. Las integrales de algunas funciones estándar se muestran a continuación.

Función	Integral
x ^norte	$\frac{x^{n+1}}{n +1}$
pecado(x)	-cos(x)
porque(x)	pecado(x)
e ^x	e ^x
segundo ² (x)	bronceado(x)
$\frac{1}{x}$	en(x)

Propiedades de las Integrales

Propiedad 1: ∫kf(x)dx= k∫f(x)dx

Propiedad 2: ∫f(x)± g(x)dx= ∫f(x)dx± ∫g(x)dx

Propiedad 3: ∫(f1(x)dx± f2(x)dx± f3(x)dx….)= ∫f1(x)dx± ∫f2(x)± ∫f3(x)dx…

Regla de sustitución U

La mayoría de las veces, las integrales se pueden calcular utilizando las propiedades y las fórmulas mencionadas anteriormente. Nos permiten calcular las integrales más simples en las que los integrandos suelen ser una combinación de algunas funciones simples y estándar. Por ejemplo, considere la función, f(x) = cos(x) + 5, la integral de esta función es fácil y se puede calcular fácilmente usando las propiedades mencionadas anteriormente. Pero ahora considere otra función, f(x) = sin(3x + 5). Esta función es una composición de dos funciones diferentes, la integral de esta función no es tan fácil como la anterior. Tales integrales se resuelven usando el método de sustitución de U.

∫f(g(x))g'(x)dx= ∫f(u)du

Aquí, u = g(x)

Considere un ejemplo para entender la regla.

f(x)= ∫2xcosx ² dx

Observe que la parte cos(x ² ) es una función compuesta. 2x es la derivada de la parte interna x ² . Entonces, digamos h(x) = x ² y w(x) = cos(x). Entonces, podemos asumir que u(x) = x ² y w(x) = cos(x),

$\overbrace{2x}^{u'}cos(\overbrace{x^2}^{u}) = u'(x)w(u(x))$

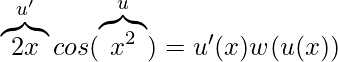
Esta es una formulación de sustitución. Considere u = x ²

$u' = 2x \\ \frac{du}{dx} = 2x \\ du = 2xdx$

Así, la función se convierte en,

f(x) = ∫cosu du

Esto se puede resolver usando fórmulas estándar,

f(x) = ∫cosu du = f(x) = seno + C = f(x) = senx ² + C

Veamos algunos problemas en esta regla,

Problemas de muestra

Pregunta 1: Encuentra la integral de la siguiente función f(x),

f(x)= ∫10x(5x ² )dx,

Solución:

Dado f(x)= ∫10x(5x ² )dx,

Sea F(x) la integral de la función f(x),

F(x)= ∫f(x)dx= F(x)= ∫10x(5x ² )dx

Observe que la función también es una función compuesta,

Sea u = 5x ² . Diferenciando la expresión,

$\frac{du}{dx} = \frac{d}{dx}(5x^2) \\ = \frac{du}{dx} = 10x \\ = du = 10xdx$

Usando estos resultados en la ecuación integral original,

F(x)= ∫f(x)dx= F(x)= ∫udu

$\\ = F(x) = \frac{u^2}{2} + C$

Sustituyendo el valor de “u” en la ecuación anterior,

F(x) = $\frac{(5x^2)^2}{2} + C$

Pregunta 2: Encuentra la integral de la siguiente función f(x),

f(x) = 6x(3x ² + 5)

Solución:

Dado f(x) = 6x(3x ² + 5),

Sea F(x) la integral de la función f(x),

F(x)= ∫f(x)dx= F(x)= ∫F(x)= ∫6x(3x ² + 5) dx

Observe que la función también es una función compuesta,

Sea u = 3x ² + 5. Derivando la expresión,

$\frac{du}{dx} = \frac{d}{dx}(3x^2 + 5 ) \\ = \frac{du}{dx} = \frac{d}{dx}(3x^2) + \frac{d}{dx}(5)\\ = \frac{du}{dx} = 6x \\ = du = 6x$

Usando estos resultados en la ecuación integral original,

F(x)= ∫f(x)dx= F(x)= udu

$\\ = F(x) = \frac{u^2}{2} + C$

Sustituyendo el valor de “u” en la ecuación anterior,

F(x) = $\frac{(3x^2 + 5)^2}{2} + C$

Pregunta 3: Encuentra la integral de la siguiente función f(x),

f(x)= ∫ (3x ² + 6x)(x ³ + 3×2+ 5)

Solución:

Dado f(x)= ∫ (3x ² + 6x)(x ³ + 3×2+ 5),

Sea F(x) la integral de la función f(x),

F(x)= ∫f(x)dx= F(x)= ∫ (3x ² + 6x)(x ³ + 3×2+ 5) dx

Observe que la función también es una función compuesta,

Sea u = x ³ + 3x ² + 5. Derivando la expresión,

$\frac{du}{dx} = \frac{d}{dx}(x^3 + 3x^2 + 5 ) \\ = \frac{du}{dx} = \frac{d}{dx}(x^3) + \frac{d}{dx}(3x^2) + \frac{d}{dx}(5)\\ = \frac{du}{dx} = 3x^2 + 6x \\ = du = (3x^2+6x)dx$

Usando estos resultados en la ecuación integral original,

F(x)= ∫f(x)dx= F(x)= ∫udu

$\\ = F(x) = \frac{u^2}{2} + C$

Sustituyendo el valor de “u” en la ecuación anterior,

F(x) = $\frac{(x^3 + 3x^2 + 5)^2}{2} + C$

Pregunta 4: Encuentra la integral de la siguiente función f(x),

f(x) = sen(x)cos(x)

Solución:

Dado f(x) = senxcosx,

Sea F(x) la integral de la función f(x),

F(x)= ∫f(x)dx= F(x)= ∫ senxcosxdx

Observe que la función también es una función compuesta,

Sea u = cos(x). Diferenciando la expresión,

$\frac{du}{dx} = \frac{d}{dx}(cos(x)) \\ = \frac{du}{dx} = -sin(x) \\ = du = -sin(x)dx$

Usando estos resultados en la ecuación integral original,

F(x)= ∫f(x)dx= F(x)= ∫ sen(x)cos(x)dx

F(x)= ∫-cos(x)(-sin(x))dx= F(x)= ∫-udu

$F(x) = \frac{-u^2}{2} + C$

Sustituyendo el valor de “u” en la ecuación anterior,

F(x) = $\frac{-u^2}{2} + C \\ = \frac{-(cos^2(x))}{2} + C$

Pregunta 5: Encuentra la integral de la siguiente función f(x),

f(x)= ∫ 3x ² cosx ³

Solución:

Dado f(x)= ∫ 3x ² cosx ³ ,

Sea F(x) la integral de la función f(x),

F(x)= ∫f(x)dx= F(x)= ∫ 3x ² cosx ³ dx

Observe que la función también es una función compuesta,

Sea u = x ^3. Derivando la expresión,

$\frac{du}{dx} = \frac{d}{dx}(x^3) \\ = \frac{du}{dx} = 3x^2 \\ = du = 3x^2dx$

Usando estos resultados en la ecuación integral original,

F(x)= ∫f(x)dx

F(x)= ∫3x2cos(x)dx

F(x)= ∫cosu du

F(x) = seno +C

Sustituyendo el valor de “u” en la ecuación anterior,

F(x) = sen(u) + C

⇒F(x) = sen(x ³ ) + C

Pregunta 6: Encuentra la integral de la siguiente función f(x),

f(x) = ∫3x ² cosx ³

Solución:

Dado f(x)= ∫3x ² cosx ³ ,

Sea F(x) la integral de la función f(x),

F(x)= ∫f(x)dx

F(x)= ∫3x ² cosx ³ dx

Observe que la función también es una función compuesta,

Sea u = x ^3. Derivando la expresión,

$\frac{du}{dx} = \frac{d}{dx}(x^3) \\ = \frac{du}{dx} = 3x^2 \\ = du = 3x^2dx$

Usando estos resultados en la ecuación integral original,

F(x)= ∫f(x)dx

F(x)= ∫3x ² cos(x)dx

F(x)= ∫cosu du

F(x)= sen(u)+ C

Sustituyendo el valor de “u” en la ecuación anterior,

F(x) = sen(u) + C

⇒F(x) = sen(x ³ ) + C

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Integrales indefinidas

Regla de sustitución U

Problemas de muestra

Deja una respuesta Cancelar la respuesta