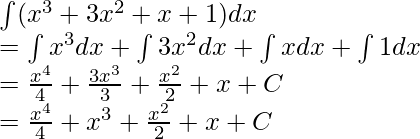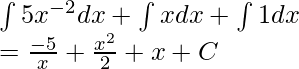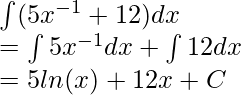El cálculo diferencial se centra en el concepto de derivada, las derivadas miden la tasa de cambio de los diferentes valores de la función. Geométricamente hablando, son la pendiente de la tangente en cualquier punto. Las integrales son el proceso inverso de diferenciación, las integrales están motivadas por la suma, así como las derivadas calculan la diferencia, las integrales calculan la suma para diferentes funciones, ahora bien, esta suma puede ser de cualquier cosa. Principalmente se utiliza para calcular el área y los volúmenes de formas arbitrarias. Veamos estos conceptos en detalle.
Introducción a las Integrales
Considere una función «f», que es derivable en el intervalo «I», lo que significa que su derivada existe en todos los puntos del intervalo I. Ahora, la pregunta que viene a la mente es, si la derivada de la función en cada punto se da, ¿es posible generar la función de nuevo? La función se llamará antiderivada. El proceso mediante el cual generamos estas funciones se llama integración y la fórmula que da estas antiderivadas se llama integral indefinida.
Integrales como el inverso de la diferenciación
Considere las derivadas de algunas funciones dadas a continuación,
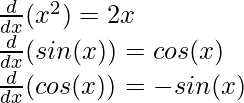
En las ecuaciones anteriores, considere ![]() , aquí x 2 es la antiderivada de la función f'(x) = 2x. Esto sigue también para los derivados anteriores.
, aquí x 2 es la antiderivada de la función f'(x) = 2x. Esto sigue también para los derivados anteriores.
Tenga en cuenta que si estas funciones se suman con constantes, no hay diferencia en las derivadas ya que la derivada de una constante es cero.

Entonces, se puede concluir que para cualquier función, sus antiderivadas son infinitas. Por ejemplo, para la función f(x), sea su antiderivada F(x),
![]()
![]() denotes the integration. This will represent the integration operation over any function. The table below represents the symbols and meanings related to integrals.
denotes the integration. This will represent the integration operation over any function. The table below represents the symbols and meanings related to integrals.
| Símbolo/Término/Significado | Sentido |
| Integral de f con respecto a x | |
| f(x) en |
integrando |
| x en |
Variable de integración |
| Integral de f(x) | Una función tal que F'(x) = f(x) |
Propiedades e integrales de algunas funciones estándar
Nos encontramos con muchas funciones todos los días, y se vuelve esencial aprender las propiedades de las integrales para simplificar el proceso de integración. También es necesario que se memoricen las integrales de algunas funciones estándar para que sea más fácil resolver las integrales complejas que suelen estar formadas por algunas funciones simples elementales. La siguiente tabla enumera algunas integrales de funciones estándar.
| Función | Integral |
| x norte | |
| pecado(x) | -cos(x) |
| porque(x) | pecado(x) |
| e x | e x |
| segundo 2 (x) | bronceado(x) |
| en(x) |
Propiedades de las integrales:
Propiedad 1:
Propiedad 2:
Propiedad 3:
Interpretación Geométrica de Integrales
Las integrales se utilizan generalmente para calcular las áreas bajo la curva. Aunque hay fórmulas disponibles, solo están disponibles para formas estándar. A menudo se encuentran formas arbitrariamente complejas y no es posible desarrollar y recordar una fórmula para cada forma. Así, las integrales ayudan a generalizar el método para calcular las áreas y el volumen. Considere una función f(x), el objetivo es calcular el área de la función.
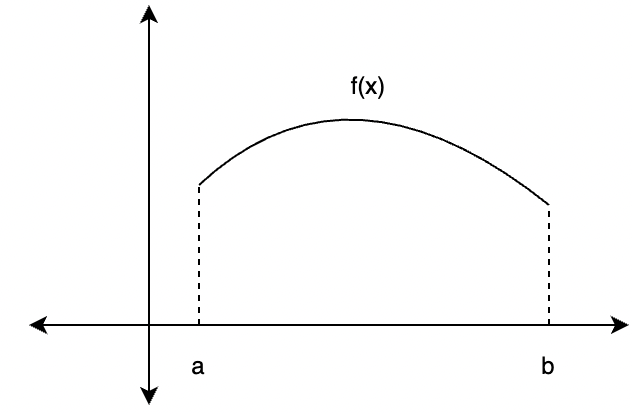
La función se divide en diferentes partes en forma de rectángulos, estas partes se suman y forman el área. El ancho de cada rectángulo es![]()
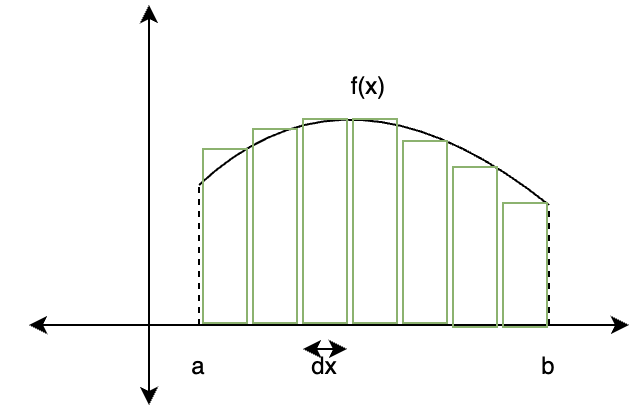
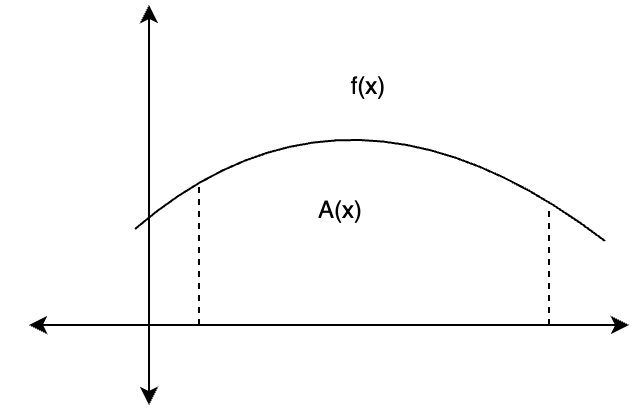
A medida que aumenta el número de rectángulos, el ancho de estos se vuelve muy pequeño y se puede indicar con «dx». El área de cada rectángulo se convierte en f(x)dx. El área total es la suma de las áreas de todos estos pequeños rectángulos,
![]()
Veamos algunos problemas de muestra.
Problemas de muestra
Pregunta 1: Encuentra la integral para la función dada f(x),
f(x) = 2sen(x) + 1
Solución:
Dado f(x) = 2sin(x) + 1
sin(x) es una función estándar y se conoce su integral.
⇒
Usando la propiedad 2 mencionada anteriormente,
⇒
Pregunta 2: Encuentra la integral para la función dada f(x),
f(x) = 2x 2 + 3x
Solución:
Dado f(x) =2x 2 + 3x
2x 2 + 3x es una función polinomial y se puede descomponer en diferentes partes.
⇒
Usando la propiedad 1 mencionada anteriormente,
Pregunta 3: Encuentra la integral para la función dada f(x),
f(x) = x3 + 3×2 + x + 1
Solución:
Dado f(x) = x 3 + 3x 2 + x + 1
x 3 + 3x 2 + x + 1 es una función polinomial y se puede descomponer en diferentes partes.
⇒
Usando la propiedad 1 mencionada anteriormente,
Pregunta 4: Encuentra la integral para la función dada f(x),
f(x) = 5x -2 + x + 1
Solución:
Dado f(x) = 5x -2 + x + 1
Usando la regla de la potencia inversa
⇒
Usando la propiedad 1 mencionada anteriormente,
Pregunta 5: Encuentra la integral para la función dada f(x),
f(x) = sen(x) + 5cos(x)
Solución:
Dado f(x) = sen(x) + 5cos(x)
sin(x) y cos(x) son funciones estándar y se conoce su integral.
⇒
Usando las propiedades 1 y 2 mencionadas anteriormente,
⇒
Pregunta 6: Encuentra la integral para la función dada f(x),
f(x) = 5x -2 + x4 + x
Solución:
Dado f(x) = 5x -2 + x 4 + x
Usando la regla de la potencia inversa
⇒
Usando las propiedades 1 y 2 y la regla de la potencia mencionada anteriormente,
⇒
⇒
Pregunta 7: Encuentra la integral para la función dada f(x),
f(x) = 5x -1 + 12
Solución:
Dado f(x) = 5x -1 + 12
Usando la regla de la potencia inversa
⇒
Usando las propiedades 1 y 2
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA