en los tipos
eje y hasta
La integración viene dada por ⇢
Ejemplo: Encuentre el área bajo el gráfico de la función y=4x, los límites se definen de 0 a 5 en el eje x. Resuelva tanto por integración como simplemente resolviendo el área usando la fórmula.
Solución:
La función en el gráfico se verá como,
El gráfico anterior muestra exactamente qué área se va a medir,
Integral de y=4x de 0 a 5 =
El área parece un triángulo y, por lo tanto, otra forma de resolver esto es simplemente hallar el área del triángulo.
Para la altura del triángulo, en x = 5, y = 4 × 5 = 20 unidades.
Base = 5 unidades, Altura = 20 unidades.
Área del triángulo = 1/2 × 5 × 20
= 10 × 5
= 50 unidades 2
Integrales definidas de funciones por partes
Para integrar funciones por partes, se requiere romper la integración en los puntos de ruptura exactos. Romper las integrales dará dos funciones diferentes para diferentes límites superior e inferior, y se vuelve fácil integrarlas por separado. Lo mismo se puede hacer para más de dos funciones, los puntos de ruptura y el número de integración aumentarán en tal caso.
Las funciones por partes se pueden representar como,
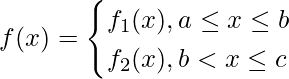
![]()
Aquí, el límite tiene un punto de quiebre en c, y las dos funciones son f 1 (x) y f 2 (x).
La función condicional anterior tiene integrales definidas de puntos finales fijos.
Función con puntos finales inferiores fijos, puntos finales superiores variables
Aplicación de Integrales definidas de función por partes
A continuación se muestran algunos ejemplos de funciones por partes que se ven muy a menudo en matemáticas,
- Función de módulo, |x|
La función de módulo son las funciones que se rompen en un punto, y se representan como,
- Función entera mayor, [x]
En integrales definidas, si el valor obtenido es algún decimal, la condición de entero mayor sacará la parte entera del valor, por ejemplo, [8.34] dará 8.
- Parte fraccionaria de la función, {x}
La parte fraccionaria de x se deriva u obtiene únicamente del entero mayor de la función.
Se define como, {x} = x-[x]
Problemas de muestra
Pregunta 1: Una función condicional se da como, 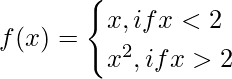
Encuentre la integral definida de ![]()
Solución:
La función condicional anterior tiene dos funciones involucradas, una es una línea recta y la otra es una parábola, el punto de quiebre del límite es 2 y debajo de 2, la función es una línea recta x, arriba de 2 o después de 2, es un parábola x 2 .
Teniendo esto en cuenta, la integral definida se puede descomponer fácilmente como,
Pregunta 2: Evalúa la integral definida ![]() , donde
, donde 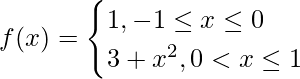
Solución :
La función anterior tiene dos funciones diferentes involucradas en diferentes límites, el punto de ruptura del límite es 0, y antes de -1, la función es 1, y después de 0 a 1, la función es 3+x 2 .
vamos a resolver,
Pregunta 3: Encuentra el área de la función dada a continuación con la ayuda de la integración definida,
Solución:
Hay tres funciones diferentes de -1 a 4, y=3, y=2+x, y=4. Integremos estas funciones con la ayuda de la integración de funciones por partes.
Pregunta 4: Resuelve la integración ![]() cuando la función se da como, f(x)= |x|.
cuando la función se da como, f(x)= |x|.
Solución:
La integración para módulo de x o |x| se puede resolver solo después de conocer el significado de |x|, |x| Se define como,
Por lo tanto, la función se puede descomponer como,
Pregunta 5: Evalúa la función dada, ![]()
Solución:
La función anterior es una función de módulo y, por lo tanto, tendrá un punto de ruptura, averigüemos el punto de ruptura para |2-x|,
Como se sabe que la función de módulo tendrá 2 valores, uno positivo y otro negativo, pero es importante averiguar dónde comienzan a cambiar los valores o la función en su conjunto,
El límite inferior es 0, si se pone 0, el valor que se obtiene es 2 que es positivo, ahora se pone 1, el valor que se obtiene es 1, pero si se pone cualquier valor por encima de 2, el valor es negativo, por lo tanto, el punto de quiebre es 2 .
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA


![Rendered by QuickLaTeX.com \int^5_0{4xdx}\\=4[\frac{x^2}{2}]^5_0\\=2[25-0]\\=50unit^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7cad883afe76e3466cd5c3be35ac3173_l3.png)
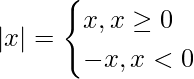
![Rendered by QuickLaTeX.com \int_0^4f(x)dx= \int_0^2xdx + \int_2^4x^2dx \\=[\frac{x^2}{2}]_0^2+[\frac{x^3}{3}]_2^4 \\=2+21.333-2.666\\=20.667](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-acd27c98c3967c2309fb3ca64f7e010d_l3.png)
![Rendered by QuickLaTeX.com \int_{-1}^1f(x)dx= \int_{-1}^01dx + \int_0^13+x^2dx\\=[x]_{-1}^0+[3x]_0^1+[\frac{x^3}{3}]_0^1\\=1+[3-0]+[1/3-0]\\=1+3+1/3\\=4+1/3\\=\frac{13}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-74635e65bf8472fbe71f40e647fef95b_l3.png)

![Rendered by QuickLaTeX.com \int_{-1}^4f(x)dx= \int_{-1}^13dx + \int_1^22+xdx + \int_2^44dx\\=[3x]_{-1}^1+[2x]_1^2+[\frac{x^2}{2}]_1^2+[4x]_2^4\\=6+3+2-0.5+16-8\\=19-0.5\\=18.5](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-82fc5fd9e568cfddf41ba0290f225d8d_l3.png)
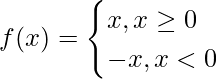
![Rendered by QuickLaTeX.com \int_{-1}^1f(x)dx= \int_{-1}^0-xdx+\int_{0}^1xdx\\=-[\frac{x^2}{2}]_{-1}^0+[\frac{x^2}{2}]_0^1\\=-[0-1/2]+[1/2]\\=1/2+1/2 \\=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c4392ac0171908f5dcd22cff7cad0d6d_l3.png)
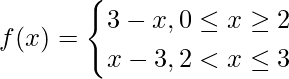
![Rendered by QuickLaTeX.com \int_0^3|3-x|dx= \int_0^2(3-x)dx+\int_2^3(x-3)dx\\=[3x]_0^2-[\frac{x^2}{2}]_0^2+[\frac{x^2}{2}]_2^3-[3x]_2^3\\=6-2+9/2-2+9-6\\=9.5](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-edc613ccafda5977364a57a6ad069361_l3.png)