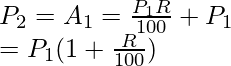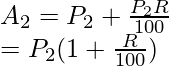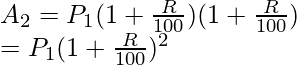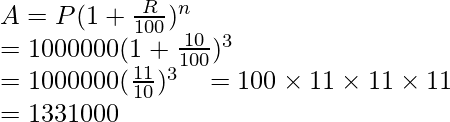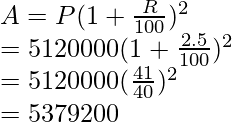Interés compuesto

La capitalización es un proceso de reinversión de las ganancias en su principal para obtener un rendimiento exponencial a medida que el próximo crecimiento se basa en un principal más grande, siguiendo este proceso de agregar ganancias al principal. En este paso del tiempo, el principal crecerá exponencialmente y producirá rendimientos inusuales.

A veces nos encontramos con declaraciones como «un año de interés para FD en el banco al 11 % anual». o “Cuenta de ahorro con interés @ 8% anual”. A la hora de invertir, suele haber dos tipos de intereses:

Interés simple
Interés compuesto

Ya conocemos el interés simple (SI), veremos el interés compuesto (CI) en detalle en este artículo. Primero, entendamos qué es lo que se compone a través de una historia.

Una vez, un prisionero estaba esperando su sentencia de muerte cuando el rey le pidió su último deseo.

El Prisionero exigió granos de arroz (una demanda tonta, ¿verdad?), pero agregó que la cantidad de granos debe duplicarse después de moverse a cada casilla hasta la última casilla del tablero de ajedrez (es decir, 1 en la primera, 2 en la segunda, 4 en la tercera, 8 en cuarto, 16 en quinto y así sucesivamente, hasta el cuadro 64).

El rey pensó que es una demanda muy pequeña y ordenó a sus ministros que calcularan esa cantidad de arroz y la proporcionaran al prisionero. La cantidad calculada fue tan grande que el rey perdió todo su reino y quedó en deuda con el prisionero toda su vida.

Lo que utilizó el preso fue la idea de “ Compounding ”. Ahora, definamos el interés compuesto.

El interés compuesto (o interés compuesto) es el interés de un préstamo o depósito calculado sobre la base tanto del capital inicial como del interés acumulado de períodos anteriores. Se cree que se originó en la Italia del siglo XVII, el interés compuesto se puede considerar como «interés sobre interés» y hará que una suma crezca a un ritmo más rápido que el interés simple, que se calcula solo sobre el monto principal.
Veamos un ejemplo antes de sacar la fórmula,

Pregunta: Hema tomó prestada una suma de Rs. 2,00,000 por 2 años a un interés del 8% compuesto anual de un banco. Encuentra el interés compuesto y la cantidad que tuvo que pagar al final de 2 años.

Respuesta :

Para hacerlo, necesitamos encontrar el interés año por año.

Paso 1. Primero encontremos el interés simple para el primer año,

Aquí, principal P ₁ = 2,00,000, R = 8% y T = 1.

SI ₁ = SI al 8% en P ₁ por un año = $\frac{P_{1} \times R \times T}{100} = \frac{200000 \times 8 \times 1}{100} = 16000$

Paso 2. Entonces, ahora la cantidad recibida al final del primer año = SI ₁ + P ₁ = 16000 + 2,00,000 = 2,16,000. Ahora, esto se convertirá en principal.

Así, P ₂ = 2,16 000, R = 8 y T = 1

Paso 3. Ahora encontraremos el interés simple para el segundo año tomando la cantidad total al final del primer año como principal P ₂ .

SI ₂ = SI al 8% en P ₂ por un año = $\frac{P_{2} \times R \times T}{100} = \frac{216000 \times 8 \times 1}{100} = 17280$

Esta cantidad ahora al final del segundo año = SI ₂ + P ₂ = 17280 + 2,16,000 = 2,33,280

Interés total dado = 17280 + 16000 = 33280.,

Debemos notar que el capital sigue siendo el mismo en el interés simple (SI), pero en el interés compuesto (CI) se recalcula y cambia cada año.

Fórmula para el interés compuesto

Derivemos la fórmula para el interés compuesto tomando solo el ejemplo anterior, pero esta vez no usaremos los valores para las variables.

$SI_{1} = \frac{P_{1} \times R}{100}$

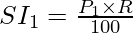
Ahora, la cantidad al final del primer año será el principal para el segundo año, es decir

$P_{2} = A_{1} = \frac{P_{1}R}{100} + P_{1} \\ \hspace{1.35cm} = P_{1}(1 + \frac{R}{100})$

Entonces, ahora SI para el segundo año

$SI_{2} = \frac{P_{2}R}{100}$

Cálculo de la cantidad para el segundo año,

$A_{2} = P_{2} + \frac{P_{2}R}{100} \\ \hspace{0.5cm} = P_{2}(1 + \frac{R}{100})$

Ahora usando el valor de P2 en la ecuación anterior,

$A_{2} = P_{1}(1 + \frac{R}{100})(1+\frac{R}{100})\\ \hspace{0.5cm} = P_{1}(1 + \frac{R}{100})^{2}$

Similar si seguimos calculando para “n” años,

Terminaremos con esta fórmula de cantidad

$A = P(1 + \frac{R}{100})^{n}$

donde P es el monto del capital inicial, R es la tasa y n es el número de años después de los cuales se calcula el monto.

Tasa compuesta anual o semestral

Puede notar que, al principio, usamos «tasa compuesta anual». ¿Qué significa?

Significa que el interés se capitalizó una vez al año. También podemos tener nuestro interés compuesto semestral o trimestralmente. ¿Qué sucede en tales casos?

Comparemos los dos casos a través de un ejemplo para ver la diferencia entre las tasas compuestas anualmente y semestralmente.

Supongamos que P = 1000, R = 5% y n = 2 años,

Caso 1: Interés compuesto anualmente.

$I = \frac{PR}{100} = \frac{1000 \times 5}{100} = 50$

A = 50 + 1000 = 1050.

Caso 2: Interés compuesto semestralmente.

$I = \frac{PRT}{100} = \frac{1000 \times 5 \times \frac{1}{2}}{100} = 25$

PAG ₂ = YO + PAG = 1025

$I_{2} = \frac{P_{2} RT }{100} = \frac{1025 \times 5 \times \frac{1}{2}}{100} = 25.625$

Importe final en este caso A = P ₂ + I ₂ = 1025 + 25,625 = 1050,625

Podemos que si el interés se capitaliza semestralmente, calcule el interés dos veces. Así que el período de tiempo se convierte en el doble y la tasa se toma la mitad.

Así que la fórmula se convierte en,

$A = P(1 + \frac{\frac{R}{2}}{100})^{2n}$

Aplicaciones de la fórmula de interés compuesto y ejemplos

Crecimiento y decadencia

El concepto de interés compuesto se puede aplicar a cualquier cantidad que aumente o disminuya de tal manera que la cantidad al final de cada período tenga una relación constante con la cantidad al comienzo de ese período.

Digamos que si la población de un pueblo aumenta de manera constante en un 2% anual de la población al comienzo de cada año, el factor de crecimiento anual es, es $(1+\frac{2}{100})$ decir, 1,02, y la población después de n años es (1,02) ⁿ veces la población al comienzo de cada año. ese periodo. Si la población disminuye en un 2%, entonces el factor de disminución anual es , por $(1−\frac{2}{100}),$ ejemplo, 0,98.

Pregunta: La población de un pueblo aumenta a razón de un 2,5% anual. Si su población actual es 3,26,40,000, encuentre la población después de 3 años.

Respuesta :

Podemos aplicar la fórmula de interés compuesto aquí,

La población “P” al cabo de 3 años será,

$P = 32640000(1+\frac{2.5}{100})^{3} \\ \hspace{0.38cm} = 32640000(1 + \frac{2.5}{100})^{3} \\ \hspace{0.38cm} = 32640000(1.025)^{3} \\ \hspace{0.38cm} = 35149710$

Apreciación y Depreciación

Cuando el valor de un artículo aumenta con el paso del tiempo, se dice que el artículo se aprecia. Cuando el valor de un artículo disminuye con el paso del tiempo, se dice que el artículo se deprecia.

Por ejemplo, si un hombre compra un automóvil y lo usa durante dos años, es obvio que el automóvil no valdrá la pena como uno nuevo. Por lo tanto, el automóvil se habrá depreciado en valor. Por otro lado, si un hombre compra un terreno, probablemente se dará cuenta de que en unos pocos años podrá obtener un mejor precio por él que el precio que pagó por él. El valor de la tierra se habrá apreciado así. Cuando las cosas son difíciles de obtener, tienen un valor de rareza y apreciación.

Pregunta: El valor de un piso residencial construido a un costo de Rs 10,00,000 se aprecia a una tasa del 10% anual. ¿Cuál será su valor 3 años después de la construcción?

Respuesta :

Valor del piso P = 1000000, tasa de apreciación = 10, n = 3

Después de 3 años, que el valor del piso sea «A».

$A = P(1 + \frac{R}{100})^{n} \\ \hspace{0.35cm} = 1000000( 1 + \frac{10}{100})^{3} \\ \hspace{0.35cm} = 1000000(\frac{11}{10})^{3} \hspace{0.35cm} = 100 \times 11 \times 11 \times 11 \\ \hspace{0.35cm} = 1331000$

Entonces, después de 3 años, el valor del piso será de 13,31,000.

El crecimiento de una bacteria si se conoce la tasa de crecimiento:

Pregunta: En cierto experimento, el recuento de bacterias aumentaba a razón de un 2,5 % por hora. Inicialmente, el conteo era 51,20,000. Encuentra la bacteria al cabo de 2 horas.

Responder:

Recuento inicial de bacterias = P = 51,20,000,

Tasa de aumento “r” = 2,5 por hora,

Queremos encontrar el conteo después de 2 horas, es decir; norte = 2

Que la cuenta final sea «A»

$A = P(1 + \frac{R}{100})^{2}\\ \hspace{0.36cm} = 5120000( 1 + \frac{2.5}{100})^{2} \\ \hspace{0.36cm} = 5120000( \frac{41}{40})^{2}\\ \hspace{0.36cm} = 5379200$

Entonces, el conteo final de bacterias es 53,79,200.

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA