Interpolación de Lagrange – Barcelona Geeks

¿Qué es la interpolación?
La interpolación es un método para encontrar nuevos puntos de datos dentro del rango de un conjunto discreto de puntos de datos conocidos (Fuente Wiki ). En otras palabras, la interpolación es la técnica para estimar el valor de una función matemática, para cualquier valor intermedio de la variable independiente.
Por ejemplo, en la tabla dada, tenemos 4 conjuntos de puntos de datos discretos, para una función desconocida f(x):

$\begin{array}{|c|c|c|c|c|} \hline \mathbf{i} & 1 & 2 & 3 & 4 \\ \hline \mathbf{x}_{\mathbf{i}} & 0 & 1 & 2 & 5 \\ \hline \mathbf{y}_{\mathbf{i}}=\mathbf{f}_{\mathbf{i}}(\mathbf{x}) & 2 & 3 & 12 & 147 \\ \hline \end{array}$

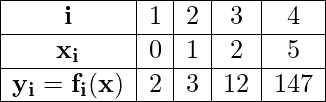
¿Como encontrar?
Aquí podemos aplicar la fórmula de interpolación de Lagrange para obtener nuestra solución.
La fórmula de la interpolación de Lagrange:
Si, y = f(x) toma los valores y0, y1, … , yn correspondientes a x = x0, x1 , … , xn entonces,

$f(x)=\frac{\left(x-x_{2}\right)\left(x-x_{3}\right) \ldots\left(x-x_{n}\right)}{\left(x_{1}-x_{2}\right)\left(x_{1}-x_{3}\right) \ldots\left(x_{1}-x_{n}\right)} y_{1}+\frac{\left(x-x_{1}\right)\left(x-x_{3}\right) \ldots\left(x-x_{n}\right)}{\left(x_{2}-x_{1}\right)\left(x_{2}-x_{3}\right) \ldots\left(x_{2}-x_{n}\right)} y_{2}+\ldots .+\frac{\left(x-x_{1}\right)\left(x-x_{2}\right) \ldots\left(x-x_{n}-1\right)}{\left(x_{n}-x_{1}\right)\left(x_{n}-x_{2}\right) \ldots\left(x_{n}-x_{n-1}\right)} y_{n}$
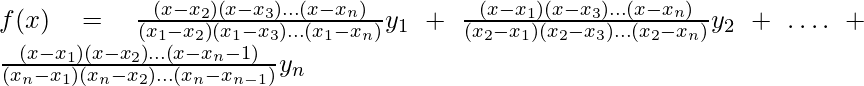
This method is preferred over its counterparts like Newton’s method because it is applicable even for unequally spaced values of x.
We can use interpolation techniques to find an intermediate data point say at x = 3.

Ventajas de la interpolación de Lagrange:

Esta fórmula se usa para encontrar el valor de la función incluso cuando los argumentos no están igualmente espaciados.
Esta fórmula se utiliza para encontrar el valor de la variable independiente x correspondiente a un valor dado de una función.

Desventajas de la interpolación de Lagrange:

Un cambio de grado en el polinomio lagrangiano implica un cálculo completamente nuevo de todos los términos.
Para un polinomio de alto grado, la fórmula implica una gran cantidad de multiplicaciones que hacen que el proceso sea bastante lento.
En la interpolación de Lagrange, el grado del polinomio se elige desde el principio. Por lo tanto, es difícil encontrar el grado de aproximación del polinomio que sea adecuado para un conjunto dado de puntos tabulados.

C++

// C++ program for implementation of Lagrange's Interpolation
#include<bits/stdc++.h>
using namespace std;
 
// To represent a data point corresponding to x and y = f(x)
struct Data
{
    int x, y;
};
 
// function to interpolate the given data points using Lagrange's formula
// xi corresponds to the new data point whose value is to be obtained
// n represents the number of known data points
double interpolate(Data f[], int xi, int n)
{
    double result = 0; // Initialize result
 
    for (int i=0; i<n; i++)
    {
        // Compute individual terms of above formula
        double term = f[i].y;
        for (int j=0;j<n;j++)
        {
            if (j!=i)
                term = term*(xi - f[j].x)/double(f[i].x - f[j].x);
        }
 
        // Add current term to result
        result += term;
    }
 
    return result;
}
 
// driver function to check the program
int main()
{
    // creating an array of 4 known data points
    Data f[] = {{0,2}, {1,3}, {2,12}, {5,147}};
 
    // Using the interpolate function to obtain a data point
    // corresponding to x=3
    cout << "Value of f(3) is : " << interpolate(f, 3, 5);
 
    return 0;
}

Java

// Java program for implementation
// of Lagrange's Interpolation
 
import java.util.*;
 
class GFG
{
 
// To represent a data point
// corresponding to x and y = f(x)
static class Data
{
    int x, y;
 
    public Data(int x, int y)
    {
        super();
        this.x = x;
        this.y = y;
    }
     
};
 
// function to interpolate the given
// data points using Lagrange's formula
// xi corresponds to the new data point
// whose value is to be obtained n
// represents the number of known data points
static double interpolate(Data f[], int xi, int n)
{
    double result = 0; // Initialize result
 
    for (int i = 0; i < n; i++)
    {
        // Compute individual terms of above formula
        double term = f[i].y;
        for (int j = 0; j < n; j++)
        {
            if (j != i)
                term = term*(xi - f[j].x) / (f[i].x - f[j].x);
        }
 
        // Add current term to result
        result += term;
    }
 
    return result;
}
 
// Driver code
public static void main(String[] args)
{
    // creating an array of 4 known data points
    Data f[] = {new Data(0, 2), new Data(1, 3),
                new Data(2, 12), new Data(5, 147)};
 
    // Using the interpolate function to obtain
    // a data point corresponding to x=3
    System.out.print("Value of f(3) is : " +
                    (int)interpolate(f, 3, 4));
}
}
 
// This code is contributed by 29AjayKumar

Python3

# Python3 program for implementation
# of Lagrange's Interpolation
 
# To represent a data point corresponding to x and y = f(x)
class Data:
    def __init__(self, x, y):
        self.x = x
        self.y = y
 
# function to interpolate the given data points
# using Lagrange's formula
# xi -> corresponds to the new data point
# whose value is to be obtained
# n -> represents the number of known data points
def interpolate(f: list, xi: int, n: int) -> float:
 
    # Initialize result
    result = 0.0
    for i in range(n):
 
        # Compute individual terms of above formula
        term = f[i].y
        for j in range(n):
            if j != i:
                term = term * (xi - f[j].x) / (f[i].x - f[j].x)
 
        # Add current term to result
        result += term
 
    return result
 
# Driver Code
if __name__ == "__main__":
 
    # creating an array of 4 known data points
    f = [Data(0, 2), Data(1, 3), Data(2, 12), Data(5, 147)]
 
    # Using the interpolate function to obtain a data point
    # corresponding to x=3
    print("Value of f(3) is :", interpolate(f, 3, 4))
 
# This code is contributed by
# sanjeev2552

C#

// C# program for implementation
// of Lagrange's Interpolation
using System;
 
class GFG
{
 
// To represent a data point
// corresponding to x and y = f(x)
class Data
{
    public int x, y;
    public Data(int x, int y)
    {
        this.x = x;
        this.y = y;
    }
};
 
// function to interpolate the given
// data points using Lagrange's formula
// xi corresponds to the new data point
// whose value is to be obtained n
// represents the number of known data points
static double interpolate(Data []f,
                          int xi, int n)
{
    double result = 0; // Initialize result
 
    for (int i = 0; i < n; i++)
    {
        // Compute individual terms
        // of above formula
        double term = f[i].y;
        for (int j = 0; j < n; j++)
        {
            if (j != i)
                term = term * (xi - f[j].x) /
                          (f[i].x - f[j].x);
        }
 
        // Add current term to result
        result += term;
    }
    return result;
}
 
// Driver code
public static void Main(String[] args)
{
    // creating an array of 4 known data points
    Data []f = {new Data(0, 2),
                new Data(1, 3),
                new Data(2, 12),
                new Data(5, 147)};
 
    // Using the interpolate function to obtain
    // a data point corresponding to x=3
    Console.Write("Value of f(3) is : " +
                  (int)interpolate(f, 3, 4));
}
}
 
// This code is contributed by PrinciRaj1992

Javascript

<script>
// Javascript program for implementation
// of Lagrange's Interpolation
 
// To represent a data point
// corresponding to x and y = f(x)
class Data
{
    constructor(x,y)
    {
        this.x=x;
        this.y=y;
    }
}
 
// function to interpolate the given
// data points using Lagrange's formula
// xi corresponds to the new data point
// whose value is to be obtained n
// represents the number of known data points
function interpolate(f,xi,n)
{
    let result = 0; // Initialize result
   
    for (let i = 0; i < n; i++)
    {
        // Compute individual terms of above formula
        let term = f[i].y;
        for (let j = 0; j < n; j++)
        {
            if (j != i)
                term = term*(xi - f[j].x) / (f[i].x - f[j].x);
        }
   
        // Add current term to result
        result += term;
    }
   
    return result;
}
 
// Driver code
 // creating an array of 4 known data points
let f=[new Data(0, 2), new Data(1, 3),
                new Data(2, 12), new Data(5, 147)];
 
// Using the interpolate function to obtain
    // a data point corresponding to x=3
document.write("Value of f(3) is : " +
                    interpolate(f, 3, 4));
 
 
// This code is contributed by rag2127
</script>

Producción:

Value of f(3) is : 35

Complejidad:
La complejidad temporal de la solución anterior es O(n ² ) y el espacio auxiliar es O(1).

Referencias:

https://en.wikipedia.org/wiki/Lagrange_polynomial
Matemáticas de ingeniería superior, Dr. BS Grewal
https://mat.iitm.ac.in/home/sryedida/public_html/caimna/interpolation/lagrange.html

Este artículo es una contribución de Ashutosh Kumar . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta