Introducción a la escalada | Inteligencia artificial

Hill Climbing es una búsqueda heurística utilizada para problemas de optimización matemática en el campo de la Inteligencia Artificial. 
Dado un gran conjunto de entradas y una buena función heurística, intenta encontrar una solución suficientemente buena para el problema. Esta solución puede no ser el máximo óptimo global. 

• En la definición anterior, los problemas de optimización matemática implican que la escalada resuelve los problemas en los que necesitamos maximizar o minimizar una función real dada al elegir valores de las entradas dadas. Ejemplo : problema del vendedor ambulante en el que necesitamos minimizar la distancia recorrida por el vendedor.
• ‘Búsqueda heurística’ significa que este algoritmo de búsqueda puede no encontrar la solución óptima al problema. Sin embargo, dará una buena solución en un tiempo razonable.
• Una función heurística es una función que clasificará todas las alternativas posibles en cualquier paso de bifurcación en el algoritmo de búsqueda en función de la información disponible. Ayuda al algoritmo a seleccionar la mejor ruta entre las rutas posibles.

Características de la escalada

1. Variante del algoritmo de generación y prueba: Es una variante del algoritmo de generación y prueba. El algoritmo de generación y prueba es el siguiente: 

1. Generar posibles soluciones. 
2. Pruebe para ver si esta es la solución esperada. 
3. Si se ha encontrado la solución, salga de lo contrario, vaya al paso 1.

Por lo tanto, llamamos Hill Climbing una variante del algoritmo de generación y prueba, ya que toma la retroalimentación del procedimiento de prueba. Luego, el generador utiliza esta retroalimentación para decidir el próximo movimiento en el espacio de búsqueda. 

2. Utiliza el enfoque codicioso : en cualquier punto del espacio de estado, la búsqueda se mueve solo en esa dirección, lo que optimiza el costo de la función con la esperanza de encontrar la solución óptima al final. 

Tipos de escalada 

A. Escalada simple:

Examina los Nodes vecinos uno por uno y selecciona el primer Node vecino que optimiza el costo actual como el siguiente Node. 

Algoritmo para escalar colinas simples :  

Paso 1: Evaluar el estado inicial. Si es un estado objetivo, deténgase y devuelva el éxito. De lo contrario, haga que el estado inicial sea el estado actual. 

Paso 2: Bucle hasta que se encuentre el estado de la solución o no haya nuevos operadores presentes que se puedan aplicar al estado actual. 

a) Seleccione un estado que aún no se haya aplicado al estado actual y aplíquelo para producir un nuevo estado. 

b) Realizar estos para evaluar el nuevo estado 
    i. Si el estado actual es un estado objetivo, deténgase y devuelva el éxito. 
    ii. Si es mejor que el estado actual, conviértalo en el estado actual y continúe. 
    iii. Si no es mejor que el estado actual, entonces continúe en el ciclo hasta encontrar una solución. 

Paso 3: Salir. 
 

B. Ascenso a una colina de ascenso más empinado: 

Primero examina todos los Nodes vecinos y luego selecciona el Node más cercano al estado de la solución a partir del siguiente Node.                                               Algoritmo para la ascensión de la cuesta más empinada:

Paso 1:  Evaluar el estado inicial. Si es un estado objetivo, deténgase y devuelva el éxito. De lo contrario, haga que el estado inicial sea el estado actual. 

Paso 2: repita estos pasos hasta que se encuentre una solución o el estado actual no cambie 

a) Seleccione un estado que aún no se haya aplicado al estado actual.

b) Inicializar un nuevo ‘mejor estado’ igual al estado actual y aplicarlo para producir un nuevo estado.

c) Realizar estos para evaluar el nuevo estado i. Si el estado actual es un estado objetivo, deténgase y devuelva el éxito. ii. Si es mejor que el mejor estado, conviértalo en el mejor estado; de lo contrario, continúe el ciclo con otro estado nuevo.

d) Haga el mejor estado como estado actual y vaya al Paso 2: b) parte.

Paso 3: Salir

C. Escalada estocástica de colinas: 

No examina todos los Nodes vecinos antes de decidir qué Node seleccionar. Simplemente selecciona un Node vecino al azar y decide (según la cantidad de mejora en ese vecino) si se mueve a ese vecino o examina otro. 

       Paso 1:  Evaluar el estado inicial. Si es un estado objetivo, deténgase y devuelva el éxito. De lo contrario, convierta el estado inicial en el estado actual. 

       Paso 2: repita estos pasos hasta que se encuentre una solución o el estado actual no cambie.

       a) Seleccione un estado que aún no se haya aplicado al estado actual.

       b) Aplicar la función sucesora al estado actual y generar todos los estados vecinos .

c) Entre los estados vecinos        generados que son mejores que el estado actual, elija un estado al azar (o basado en alguna función de probabilidad).                                                                                                                           

       d) Si el estado elegido es el estado objetivo, devolver el éxito, de lo contrario, convertirlo en el estado actual y repetir el paso 2: b) parte.

       Paso 3: Salir.
 

Diagrama de espacio de estado para Hill Climbing

El diagrama de espacio de estado es una representación gráfica del conjunto de estados que nuestro algoritmo de búsqueda puede alcanzar frente al valor de nuestra función objetivo (la función que deseamos maximizar). 
Eje X: denota el espacio de estado, es decir, estados o configuración que puede alcanzar nuestro algoritmo. 
Eje Y: denota los valores de la función objetivo correspondientes a un estado particular. 
La mejor solución será aquel espacio de estados donde la función objetivo tenga un valor máximo (máximo global). 

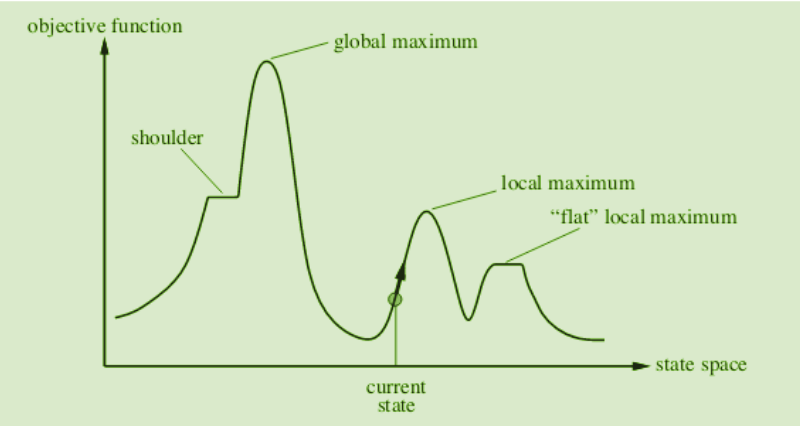
Diferentes regiones en el diagrama de espacio de estado: 

1. Máximo local: es un estado que es mejor que su estado vecino, sin embargo, existe un estado que es mejor que él (máximo global). Este estado es mejor porque aquí el valor de la función objetivo es mayor que sus vecinos. 
    
2. Máximo global: Es el mejor estado posible en el diagrama de espacio de estados. Esto se debe a que, en esta etapa, la función objetivo tiene el valor más alto.
3. Meseta/máximo local plano: Es una región plana del espacio estatal donde los estados vecinos tienen el mismo valor.
4. Ridge: Es una región que es más alta que sus vecinos pero en sí misma tiene una pendiente. Es un tipo especial de máximo local.
5. Estado actual: La región del diagrama de espacio de estado donde estamos presentes actualmente durante la búsqueda.
6. Hombro: Es una meseta que tiene un borde cuesta arriba.

Problemas en diferentes regiones en la escalada

La escalada no puede alcanzar el estado óptimo/mejor (máximo global) si ingresa a alguna de las siguientes regiones:  

1. Máximo local: en un máximo local, todos los estados vecinos tienen un valor peor que el estado actual. Dado que la escalada de colinas utiliza un enfoque codicioso, no se moverá a un estado peor y terminará por sí mismo. El proceso terminará aunque pueda existir una mejor solución. 
   Para superar el problema del máximo local: Utilice la técnica de retroceso . Mantener una lista de los estados visitados. Si la búsqueda llega a un estado no deseado, puede retroceder a la configuración anterior y explorar una nueva ruta.
2. Meseta: En la meseta, todos los vecinos tienen el mismo valor. Por lo tanto, no es posible seleccionar la mejor dirección. 

   Para superar mesetas: Da un gran salto. Seleccione aleatoriamente un estado lejos del estado actual. Lo más probable es que aterricemos en una región sin meseta.

3. Cresta: cualquier punto de una cresta puede parecer un pico porque el movimiento en todas las direcciones posibles es hacia abajo. Por lo tanto, el algoritmo se detiene cuando llega a este estado. 
   Para superar Ridge: en este tipo de obstáculos, use dos o más reglas antes de probar. Implica moverse en varias direcciones a la vez.