Introducción a la transformada de Mojette

Los datos se pueden dividir aproximadamente en dos tipos, que son datos discretos y datos continuos. Los datos discretos solo pueden tomar valores enteros mientras que los datos continuos pueden tomar cualquier valor. El estudio de los objetos geométricos y las propiedades de los datos que son discretos se llama geometría discreta. La geometría discreta tiene varias aplicaciones, su aplicación principal es, por supuesto, la cámara digital y las pantallas.

La transformada de Mojette también utiliza los fundamentos de la geometría discreta. Para entender completamente la transformada de Mojette, debemos entender la transformada de Radon, la transformada de Radon fue desarrollada por johann radon en 1917. La transformada de Radon es un tipo de transformada integral, la inversa de la transformada de Radon se usa para la reconstrucción de imágenes. Varias aplicaciones de la transformada de Radon son ( como se indica en Stanley1993) en el campo de la medicina, la óptica, la astronomía, el análisis de tensión, el magnetismo nuclear.

La transformación de
Mojette: la transformación de Mojette es una forma discreta y exacta de la transformación de radón. Mojette se deriva de una palabra francesa que significa frijoles. La transformada mojette utiliza una geometría discreta para almacenar información en un soporte geométrico discreto. Este soporte es luego proyectado por la transformada de mojette en direcciones discretas. Cuando proyecta suficientes proyecciones, la reconstrucción es posible.

La transformada de Mojette tiene 2 características:

1. Mojette transform solo puede usar sustracciones o sumas para la reconstrucción de la imagen.
2. La transformación utiliza geometría discreta.

La transformada de Mojette se puede explicar matemáticamente usando la siguiente ecuación:

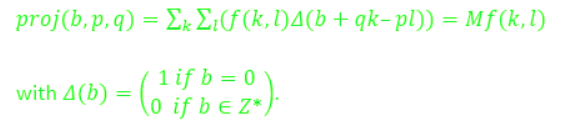
La siguiente figura es un ejemplo de varias direcciones en la transformación de mojette en una cuadrícula de 4*4 con 16 píxeles:

Fantasmas en tomografía discreta:
la transformada de Mojette tiene muchas aplicaciones y, en su mayoría, brinda un resultado único, pero en algunos casos no es posible obtener un resultado único. En tales casos, usamos fantasmas o fantasmas para obtener todas las reconstrucciones posibles de las imágenes que podemos obtener de la transformación de Mojette. En la figura se muestra un ejemplo donde podemos usar fantasma para obtener todas las reconstrucciones posibles cuando el resultado de la transformada de Mojette no es único:

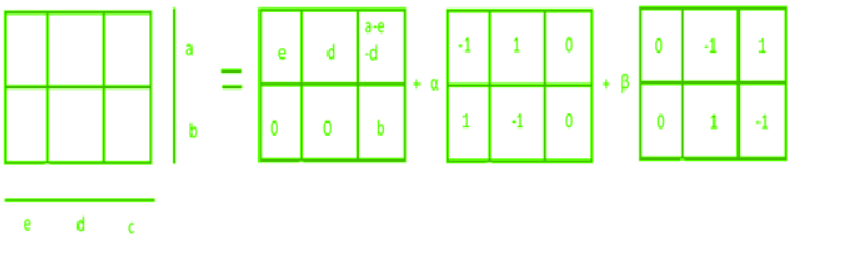
En un lenguaje sencillo, los fantasmas se pueden definir como objetos o ruidos añadidos a la imagen, pero no se pueden ver en las proyecciones de la transformada de Mojette.

Aplicación de fantasmas –

1. Código de corrección de errores
2. Almacenamiento distribuido
3. protocolo de red
4. marca de agua
5. tomografía médica
6. Criptografía de imágenes
7. Imagen de huellas dactilares
8. Distribución de almacenamiento en redes o discos

Ejemplos de fantasmas –

1. Como se ve en la figura siguiente, cuando introducimos un fantasma en la dirección (1,1), es cuando p=1 y q=1. El contenedor correspondiente al fantasma no muestra ningún cambio.

   

2. De manera similar, en la figura siguiente, cuando se introduce un fantasma en la dirección (0,1), es cuando p=0 y q=1. El contenedor correspondiente al fantasma no muestra ningún cambio.

   

3. Los dos ejemplos anteriores son para la proyección única, la Figura 6 muestra un ejemplo de un fantasma de proyección múltiple. En esta figura, tenemos el fantasma cuando las proyecciones son (0,1), (1,1) y (-1,1).