Introducción a las ecuaciones lineales de dos variables en líneas rectas

Las líneas son la configuración más básica en geometría. Muchas otras formas geométricas se pueden obtener de las líneas. Las líneas se refieren a 1-Dimensional. Podemos obtener formas de mayor dimensión usando líneas. Entendamos las líneas en profundidad. Digamos que tenemos dos conjuntos de la siguiente manera,

x = {1, 2, 3, 4, 5, 6, 7}   
y = {10, 20, 30, 40, 50, 60, 70}

Aquí, los puntos en el conjunto y son los valores correspondientes a los puntos en x. Ahora veamos cómo se ve este gráfico

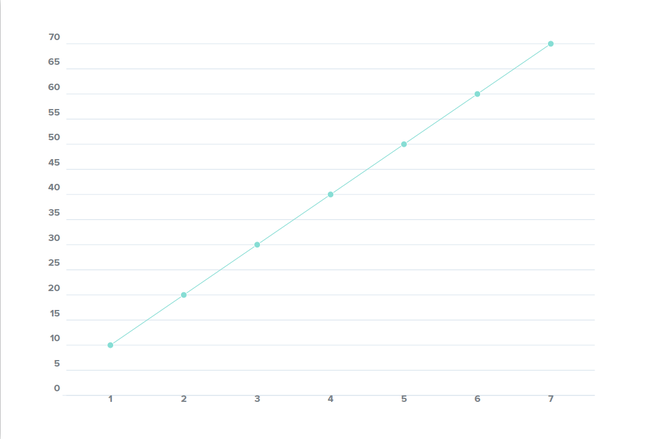
Aquí, teníamos un número limitado de puntos. Ahora piensa, ¿qué pasa si no sabemos cuántos puntos tendremos? Para superar este problema, generalicemos el concepto de líneas. Ahora vamos a definir la ecuación de la recta. Una ecuación general de la recta es 

Dónde:

y = valores en el eje y

x = valores en el eje x

m = pendiente de la línea

c = una constante, intersección matemática en el eje y

Explicación de m (pendiente de la línea)

En palabras matemáticas, es la tan del ángulo formado por la línea con el eje x. Digamos que la recta y = mx + c forma el ángulo theta (θ), entonces la pendiente de esta recta será 

m = tan(θ)

Interpretación de ‘m’

Si m < 0:

Si m es menor que 0, entonces con el aumento del valor de x, el valor de y disminuirá.

Por ejemplo, tomemos una línea x = -2x + 8, donde m = -2 (que es menor que 0) y c = 8 (hablaremos de c más adelante). Entonces el gráfico se verá como, 

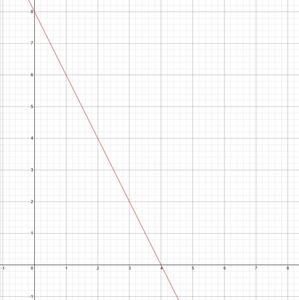
Aquí podemos observar que, con un aumento en x, el valor de y disminuye gradualmente.

Si m > 0:

Si m es mayor que 0, entonces con el aumento del valor de x, el valor de y aumentará. 

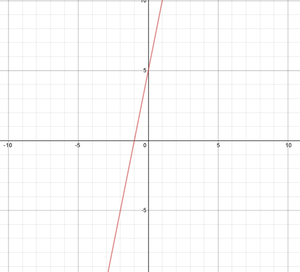
Por ejemplo, tomemos, y = 2x + 8, donde m = 2 y c = 8. Entonces el gráfico se verá así,

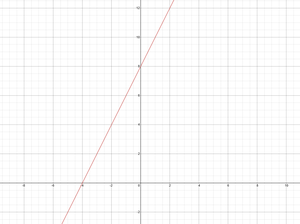
Si m = 0:

En esta condición, el valor de y permanecerá constante con un aumento o disminución en los valores de x. En esta condición, la línea será horizontal (paralela al eje x). Por ejemplo, tomemos y = 5 (también podemos escribir esta ecuación como y = 0x + 5), donde m = 0 y c = 5. Entonces el gráfico se verá así,

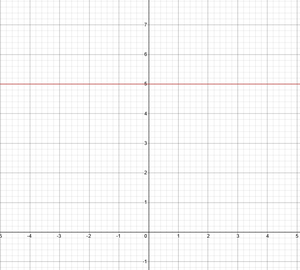
Interpretación de ‘c’

Simplemente yendo al grano,

c es el valor en el eje y, cuando nuestra línea se encuentra con x = 0.

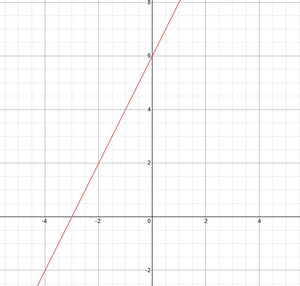
Por ejemplo, tomemos la línea y = -2x + 8. Si ponemos x = 0 (lo que significa que la línea se encuentra con el eje x), entonces nuestra línea se encontrará con el eje y en y = 8. Puede observarlo en el siguiente gráfico .

Tomemos otra línea como y = 2x + 6, luego poner x = 0 dará como resultado que la línea se encuentre con el eje y en y = 8.

La solución de más de una recta son pares de x e y, que satisfacen todas las rectas. “En palabras simples, la solución de líneas es el punto donde se encuentran todas las líneas. Entendámoslo con ejemplos.

Ejemplo 1: 

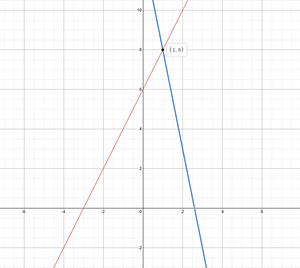
Digamos que tenemos dos líneas. 

y = 2x + 6 ———— (1)

y = -5x + 13 ———— (2)

Si dibujamos estas líneas en un plano y encontramos un punto donde ambas líneas se encuentran, entonces será (1,8). (Asegúrese de que la solución de líneas es uno y solo un punto donde se encuentran todas las líneas). Echemos un vistazo a la gráfica.

Ahora, no tendremos tiempo de dibujar las gráficas de cada línea dada. Deberíamos tener algún método en papel para encontrar la solución de líneas. Entendamos el enfoque en papel. De las líneas anteriores (1) y (2), elijamos una línea como línea de base (digamos que la línea de base es (1).)

La línea base es y = 2x + 6

Tenemos variables x e y en ambas líneas, así que ahora lo que haremos, elegiremos nuestra segunda línea y pondremos el RHS (lado derecho) de esa segunda línea (2) en la línea (1) en el lugar de y . Así que nuestra ^primera línea se convertirá en,

-5x + 13 = 2x + 6

Resolviendo esta ecuación, obtenemos

X = 1

Ahora, poniendo este x = 1 en cualquiera de las dos líneas anteriores, obtendremos el valor de la y. Pongamos x = 1 en la línea (1).

y = 2x + 6

y = 2 × 1 + 6
y = 8

Entonces, ahora tenemos un par de valores (x, y) = (1, 8).

Aquí, observe que obtenemos solo un punto en el plano que es la única solución de la línea.

Puede aplicar este método a cualquier par de líneas para obtener la solución de líneas.

Ejemplo: 2

Digamos que tenemos dos líneas. 

y = x + 9 ———————— (1)

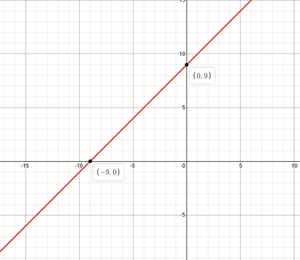
y

y = 5x + 5 ———————— (2)

Ahora poniendo el valor de y de la ecuación-1 (es decir, x + 9) en la ecuación-2, obtenemos

∴ y = 5x + 5

∴ x + 9 = 5x + 5

∴ 4x = 4

∴ x = 1

Ahora obtenemos x = 1, poniendo este valor de x en cualquiera de las dos ecuaciones (pongamos en la ecuación-2), obtenemos,

∴ y = 5x + 5

∴ y = 5 × 1 + 5

∴ y = 10

Entonces, la solución de las líneas 1 y 2 es (x, y) = (1, 10). Puede cotejar, estamos obteniendo la misma respuesta si ponemos el valor de x en la ecuación-1. Echa un vistazo a la gráfica.

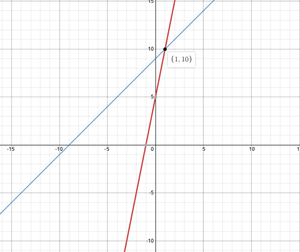
¡Hurra! Obtenemos la respuesta correcta. Concretemos este concepto tomando un último ejemplo (algo complicado).

Ejemplo 3:

Tomemos líneas,

x = 2y + 5 —————— (1) y

y = 2x + 5 —————— (2)
 

Aquí, poner el valor de x de la ecuación-1 en la ecuación-2 conducirá a cálculos fáciles. Así que pongamos x = 2y + 5 (ecuación-1) en la ecuación-2.

∴ y = 2 (2y + 5) + 5

∴ y = 4 × y + 15

∴ -3 × y = 15

∴ y = -5

Para encontrar el valor de x, pongamos y = -5 en la ecuación-1,

∴ x = 2y + 5

∴ x = 2 × (-5) + 5

∴ x = -5

Entonces, la solución de las líneas 1 y 2 es (x,y) = (-5,-5). Trate de encontrar la pendiente de la línea 1 en este ejemplo. Será (1/2). Trate de trazar el gráfico usted mismo y vea si su respuesta coincide con esta respuesta o nota.