Introducción a las Redes Neutrales Artificiales

El aprendizaje de ANN es resistente a los errores en los datos de entrenamiento y se ha aplicado con éxito para aprender funciones con valores reales, valores discretos y valores vectoriales que contienen problemas como la interpretación de escenas visuales, el reconocimiento de voz y el aprendizaje de estrategias de control de robots. El estudio de las redes neuronales artificiales (ANN) se inspiró en parte en la observación de que los sistemas de aprendizaje biológico están construidos a partir de redes muy complejas de neuronas interconectadas en el cerebro. El cerebro humano contiene una red densamente interconectada de aproximadamente 10^11-10^12 neuronas, cada neurona conectada, en promedio, a 10^4-10^5 otras neuronas. Entonces, en promedio, el cerebro humano tarda aproximadamente 10 ^ -1 para tomar decisiones sorprendentemente complejas. Los sistemas ANN están motivados para capturar este tipo de computación altamente paralela basada en representaciones distribuidas. En general,
Pero las ANN están menos motivadas por los sistemas neuronales biológicos, existen muchas complejidades en los sistemas neuronales biológicos que no están modeladas por ANN. Algunos de ellos se muestran en las figuras.

Diferencia entre neuronas biológicas y neuronas artificiales

neuronas biológicas	neuronas artificiales
Componentes principales: axiones, dendritas, sinapsis	Componentes principales: Nodes, entradas, salidas, ponderaciones, sesgo
La información de otras neuronas, en forma de impulsos eléctricos, ingresa a las dendritas en puntos de conexión llamados sinapsis. La información fluye desde las dendritas hasta la célula donde se procesa. La señal de salida, un tren de impulsos, luego se envía por el axón a la sinapsis de otras neuronas.	Los arreglos y conexiones de las neuronas forman la red y tienen tres capas. La primera capa se llama capa de entrada y es la única capa expuesta a señales externas. La capa de entrada transmite señales a las neuronas de la siguiente capa, que se denomina capa oculta. La capa oculta extrae características o patrones relevantes de las señales recibidas. Aquellas características o patrones que se consideran importantes se dirigen luego a la capa de salida, que es la capa final de la red.
Una sinapsis puede aumentar o disminuir la fuerza de la conexión. Aquí es donde se almacena la información.	Las señales artificiales se pueden cambiar por pesos de manera similar a los cambios físicos que ocurren en las sinapsis.
Aproximadamente 10 ¹¹ neuronas.	10 ² – 10 ⁴ neuronas con tecnología actual

Diferencia entre el cerebro humano y las computadoras en términos de cómo se procesa la información.

Cerebro humano (Red de neuronas biológicas)	Computadoras (Red de neuronas artificiales)
El cerebro humano funciona de forma asíncrona	Las computadoras (ANN) funcionan sincrónicamente.
Las neuronas biológicas calculan lentamente (varios ms por cálculo)	Las neuronas artificiales calculan rápido (<1 nanosegundo por cálculo)
El cerebro representa la información de forma distribuida porque las neuronas no son fiables y podrían morir en cualquier momento.	En los programas de computadora, cada bit tiene que funcionar según lo previsto, de lo contrario, estos programas fallarían.
Nuestro cerebro cambia su conectividad con el tiempo para representar nueva información y requisitos que se nos imponen.	La conectividad entre los componentes electrónicos de una computadora nunca cambia a menos que reemplacemos sus componentes.
Las redes neuronales biológicas tienen topologías complicadas.	Las ANN suelen estar en una estructura de árbol.
Los investigadores aún deben descubrir cómo aprende realmente el cerebro.	Las ANN usan Gradient Descent para el aprendizaje.

Ventaja de usar redes neuronales artificiales:

El problema en las ANN puede tener instancias que están representadas por muchos pares de atributos y valores.
Las ANN utilizadas para problemas que tienen la salida de la función objetivo pueden ser de valor discreto, de valor real o un vector de varios atributos de valor real o discreto.
Los métodos de aprendizaje de ANN son bastante resistentes al ruido en los datos de entrenamiento. Los ejemplos de entrenamiento pueden contener errores que no afectan el resultado final.
Se utiliza generalmente cuando se requiere una evaluación rápida de la función objetivo aprendida.
Las ANN pueden soportar largos tiempos de entrenamiento dependiendo de factores como la cantidad de pesos en la red, la cantidad de ejemplos de entrenamiento considerados y la configuración de varios parámetros del algoritmo de aprendizaje.

El modelo de neurona de McCulloch-Pitts: Warren McCulloch
y Walter Pitts introdujeron el primer modelo de una neurona artificial en 1943. El modelo neuronal de McCulloch-Pitts también se conoce como puerta de umbral lineal. Es una neurona de un conjunto de entradas I1, I2,…, Im y una salida y. La puerta de umbral lineal simplemente clasifica el conjunto de entradas en dos clases diferentes. Por lo tanto, la salida y es binaria. Tal función se puede describir matemáticamente usando estas ecuaciones:

$\newline Sum = \sum_{i=1}^{N}I_iW_i, \newline y = f(Sum)$

W1, W2, W3….Wn son valores de peso normalizados en el rango de (0,1) o (-1,1) y asociados con cada línea de entrada, Sum es la suma ponderada y es una constante de umbral. La función f es una función de paso lineal en el umbral

Redes neuronales de una sola capa (perceptrones)
La entrada es multidimensional (es decir, la entrada puede ser un vector):
entrada x = (I1, I2, .., In)
Los Nodes (o unidades) de entrada están conectados (típicamente completamente) a un Node (o múltiples Nodes) en la siguiente capa. Un Node en la siguiente capa toma una suma ponderada de todas sus entradas:
$\newline Summed Input = \sum_{i}w_iI_i \newline$

La regla:
el Node de salida tiene un «umbral» t.
Regla: si se sumó la entrada? t, luego «dispara» (salida y = 1). De lo contrario (entrada sumada < t) no se dispara (salida y = 0).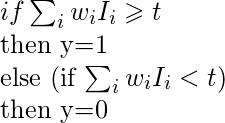
$\newline if \sum_{i}w_iI_i\geqslant t then y=1 \newline else (if \sum_{i}w_iI_i < t) then y=0 \newline$ cual

Limitaciones de los perceptrones:
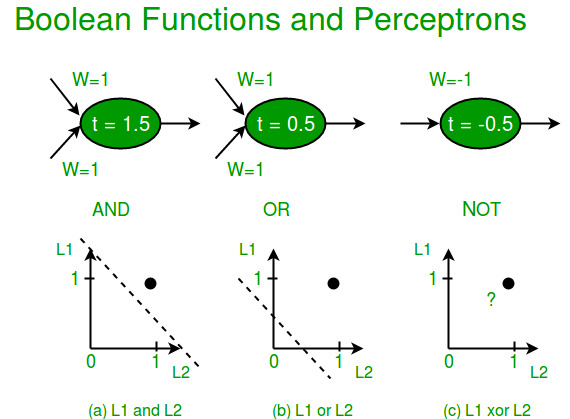
(i) Los valores de salida de un perceptrón pueden tomar solo uno de dos valores (0 o 1) debido a la función de transferencia de límite estricto.
(ii) Los perceptrones solo pueden clasificar conjuntos de vectores linealmente separables. Si se puede dibujar una línea recta o un plano para separar los vectores de entrada en sus categorías correctas, los vectores de entrada son linealmente separables. Si los vectores no son linealmente separables, el aprendizaje nunca llegará a un punto en el que todos los vectores se clasifiquen correctamente.
La función booleana XOR no es linealmente separable (sus instancias positivas y negativas no pueden separarse por una línea o un hiperplano). Por lo tanto, un perceptrón de una sola capa nunca puede calcular la función XOR. Este es un gran inconveniente que una vez resultó en el estancamiento del campo de las redes neuronales. Pero esto se ha resuelto mediante multicapa.

Redes neuronales multicapa
Un perceptrón multicapa (MLP) o red neuronal multicapa contiene una o más capas ocultas (además de una capa de entrada y otra de salida). Mientras que un perceptrón de una sola capa solo puede aprender funciones lineales, un perceptrón de varias capas también puede aprender funciones no lineales.

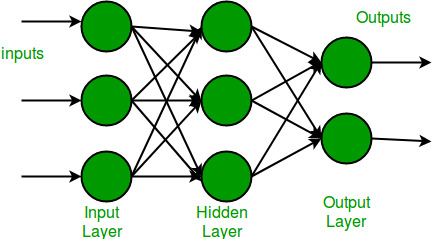
Esta neurona toma como entrada x1,x2,….,x3 (y un término de sesgo +1) y emite f(entradas sumadas+sesgo), donde f(.) se denomina función de activación. La función principal de Bias es proporcionar a cada Node un valor constante entrenable (además de las entradas normales que recibe el Node). Cada función de activación (o no linealidad) toma un solo número y realiza una cierta operación matemática fija sobre él. Hay varias funciones de activación que puede encontrar en la práctica:

Sigmoid: toma la entrada de valor real y la reduce al rango entre 0 y 1.
$\newline \sigma(x) = \frac{1}{(1+exp(-x))} \newline$
tanh: toma la entrada de valor real y la reduce al rango [-1, 1].
$\newline tanh(x) = 2\sigma( 2x ) -1 \newline$
ReLu: ReLu significa Unidades Lineales Rectificadas. Toma una entrada de valor real y la umbraliza a 0 (reemplaza los valores negativos a 0).
$\newline f(x) = max(0,x) \newline$