Introducción a Señales y Sistemas: Propiedades de los sistemas

La señal es una corriente eléctrica o electromagnética que transporta datos, que puede transmitirse o recibirse.

Representado matemáticamente en función de una variable independiente, por ejemplo, densidad, profundidad, etc. Por lo tanto, una señal es una cantidad física que varía con el tiempo, el espacio o cualquier otra variable independiente mediante la cual se pueda transmitir información. Aquí la variable independiente es el tiempo.

Tipos de señales de tiempo:

Señales de tiempo continuas x(t)- definidas en cada punto en el tiempo
Señales de tiempo discretas x[n]: definidas solo en un conjunto discreto de valores de tiempo ( entero ).

Un sistema es cualquier conjunto físico de componentes o una función de varios dispositivos que toma una señal de entrada y produce una señal de salida.

Cálculo de energía y potencia de señales:

Energía : cuadrado de amplitud/magnitud (si es complejo) en todo el dominio del tiempo.

para una señal de tiempo continuo-

$E=\int_{-\infty}^{\infty} |x(t)|^2 dt$

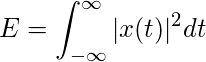
para una señal de tiempo discreto-

$E=\sum_{-\infty}^{\infty} |x[n]|^2$

Potencia- Tasa de cambio de energía.

para una señal de tiempo continuo.

$P=\lim_{T\to\infty} 1/(2T) (\int_{-T}^{T} |x(t)|^2 dt)$

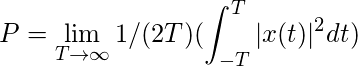
para una señal de tiempo discreto-

$P=\lim_{N\to\infty} 1/(2N+1) (\sum_{-N}^{N} |x[n]|^2)$

Clases de señales en función de su potencia y energía:

Señal de energía : generalmente señales convergentes, señales aperiódicas o señales limitadas.
$E < \infty\ and\ P=0$
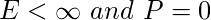
Señal de potencia : generalmente señales periódicas, ya que abarcan un área infinita bajo su gráfico y se extienden desde 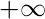$+\infty$ hasta $-\infty$ .
$E \rightarrow \infty\ and\ P=constant$
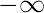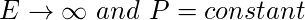
Ni energía ni señal de potencia
$E \rightarrow \infty\ and\ P \rightarrow \infty$

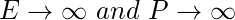
Transformación de la variable independiente:

Desplazamiento : la señal se puede retrasar (x(tT)) o adelantar (x(t+T)) incrementando o decrementando la variable independiente (tiempo aquí).
La forma del gráfico sigue siendo la misma, solo cambiada en el eje del tiempo.
Escalado: la señal se puede comprimir (x(at), a>1) o expandir (x(t/a), a>1 o x(at), 1>a>0).
Aquí, la forma/comportamiento del gráfico de la señal cambia a medida que cambia el período de tiempo fundamental. En compresión el período de tiempo disminuye y en expansión el período de tiempo aumenta.
Inversión : también llamado plegado, ya que el gráfico se pliega sobre el eje Y o T si se da x (Tt).

Propiedades de los sistemas:

Periodicidad : el comportamiento/gráfico de la señal se repite después de cada T. Por lo tanto,
$x(t)=x(t+nT)\ or\ x(t)=x(t-nT)$

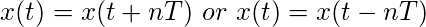
aquí T es el período fundamental
Entonces podemos decir que la señal permanece sin cambios cuando se desplaza por múltiplos de T.
Par e impar: una señal par es simétrica con respecto al eje Y.
x(t)=x(-t) par
x(t)=-x(-t) impar
Una señal se puede dividir en partes pares e impares para facilitar ciertas conversiones.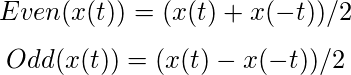
Linealidad- constituye de dos propiedades-
(i) Aditividad/Superposición:
si x1(t) -> y1(t)
y x2(t) -> y2(t)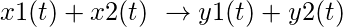

$x1(t) + x2(t)\ \rightarrow y1(t) + y2(t)$

(ii) Propiedad de escalar:
si x1(t) -> y1(t)
entonces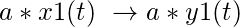

$a*x1(t)\ \rightarrow a*y1(t)$

Si ambos se cumplen, el sistema es lineal.
Invariante en el tiempo: cualquier retraso proporcionado en la entrada debe reflejarse en la salida para un sistema invariante en el tiempo.
$take \ x2(t)=x(t-T)$$$$then\ y(x2(t))\ must\ be\ =x2(y(t))$

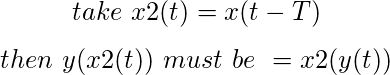
aquí x2(t) es una entrada retardada.
Comprobamos si poner una entrada retrasada en el sistema es lo mismo que retrasar la señal de salida.
Sistemas LTI : un sistema lineal invariante en el tiempo. Un sistema que es lineal e invariante en el tiempo.
Estabilidad BIBO: la estabilidad de salida limitada de entrada limitada.
Decimos que un sistema es BIBO estable si-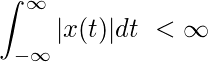
$\int_{-\infty}^{\infty} |x(t)| dt\ < \infty$
Causalidad : las señales causales son señales que son cero para todo tiempo negativo.
Si algún valor de la señal de salida depende de un valor futuro de la señal de entrada, entonces la señal no es causal.

Publicación traducida automáticamente

Artículo escrito por arya31 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta