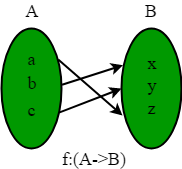
Una relación es básicamente un conjunto o combinación de conjuntos solicitados. Un par arreglado, normalmente llamado como un punto. Una relación es un grupo de pares de valores de entrada y salida, que se muestra en un par ordenado.
Es una interrelación entre conjuntos de datos.
Una relación = (valor de entrada, valor de salida)
Considere este ejemplo de una relación: La relación entre los colores favoritos de los estudiantes y sus nombres.
(x, y) = (nombre del estudiante, color favorito)
Conjunto A = {(Rosa, Casarse), (Verde, Ron), (Rojo, Steve), (Rojo, Paul), (Rosa, Daemon)}
Observe el conjunto con atención, el mismo color es amado por más de un estudiante. Por lo tanto, también permiten que un valor de entrada tenga más de un valor de salida correspondiente.
Función
Una función es un conjunto de pares ordenados donde cada componente de entrada tiene solo UN componente de salida relacionado con él.
El ejemplo anterior de una relación no es una función porque el mismo color gusta a más de un alumno.
Como una misma entrada está asociada a más de una salida, NO puede ser una función.
Nota: una función puede tener dos valores de entrada asignados al mismo valor de salida, pero NO puede tener dos valores de salida asignados al mismo valor de entrada.
| ES UNA FUNCIÓN | NO ES UNA FUNCIÓN |
|
{ (1,5) , (4,5) } |
{ (5,1) , (5,4) } |

Intervalo y su notación
El Intervalo son subconjuntos que se presentarán en la recta numérica.
Ejemplo: Todos los números reales en el rango de 1 y 6 es un intervalo como 2.5, 3, 4.567, y así sucesivamente hasta 6.
¿Incluimos 1 y 6 en el intervalo?
La notación de intervalo es un método para componer subconjuntos de la recta numérica real.
Ejemplo : (0, 20], [1, 2], (4, 7), [4, 8), [-3, 0].
Tipos de intervalo
Hay dos tipos de intervalos en una recta numérica:
- Intervalo abierto
- Intervalo cerrado
Intervalo abierto no incluye los puntos finales en el conjunto. ( ) los corchetes representan el intervalo abierto.
Ejemplo: (4, 6), (6, 9), (-3, 2)
El intervalo cerrado incluye los puntos finales del conjunto. Se representa mediante corchetes [ ].
Ejemplo: [3, 5], [-4, 0], [6, 9]
Ejemplo – Establecer A= {x : -4 < x <= 5 }. Aquí 4 no está incluido en el conjunto pero 5 está incluido como x.
Entonces, el conjunto se representa como x = (-4,5).
Dominio y rango
Dominio : todos los valores que entran en una relación o función se denominan dominio.
Rango : todas las entidades ( salida ) que surgen de una relación o una función se denominan rango.
Todos los valores de entrada que se utilizan ( valores independientes ) forman el conjunto de Dominio.
Todos los valores de salida que se utilizan ( valores dependientes ) forman el conjunto Rango.
Ejemplo: función dada: – f = 2x+1, encuentra el dominio, rango si 1<=x<=5.
Solución:
Los valores de x están entre 1 y 10.
Entonces, el dominio es {1, 2, 3, 4, 5} .
Los valores de f obtenidos al poner elementos de dominio en la función serán rango.
Entonces, si x=1 entonces f = 2(1)+1 = 3,
si x=2 entonces f = 2(2)+1 = 5,
si x=3 entonces f = 2(3)+1 =7,
si x=4 entonces f = 2(4)+1 = 9,
si x=5 entonces f = 2(5)+1 = 11.
Entonces, el rango es {3,5,7,9,11} .
Ejemplo: Función dada: – F = x 2 -5 , ¿Encuentra el dominio, el rango?
Solución:
El valor de x se eleva al cuadrado y luego 5 se resta por 5. Cualquier número real se puede elevar al cuadrado y se le puede restar 5, por lo que no hay restricciones en el dominio de esta función. El dominio es el conjunto de los números reales. La forma de intervalo del conjunto de dominios será (-∞,∞).
Ejemplo: Función dada: – F= (x+1)/(1-x), ¿Encontrar el dominio?
Solución:
Aquí, el denominador está presente en la función, por lo que debemos restringir nuestra entrada para que el denominador no se convierta en cero. entonces, encontramos el valor de x donde el denominador será cero al igualarlo con 0.
1-x = 0
1 = x
X = 1
Entonces, excluiremos 1 de nuestro conjunto de dominios. El conjunto de dominios son todos los números reales excepto 1 . La forma de intervalo del conjunto de dominios será (-∞,1)∪(1,∞). donde ∪ es símbolo de unión.
Dominio y rango en un gráfico
En un gráfico, las coordenadas x (abscisas) son el dominio y las coordenadas y (las coordenadas) son el rango.
La abscisa es el valor del dominio, cuando lo ponemos en la función, el valor que obtenemos como salida estará en el eje y.
Ejemplo: En la figura dada, la línea y=1 es una función donde todos los valores de x pertenecen al conjunto de dominio y para cada valor de x, obtenemos solo 1 como respuesta. Entonces, 1 es el rango.

Ejemplo: Encuentra el dominio y rango de la función f(x) = x 2 donde -1<x<1.
Solución:
Como se indica en el ejemplo, x tiene una restricción de -1 a 1, por lo que el dominio de la función en forma de intervalo es (-1,1) .
Los valores de dominio son abscisas y como f es una función de x entonces, los valores de f (ordenadas) que obtenemos al poner valores de abscisas formarán nuestro rango. Es difícil encontrar el valor de y manualmente para cada x, por lo que será fácil si dibujamos un gráfico y encontramos el rango (salida) de la función.

Sabemos que la salida es un valor positivo para la función que incluye 0 y excluye 1. Del gráfico, podemos concluir que el rango de la función en forma de intervalo es [0, 1).
Nota: Como el valor de x para el que obtenemos 1 como resultado no está incluido en el dominio, no incluimos 1 en el rango.
No usamos corchetes ‘[‘ o ‘]’ en el dominio ya que -1 y 1 no están incluidos para el valor de x. Y usamos ‘[‘ para 0 ya que está incluido en los valores de rango.
¿Qué es Co-Dominio?
El Conjunto en el que los elementos pueden salir como salida se denomina Co-dominio.
Los elementos que son el valor de salida al dar entrada a la función forman un conjunto llamado Rango.
Todos los elementos que son posibles como salida pero no el resultado de los elementos de función y rango juntos forman un conjunto llamado Co-dominio.
Ejemplo: Dada una función y = 2x y dado si x>=1 , x<=7.
Entonces, Conjunto A = { 1,2,3,4,5,6,7} es dominio,
Establecer B = {2,4,6,8,10,12,14} es rango,
Establecer C = { 1,2,4,6,7,8,10,12,14,15} o {todos los números reales} es codominio.
Importancia del codominio
¿La raíz cuadrada es una función? NO, porque cuando ponemos 16 como entrada, obtenemos 4,-4 como salida.
Sabemos que la función tiene un solo valor y no podemos obtener dos valores de una entrada. Pero si definimos el codominio como todos los enteros positivos, el rango se limitará a los enteros positivos.
Por lo tanto, solo 4 se considerarán como salida. Entonces, la raíz cuadrada será una función si el codominio está definido o limitado.
Co-Domain afecta si la relación dada es una función o no.
Relación y función en un gráfico
Como sabemos que las coordenadas x son dominio y las coordenadas y son rango, entonces solo se permite un valor de y para cualquier valor x, entonces solo la curva o relación se considerará como una función.
Prueba de línea vertical para verificar funciones: si cualquier línea vertical puede encontrar el contorno de una relación en solo UN punto, entonces la conexión se llama función.
Si cualquier línea vertical se cruza con cualquier gráfico de una relación en más de un valor, entonces esa relación no se puede decir como una función.
Aquí, en la siguiente figura, la línea (y=c), donde c es cualquier constante, es una función, ya que cualquier línea vertical puede cruzarse con la línea horizontal en un solo punto.

Este gráfico de la parábola no se considera como una función ya que una línea vertical intersecta este gráfico en dos puntos.
tipos de relaciones
- relación universal
- Relación vacía
- Relación de identidad
- relación simétrica
- Relación inversa
- Relación reflexiva
- Relación transitiva
Relaciones universales:
Una relación se denomina conexión universal si cada componente de un conjunto se identifica entre sí.
Considere el conjunto A = {a, b, c}. Las relaciones universales serán R si R = {m, n} donde, |mn| ≥ 0.
Relaciones vacías:
La relación en la que no hay conexión entre los componentes de un conjunto. Una relación vacía también se llama relación nula.
Considere si el conjunto A = {2, 3} entonces, la relación nula es R = {m,n} donde, |mn| = 8.
Relaciones de identidad:
La relación donde cada componente de un conjunto se identifica consigo mismo
Considere un conjunto A = {1,2,3}, la relación de identidad será I = {1,1}, {2,2}, {3,3}. yo = {(m,m), m ∈ A}
Relaciones simétricas:
Una relación es simétrica si a=b se cumple, entonces b=a también se cumple. Una conexión R es simétrica solo si (b, a) ∈ R es genuina cuando (a,b) ∈ R.
R = {(1, 2), (2, 1)} es un conjunto de relaciones simétricas para un conjunto A = {1, 2}.
Relaciones inversas:
La relación inversa ocurre cuando un conjunto tiene pares inversos de otro conjunto.
Considere si el conjunto A = {(1,2),(3,4)}, entonces la relación inversa será R-1 = {(2,1), (4,3)}. R-1 = {(n, m): (m, n) ∈ R}
Relaciones reflexivas:
Una relación donde cada componente se encuentra a sí mismo.
Para el conjunto A = {-1, 4}. Relación reflexiva = R = {(-1, -1), (4, 4), (-1, 4), (4, -1)}. (x,x) ∈ R
Relaciones transitivas:
Si (m,n) ∈ R, (n,p) ∈ R, entonces (m,p) ∈ R.
Considere aRb y bRc ⇒ aRc ∀ a, b, c ∈ A
Publicación traducida automáticamente
Artículo escrito por apoorvadaga y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA