Intuición de Adam Optimizer

Prerrequisitos:  Técnicas de optimización en Gradient Descent

Adam optimizador 

Adaptive Moment Estimation es un algoritmo para la técnica de optimización del descenso de gradiente. El método es realmente eficiente cuando se trabaja con un gran problema que involucra una gran cantidad de datos o parámetros. Requiere menos memoria y es eficiente. Intuitivamente, es una combinación del algoritmo de ‘descenso de gradiente con impulso’ y el algoritmo ‘RMSP’.

¿Cómo funciona Adán?

El optimizador de Adam implica una combinación de dos metodologías de descenso de gradiente: 

Impulso: 

Este algoritmo se utiliza para acelerar el algoritmo de descenso del gradiente teniendo en cuenta el «promedio ponderado exponencialmente» de los gradientes. El uso de promedios hace que el algoritmo converja hacia los mínimos a un ritmo más rápido. 

dónde,

mt = aggregate of gradients at time t [current] (initially, mt = 0)
mt-1 = aggregate of gradients at time t-1 [previous]
Wt = weights at time t
Wt+1 = weights at time t+1
αt = learning rate at time t 
∂L = derivative of Loss Function
∂Wt = derivative of weights at time t
β = Moving average parameter (const, 0.9)

Propagación de raíz cuadrática media (RMSP): 

Root mean square prop o RMSprop es un algoritmo de aprendizaje adaptativo que intenta mejorar AdaGrad. En lugar de tomar la suma acumulada de gradientes cuadrados como en AdaGrad, toma el ‘promedio móvil exponencial’.

dónde, 

Wt = weights at time t
Wt+1 = weights at time t+1
αt = learning rate at time t 
∂L = derivative of Loss Function
∂Wt = derivative of weights at time t
Vt = sum of square of past gradients. [i.e sum(∂L/∂Wt-1)] (initially, Vt = 0)
β = Moving average parameter (const, 0.9)
ϵ = A small positive constant (10-8)

NOTA: El tiempo (t) podría interpretarse como una iteración (i) . 

Adam Optimizer hereda las fortalezas o los atributos positivos de los dos métodos anteriores y se basa en ellos para brindar un descenso de gradiente más optimizado. 

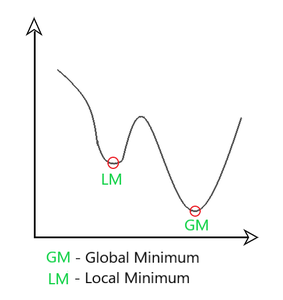
Aquí, controlamos la tasa de descenso del gradiente de tal manera que hay una oscilación mínima cuando alcanza el mínimo global mientras toma pasos lo suficientemente grandes (tamaño de paso) para pasar los obstáculos mínimos locales en el camino. Por lo tanto, combina las características de los métodos anteriores para alcanzar el mínimo global de manera eficiente. 

Aspecto matemático de Adam Optimizer

Tomando las fórmulas utilizadas en los dos métodos anteriores, obtenemos

Parameters Used :
1. ϵ = a small +ve constant to avoid 'division by 0' error when (vt -> 0). (10-8)
2. β1 & β2 = decay rates of average of gradients in the above two methods. (β1 = 0.9 & β2 = 0.999)
3. α — Step size parameter / learning rate (0.001)

Dado que m _t y v _t se han inicializado como 0 (basado en los métodos anteriores), se observa que tienen una tendencia a estar ‘sesgados hacia 0’ ya que tanto β ₁ como β ₂ ≈ 1. Este optimizador soluciona este problema al calculando m _t y v _t ‘corregidos por sesgo’ . Esto también se hace para controlar los pesos mientras se alcanza el mínimo global para evitar altas oscilaciones cuando se está cerca de él. Las fórmulas utilizadas son:

Intuitivamente, nos estamos adaptando al descenso del gradiente después de cada iteración para que permanezca controlado e imparcial durante todo el proceso, de ahí el nombre Adam. 

Ahora, en lugar de nuestros parámetros de peso normales m _t y v _t , tomamos los parámetros de peso con corrección de sesgo (m_hat) _t y (v_hat) _t . Poniéndolos en nuestra ecuación general, obtenemos

Actuación:

Sobre la base de las fortalezas de los modelos anteriores, el optimizador de Adam brinda un rendimiento mucho mayor que el utilizado anteriormente y los supera por un gran margen al brindar un descenso de gradiente optimizado. El gráfico que se muestra a continuación muestra claramente cómo Adam Optimizer supera al resto del optimizador por un margen considerable en términos de costo de capacitación (bajo) y rendimiento (alto). 

Comparación de rendimiento en el costo de capacitación