Inverso de una fórmula matricial

Una array es un arreglo rectangular de números enteros que se divide en filas y columnas. Es un conjunto de números enteros que se organizan en un número definido de filas y columnas. El número de filas y columnas en una array se conoce como su dimensión u orden. Una array se ilustra mediante la array de números enteros a continuación. 

Por convención, las filas se enumeran primero, seguidas de las columnas. Así, el tamaño (u orden) de la array anterior es 4 x 3, lo que indica que contiene 4 filas y 3 columnas. Los elementos de la array son números que aparecen en las filas y columnas de una array. El elemento de la primera columna de la primera fila de la array anterior es 1; el elemento de la segunda columna de la primera fila es 2; y así.

Inversa de una array

La inversa de una array es otra array que, cuando se multiplica por la array dada, produce la identidad multiplicativa. Para una array A y su inversa de A ^-1 , la propiedad de identidad se cumple.

AA ^-1 = A ^-1 A = I, donde I es la array identidad.

Terminología básica

La terminología que se enumera a continuación puede ayudarlo a comprender el inverso de una array de manera más clara y sencilla.

• Menor: El menor se define para cada elemento de la array. El determinante producido después de eliminar la fila y la columna que contiene este elemento es el menor de ese elemento. Para una array  , el menor del primer elemento 1 es,  .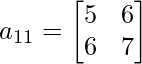
• Cofactor: El cofactor de un elemento se calcula multiplicando el menor con -1 por el exponente de la suma de los elementos de fila y columna en la representación del orden del elemento.

Cofactor de a _ij = (-1) ^i+j M _ij , donde M _ij es el menor de ese elemento

• Determinante: El determinante de la array es igual a la suma del producto de los elementos y sus cofactores de una fila o columna específica de la array.
• Adjunto de Matrix: El adjunto de una array es la transpuesta de la array del elemento cofactor de la array.

Inverso de una fórmula matricial

La inversa de la array A, es decir, A ^-1 , se calcula mediante la fórmula de la inversa de la array, que consiste en dividir el adjunto de una array por su determinante. 

dónde,

adj A = adjunto de la array A

|A| = determinante de la array A

La inversa de una array A se puede calcular siguiendo los pasos a continuación:

Paso 1: Determinar los menores de todos los elementos A.

Paso 2: Luego, calcule los cofactores de todos los elementos y construya la array de cofactores sustituyendo los elementos de A con sus respectivos cofactores.

Paso 3: Tome la transpuesta de la array cofactor de A para encontrar su adjunto (escrito como adj A).

Paso 4: Multiplica adj A por el recíproco del determinante.

Ejemplo: Encuentra la inversa de la array   usando la fórmula.

Tenemos, 

Encuentre el adjunto de la array A calculando los cofactores de cada elemento y luego obteniendo la transpuesta de la array del cofactor.

adj A = 

Encuentre el valor del determinante de la array.

|A| = 4(18–25) – 3(54–5) + 8(30–2)

= 49

Entonces, la inversa de la array es,

A ^–1 = 

= 

Problemas de muestra

Pregunta 1. Encuentra la inversa de la array   usando la fórmula.

Solución:

Tenemos,

Encuentre el adjunto de la array A calculando los cofactores de cada elemento y luego obteniendo la transpuesta de la array del cofactor.

adj A = 

Encuentre el valor del determinante de la array.

|A| = 2(4–6) – 3(4–4) + 1(3–2)

= –3

Entonces, la inversa de la array es,

A ^–1 = 

= 

Pregunta 2. Encuentra la inversa de la array A=  usando la fórmula.

Solución:

Tenemos,

A=

Encuentre el adjunto de la array A calculando los cofactores de cada elemento y luego obteniendo la transpuesta de la array del cofactor.

adj A = 

Encuentre el valor del determinante de la array.

|A| = 6(0–4) – 2(0–8) + 3(0–0)

= 16

Entonces, la inversa de la array es,

A ^–1 = 

= 

Pregunta 3. Encuentra la inversa de la array A=  usando la fórmula.

Solución:

Tenemos,

A=

Encuentre el adjunto de la array A calculando los cofactores de cada elemento y luego obteniendo la transpuesta de la array del cofactor.

adj A = 

Encuentre el valor del determinante de la array.

|A| = 1(1–0) – 2(0–0) + 3(0–0)

= 1

Entonces, la inversa de la array es,

A ^–1 = 

= 

Pregunta 4. Encuentra la inversa de la array A=  usando la fórmula.

Solución:

Tenemos,

A=

Encuentre el adjunto de la array A calculando los cofactores de cada elemento y luego obteniendo la transpuesta de la array del cofactor.

adj A = 

Encuentre el valor del determinante de la array.

|A| = 1(1–16) – 2(2–12) + 3(8–3)

= 20

Entonces, la inversa de la array es,

A ^–1 = 

= 

Pregunta 5. Encuentra la inversa de la array A=  usando la fórmula.

Solución:

Tenemos,

A=

Encuentre el adjunto de la array A calculando los cofactores de cada elemento y luego obteniendo la transpuesta de la array del cofactor.

adj A =

Encuentre el valor del determinante de la array.

|A| = 2(0–3) – 3(0–3) + 4(1–2)

= –1

Entonces, la inversa de la array es,

A ^–1 = 

= 

Pregunta 6. Encuentra la inversa de la array A=  usando la fórmula.

Solución:

Tenemos,

A=

Encuentre el adjunto de la array A calculando los cofactores de cada elemento y luego obteniendo la transpuesta de la array del cofactor.

adj A = 

Encuentre el valor del determinante de la array.

|A| = 3(63–81) – 5(45–72) + 7(45–56)

= 4

Entonces, la inversa de la array es,

A ^–1 = 

=