Los números racionales son los números que se pueden expresar como la razón de dos números enteros. Incluye todos los números enteros y se puede expresar en términos de fracciones o decimales. Se denota por ‘Q’. Cuando se divide un número racional, la salida está en forma decimal, que puede ser final o repetitiva. 3, 4, 5, etc. son algunos ejemplos de números racionales, ya que se pueden expresar en forma de fracción como 3/1, 4/1 y 5/1.
Los números irracionales son números que no se pueden expresar en fracciones o proporciones de números enteros. Se puede escribir en decimales y tener un sinfín de dígitos que no se repiten después del punto decimal. Se denota por ‘P’.
Raíz cuadrada
El número en el que la multiplicación de un número por sí mismo da el número original se denomina raíz cuadrada. La raíz cuadrada de un número es un valor que se puede escribir como x = √y. Significa que ‘x’ es igual a la raíz cuadrada de y, donde ‘x’ es cualquier número natural. También podemos expresarlo como x 2 = y.
Por lo tanto, la raíz cuadrada es un valor que, cuando se multiplica por sí mismo, da el número original, es decir, y = x × x. Ejemplo: 5 × 5 = 25, y la raíz cuadrada de 25 es 5. Por ejemplo,
- ¿Encontrar la raíz cuadrada de 16?
Solución:
Dado: √16
= √(4 × 4)
= 4, por lo que 4 es la raíz cuadrada de 16.
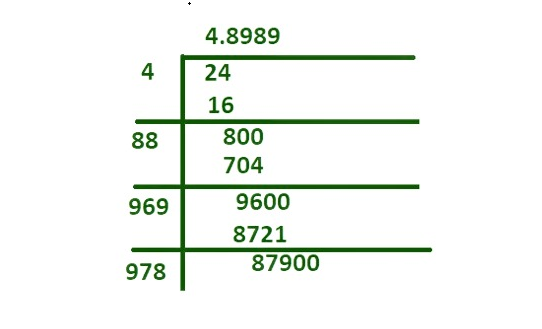
- ¿Encontrar la raíz cuadrada de 24?
Solución:
Aquí, la raíz cuadrada de 24 es irracional como 4.898979… Por lo tanto, no termina ni se repite.
¿La raíz cuadrada de 22 es un número racional?
Responder:
Los números racionales son los números que se pueden expresar como la razón de dos números enteros. Incluye todos los números enteros y se puede expresar en términos de fracciones o decimales. Se denota por ‘Q’.
Ejemplo: -4 , -6 , -14 , 0 , 1 , 2 , 5 etc.
Los números racionales tienen la forma p/q, donde p y q son números enteros y q ≠ 0. Debido a la estructura subyacente de los números, la forma p/q, a la mayoría de las personas les resulta difícil distinguir entre fracciones y números racionales.
Cuando se divide un número racional, la salida está en forma decimal, que puede ser final o repetitiva. 3, 4, 5, etc. son algunos ejemplos de números racionales, ya que se pueden expresar en forma de fracción como 3/1, 4/1 y 5/1.
Un número racional es una especie de número real que tiene la forma p/q donde q≠0. Cuando se divide un número racional, el resultado es un número decimal, que puede ser un decimal terminal o periódico.
Por lo tanto la raíz cuadrada de 22 es √22 = 4.690415….
Aquí, la respuesta a la pregunta anterior es que la raíz cuadrada de 22 no es un número racional, ya que no termina o no se repite después del decimal …
Problemas similares
Pregunta 1: Determine si 4.6904…. es un numero racional?
Responder:
Aquí, el número dado, 4.6904…. no tiene dígitos recurrentes. Por lo tanto, 4.6904…. no es un número racional.
Pregunta 2: ¿La raíz cuadrada de 6 es un número racional?
Responder:
Aquí, el número dado, √6 no se puede expresar en forma de p/q. Alternativamente, 6 no es un número primo sino un número racional. √6 es igual a 2.449489… lo que da el resultado de un dígito no recurrente y no terminado después del decimal, y no se puede expresar como fracción..,
Entonces √6 no es un número racional.
Pregunta 3: Determina si -7 es un número racional o un número irracional.
Responder:
Un número racional es una especie de número real que tiene la forma p/q donde q≠0. Cuando se divide un número racional, el resultado es un número decimal, que puede ser un decimal terminal o periódico.
Aquí, el número dado -8 es un número racional.
Pregunta 4: ¿Es √2 un número racional?
Responder:
Un número racional es una especie de número real que tiene la forma p/q donde q≠0. Cuando se divide un número racional, el resultado es un número decimal, que puede ser un decimal terminal o periódico. Aquí, el número dado, √2 no se puede expresar en forma de p/q. Alternativamente, 2 es un número primo o un número racional.
Aquí, el número dado √2 es igual a 1,4121, lo que da el resultado de un decimal que no termina ni se repite, y no se puede expresar como una fracción…
Entonces √2 es el número irracional.
Pregunta 5: ¿La raíz cuadrada de 12 es un número racional o irracional?
Responder:
Aquí, el número dado, √12 no se puede expresar en forma de p/q. Alternativamente, 12 no es un número primo sino un número racional.
Aquí, el número dado √12 es igual a 3.4641016… lo que da el resultado de un dígito no recurrente y no terminado después del decimal, y no puede expresarse como una fracción… Entonces √12 es un número irracional.
Pregunta 6: ¿√17 es un número racional o un número irracional?
Responder:
Aquí, el número dado, √17 no se puede expresar en forma de p/q. Alternativamente, 17 es un número primo. Esto significa que el número 7 no tiene par y no es divisible por 2. La raíz cuadrada de 17 es 4.1231056.. que no termina ni se repite después del decimal. Por lo tanto, √17 es un número irracional.
Pregunta 7: ¿√100 es un número racional o un número irracional?
Responder:
Aquí, el número dado, √100 = 10 o 10 2 = 10 × 10 = 100. La raíz cuadrada de 100 es 10, se puede expresar en forma de p/q y es el dígito final. Por lo tanto, √100 es un número racional.
Publicación traducida automáticamente
Artículo escrito por ManasChhabra2 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA