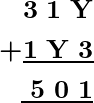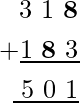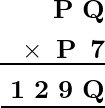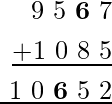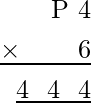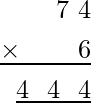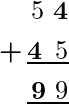Un número multiplicado por 2 da 60. ¿Cuál es ese número? El número es 30. Ese número no se conoce; asuma ese número como una variable y qué valor se asignará a esa variable para obtener el resultado de 60. La variable se define como una cantidad desconocida. No tiene un valor definido y sigue cambiando. Es un tipo de resolución de acertijos en el que se necesitaba determinar un valor para una letra específica. El valor de una letra tiene que tener sólo un dígito. Si hay varias letras en un rompecabezas, no se pueden asignar los mismos valores a varias letras. El valor de una letra no puede ser cero si la letra está en la posición inicial.
Letra para dígitos
Los problemas basados en este tema son algunos acertijos en los que las letras ocupan el lugar de los dígitos en una suma aritmética y la cuestión es averiguar qué letra representa qué dígito. Este tipo de pregunta desconcertante parece como descifrar un código usando operaciones aritméticas.
En este tipo de acertijos, la letra representa los dígitos, y uno necesita descifrar el código recordando algunas cosas en mente como:
- Cada dígito en la operación aritmética representa una sola letra y viceversa.
- Cualquier número utilizado en esto, no puede tener el primer dígito como cero, por ejemplo, 25 no debe ser 025 o 0025.
- Y cada rompecabezas debe tener una sola solución o código.
Rompecabezas con suma
Considere el siguiente ejemplo para un rompecabezas con suma que se da a continuación:
Ejemplo: Encuentra el valor de la incógnita Y en la siguiente suma:
Solución:
Se sabe que para la suma dada solo hay una letra Y cuyo valor se necesita determinar.
Considere la adición de la primera columna, es decir, de Y + 3 que da 1 en lugar de uno. Esto implica que Y puede ser 8 porque 8 + 3 = 11, es decir, 1 en el lugar de uno.
Si esto es así, entonces la adición dada debe escribirse como:
Por lo tanto, el valor de la incógnita Y es 8.
Rompecabezas con multiplicación
Considere el siguiente ejemplo para un rompecabezas con multiplicación a continuación:
Ejemplo: Determinar los valores de las incógnitas P y Q en la siguiente multiplicación.
Solución:
Considere la multiplicación de la primera columna, es decir, Q × 7, que de nuevo da Q en lugar de uno. Esto implica que Q puede ser 0 o 5 porque solo 0 × 7 = 0 y 5 × 7 = 25.
Ahora bien, para determinar el valor de P se presentan los siguientes casos:
Cuando P = 1 y Q = 0 entonces AB × A 7 = 1 0 × 1 7 = 170,
Cuando P = 1 y Q = 5 entonces AB × A 7 = 1 5 × 1 7 = 255,
Cuando P = 2 y Q = 0 entonces AB × A 7 = 2 0 × 2 7 = 540,
Cuando P = 2 y Q = 5 entonces AB × A 7 = 2 5 × 2 7 = 675,
Cuando P = 3 y Q = 0 entonces AB × A 7 = 3 0 × 3 7 = 1110 y
Cuando P = 3 y Q = 5 entonces AB × A 7 = 3 0 × 3 7 = 1295.
Por lo tanto, los valores requeridos de la incógnita son: P = 3 y Q = 5.
Problemas de muestra
Los siguientes son algunos problemas basados en los temas anteriores:
Problema 1: Encuentra el valor de las incógnitas C y D:
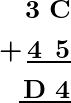
Solución:
Considere la adición de la primera columna, es decir, de C+ 5 que da 4 en lugar de uno. Esto implica que C puede ser 9 porque 9 + 5 = 14, es decir, 1 en el lugar de uno.
Si esto es así, entonces la adición dada debe escribirse como:
Por lo tanto, el valor de las incógnitas C = 9 y D = 8.
Problema 2: ¿Qué valor de Z se sustituye en la siguiente adición para que sea verdadero?
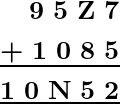
Solución:
En primer lugar, considere la suma de la primera columna, es decir, 7 + 5 = 12, esto implica que la suma en la segunda columna es: 1 + Z + 8 para dar 5 en el lugar de uno. Para este caso la Z debe ser 6.
Si esto es así, entonces la adición dada debe escribirse como:
Por lo tanto, el valor de Z es igual a 6.
Problema 3: ¿Qué valor de P y Q sustituyeron en el siguiente problema de multiplicación para que sea verdadero?
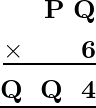
Solución:
Para el caso dado, el producto de Q y 6 debe ser igual a un dígito, es decir, Q.
Ahora,
1 × 6 = 6,
2 × 6 = 12,
3 × 6 = 18,
4 × 6 = 24
Así, uno de los dígitos multiplicados y el dígito de las unidades del producto obtenido es el mismo.
Entonces, la multiplicación dada se convierte en:
Ahora, el valor de P se obtiene como:
Al poner Q = 4, el dígito de las unidades debe obtenerse como 4 y los dos valores restantes de Q deben ser 44, lo que puede ser posible cuando se multiplica 7 con 6 para dar 44. Por lo tanto, la multiplicación dada se convierte en:
Por lo tanto, el valor de P y Q son 7 y 4.
Problema 4: ¿Qué valor de X e Y se sustituyeron en el siguiente problema de suma para que sea verdadero?
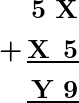
Solución:
Considere la primera columna de la suma, es decir, la suma de X y 5 da 9 en el lugar de uno, esto puede ser posible cuando se suma 4 a 5.
Por lo tanto, el problema de suma dado se convierte en:
Por lo tanto, el valor de X e Y son 4 y 9.
Problema 5: ¿Cuál es el valor de A – B cuando A 3 + 8 B = 150.
Solución:
Considere primero la suma de los dígitos del lugar de uno, es decir, la suma de 3 y B es tal que el dígito del lugar de uno es 0.
Esto es posible cuando B es 7, es decir, 3 + 7 = 10. Entonces, la suma dada se convierte en: 6 3 + 8 7 = 150.
Esto implica que A = 6 y B = 7.
Así, A – B = 6 – 7 = -1.
Publicación traducida automáticamente
Artículo escrito por mayurigrover y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA