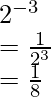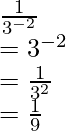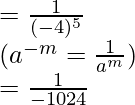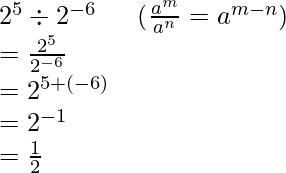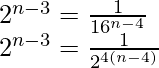Leyes de exponentes para números reales

A veces nos encontramos con números muy grandes como la masa de la tierra. La masa de la tierra es 5,970,000,000,000, 000, 000, 000, 000 kg. No hay problema en escribir la masa de la tierra como esta, pero a veces durante los cálculos que involucran tales objetos. Se vuelve engorroso y difícil de usar. Por eso se inventaron los exponentes. Para facilitar el manejo de números muy grandes o muy pequeños. Este número se puede escribir como 5,97 × 10 ²⁴ kg. Se lee 5,97 por 10 elevado a la potencia 24. Estudiemos algunas leyes con respecto a estos números exponentes.

Leyes de los Exponentes

Estas leyes nos ayudan a simplificar nuestros cálculos.

ley del producto

La ley del producto establece que si la base de dos números es la misma, sus exponentes se pueden sumar directamente.

un ^metro × un norte = un ^metro+ⁿ

Para verificar esta propiedad, vea cuántas veces se multiplica «a» en total. Se multiplica “m + n” veces. Así, la propiedad.

Ejemplo: a ² a ³ = (aa)(aaa) = a ⁵

ley del cociente

De acuerdo con esta ley, si los dos números en el numerador y el denominador son iguales, sus exponentes se pueden ordenar de tal manera que el exponente en el denominador se reste por el exponente en el numerador.

$\frac{a^m}{a^n} = a^{m-n}$

Esto también se puede verificar similar al anterior, solo ver la cantidad de veces que se multiplica a y luego reducir ese número por la cantidad de veces que se divide.

Ejemplo: $\frac{x^4}{x^2} =\frac{xxxx}{xx} = x^{4-2} = x^2$

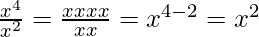
Ley de potencia

Según la ley de potencias, si un exponente es una potencia de otro exponente, simplemente podemos multiplicar los exponentes.

(un ^m ) ⁿ = un ^mn

Primero, multiplica «a» m veces y luego haz esta operación n veces.

Ejemplo: (x ³ ) ² = (xxx) ² = (xxx)(xxx) = x ⁶ = x ^{(3 × 2)}

Ley del poder del producto

De acuerdo con la ley de la potencia del producto, si dos números reales dicen, a y b aquí se multiplican y se elevan a la potencia m, podemos distribuir el exponente tanto a a como a b por separado.

un ^metro xb metro ⁼ (ab) ^metro

Esta propiedad es solo un reordenamiento de todas estas variables.

Ejemplo: a ³ × b ³ = (aaa) (bbb) = (ab)(ab)(ab) = (ab) ³

Ley de la potencia del cociente

De acuerdo con la ley de la potencia del cociente, si dos números reales están en el numerador y el denominador y se elevan a la potencia n, la potencia se puede distribuir por separado a ambos números.

$(\frac{x}{y})^n = \frac{x^n}{y^n}$

Esto también se puede verificar mediante un simple reordenamiento de las variables.

Ejemplo: $\frac{x^3}{y^3} = \frac{xxx}{yyy} = \frac{x}{y}\frac{x}{y}\frac{x}{y} = (\frac{x}{y})^{3}$

Regla de potencia cero

Siempre que x no sea igual a cero, elevarlo a la potencia de cero debería dar como resultado 1.

un ⁰ = 1, un ≠ 1.

Pongamos un ejemplo para que esto sea más evidente,

1 = $1 = \frac{x^a}{x^a} = x^{a - a} = x^0$

Nota:

La expresión 0 ⁰ se considera indeterminada. ¿Por qué? Porque hay dos respuestas.

Sabemos, x ⁰ = 1, Entonces, 0 ⁰ = 1.

También sabemos, 0 ^x = 0. Entonces, 0 ⁰ = 0.

Estas son dos respuestas contradictorias, por lo que consideramos que 0 ⁰ es indeterminado.

exponente de exponente

A veces, en escenarios más complejos, se dan exponentes sobre exponentes. Vamos a ver cómo acercarnos a ellos,

$5^{2^{4}}$

Empezaremos a resolver desde arriba,

$5^{2^{4}} \\ = 5^{16}$

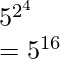
Veamos algunos ejemplos y preguntas donde estas propiedades son aplicables.

Problemas de muestra

Pregunta 1: Encuentra el valor de 2 ^-3

Responder:

$2^{-3}\\ = \frac{1}{2^3}\\ = \frac{1}{8}$

Pregunta 2: $\frac{1}{3^{-2}}$

Responder:

$\frac{1}{3^{-2}} \\ = 3^{-2} \\ = \frac{1}{3^2} \\= \frac{1}{9}$

Pregunta 3: simplifica el uso de las propiedades anteriores:

(-4) ⁵ × (-4) ^-10

Responder:

(-4) ⁵ × (-4) ^-10

= -4 ^(5-10) (un ^metro × un norte = un ^metro+ⁿ )

= (-4) ^-5

$\\ = \frac{1}{(-4)^5}\\ \hspace{0.6cm} (a^{-m} = \frac{1}{a^m}) \\ = \frac{1}{-1024}$

Pregunta 4: simplifica el uso de las propiedades anteriores:

$2^5 \div 2^{-6}$

Responder:

$2^5 \div 2^{-6} \hspace{0.6cm} (\frac{a^m}{a^n} = a^{m-n})\\ = \frac{2^5}{2^{-6}} \\ = 2^{5 + (-6)} \\ = 2^{-1} \\ = \frac{1}{2}$

Pregunta 5: simplifica, $(x^3 \div x^{\frac{1}{2}}) \times (x^{\frac{3}{2}} \div x^{0}) \times x^7$

Responder:

$(x^3 \div x^{\frac{1}{2}}) \times (x^{\frac{3}{2}} \div x^{0}) \times x^7 \\ = \frac{x^3}{x^{\frac{1}{2}}} \times \frac{x^{\frac{3}{2}}}{x^0} \times x^7 \\ = x^{3 - \frac{1}{2}} \times x^{\frac{3}{2} - 0} \times x^{7} \\ = x^{\frac{5}{2}} \times x^{\frac{3}{2}} \times x^{7} \\ = x^{\frac{5}{2} + \frac{3}{2} + 7} \\ = x^{\frac{5 + 3+ 14}{2}} \\ = x^{\frac{22}{2}}\\ = x^{11}$

Pregunta 6: ¿Cuál es la quinta raíz de 5 ¹⁵ .

Responder:

Sabemos que la enésima parte de un número “a” está representada por $a^{\frac{1}{n}}$

Por lo tanto, 5 de 5 ¹⁵ estará dado por,

$5^{\frac{15}{5}}$

= 5 ³

= 125

Pregunta 7: Encuentra el valor de n

$2^{n-3} = \frac{1}{16^{n-4}}$

Responder:

$2^{n-3} = \frac{1}{16^{n-4}} \\ 2^{n-3} = \frac{1}{2^{4(n-4)}}$

2 ^n-3 × 2 ^{4n – 16} = 1

2n- 3 ^{+ 4n-16} = 2 ⁰

Comparando ambos lados

n-3 + 4n-16 = 0

5n -19 = 0

$\\ n = \frac{19}{5}$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Leyes de los Exponentes

ley del producto

ley del cociente

Ley de potencia

Ley del poder del producto

Ley de la potencia del cociente

Regla de potencia cero

exponente de exponente

Problemas de muestra

Deja una respuesta Cancelar la respuesta