Hay seis funciones trigonométricas como sabemos. El límite de cada función que tiende a un punto se puede calcular de acuerdo a la continuidad de la función considerando su dominio y rango. Esto lo podemos observar en la gráfica de cada función que el límite de cada función en un mismo punto es diferente.
función seno
La función f(x) = sin(x) es una función continua en todo su dominio, cuyo dominio consta de todos los números reales. El rango de esta función es [-1, 1] como se puede ver en el siguiente gráfico:
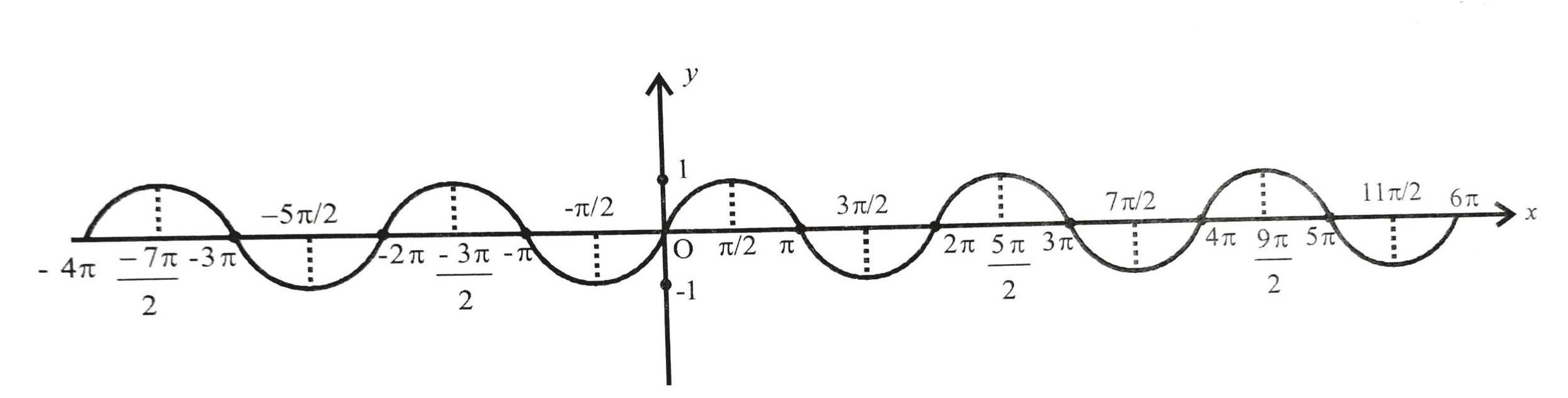
Entonces, si el límite de la función seno se calcula en cualquier número real dado, siempre está definido y se encuentra entre [-1, 1].
f(x) = sen(x)
lím x→a f(x) = lím x→a sen(x)
= sin(a), donde a es un número real
Ejemplo 1: Encuentra lim x→π/2 sin(x)
Solución:
Como sabemos, sin(x) se define en π/2
Por lo tanto,
lím x→π/2 sin(x) = sin(π/2) = 1
Ejemplo 2: Encuentra lim x→π sin(x)
Solución:
Como sabemos, sin(x) está definido en π
Por lo tanto,
lím x→π in(x) = sin(π) = 0
Función coseno
La función f(x) = cos(x) es una función continua en todo su dominio, cuyo dominio consta de todos los números reales.
El rango de esta función es [-1, 1] como se puede ver en el siguiente gráfico:

Entonces, si el límite de la función coseno se calcula en cualquier número real dado, siempre está definido y se encuentra entre [-1, 1].
f(x) = cos(x)
lím x→a f(x) = lím x→a cos(x)
= cos(a), donde a es un número real
Ejemplo 1: encontrar lím x→π/2 cos(x)
Solución:
Como sabemos cos(x) es continuo y definido en π/2
Por lo tanto,
lím x→π/2 cos(x) = cos(π/2) = 0
Ejemplo 2: Encuentra lim x→π cos(x)
Solución:
Como sabemos cos(x) es continuo y definido en π
Por lo tanto,
lím x→π cos(x) = cos(π) = -1
Función tangente
La función f(x) = tan(x) está definida en todos los números reales excepto los valores donde cos(x) es igual a 0, es decir, los valores π/2 + πn para todos los números enteros n. Por lo tanto, su dominio son todos los números reales excepto π/2 + πn, n € Z.
El rango de esta función es (-∞, +c).

Entonces, si el límite de la función tangente se calcula en su dominio, siempre está definido y se encuentra entre (-∞, +∞).
f(x) = tan(x)
lím x→a f(x) = lím x→a tan(x)
= tan(a), donde a pertenece al real no. excepto π/2 + πn, n € Z
Ejemplo 1: Encuentra lim x→π/2 tan(x)
Solución:
Como podemos ver en el gráfico, tan(x) tiende a +∞ cuando x→-π/2 y a -∞ cuando x→+π/2
Entonces, los límites derecho e izquierdo de esta función en π/2 no son iguales
Por lo tanto,
lím x→π/2 tan(x) = No definido
Ejemplo 2: Encuentra lim x→π tan(x)
Solución:
Como sabemos tan(x) es continua y definida en π
Por lo tanto,
lím x→π tan(x) = tan(π) = 0
Función Cosec
La función f(x) = cosec(x) se define en todos los números reales excepto los valores donde sin(x) es igual a 0, es decir, los valores πn para todos los números enteros n. Por lo tanto, su dominio son todos los números reales excepto πn, n € Z.
El rango de esta función es (-∞,-1] U [1,+∞).
Entonces, si el límite de la función coseno se calcula en su dominio, siempre está definido y se encuentra entre su rango.
f(x) = cosec(x)
lím x→a f(x) = lím x→a cosec(x)
= cosec(a), donde a pertenece al número real. excepto para πn , n € Z
Ejemplo 1: Encuentra lim x→ π cosec(x)
Solución:
Como sabemos sen(x) es 0 cuando x→ π
Entonces, 1/sen(x) es decir, cosec(x) en π no se puede definir
Por lo tanto,
lím x→ π cosec(x) = No definido
Ejemplo 2: Encuentra lim x→ π /2 cosec(x)
Solución:
Como sabemos tan(x) es continua y definida en π /2
Por lo tanto,
lím x→ π /2 cosec(x) = cosec( π /2) = 1
función secante
La función f(x) = sec(x) está definida en todos los números reales excepto los valores donde cos(x) es igual a 0, es decir, los valores π/2 + πn para todos los números enteros n. Por lo tanto, su dominio son todos los números reales excepto π/2 + πn, n € Z.
El rango de esta función es (-∞, -1] U [1, +∞)
Entonces, si el límite de la función sec se calcula en su dominio, siempre se define y se encuentra entre su rango.
f(x) = segundo(x)
lím x→a f(x) = lím x→a sec(x)
= sec(a), donde a pertenece al número real. excepto π/2 + πn, n € Z
Ejemplo 1: Encontrar lím x→ π /2 seg(x)
Solución:
Como sabemos cos(x) es 0 cuando x→ π /2
Entonces, 1/cos(x) es decir, sec(x) en π /2 no se puede definir
Por lo tanto,
lím x→ π /2 seg(x) = No definido
Ejemplo 2: Encuentra lim x→ π sec(x)
Solución:
Como sabemos tan(x) es continua y definida en π
Por lo tanto,
lím x→ π cosec(x) = sec( π ) = -1
Función de cuna
La función f(x) = cot(x) se define en todos los números reales excepto los valores donde tan(x) es igual a 0, es decir, los valores πn para todos los números enteros n. Por lo tanto, su dominio son todos los números reales excepto πn, n € Z.
El rango de esta función es (-∞, +∞)
Entonces, si el límite de la función cot se calcula en su dominio, siempre está definido y se encuentra entre su rango.
f(x) = cuna(x)
lím x→a f(x) = lím x→a cot(x)
= cot(a), donde a pertenece al real no. excepto para πn, n € Z
Ejemplo 1: Encuentra lim x→π cot(x)
Solución:
Como sabemos, tan(x) es 0 cuando x→π
Entonces, 1/tan(x) es decir, cot(x) en π no se puede definir
Por lo tanto,
limx→π cot(x) = No definido
Ejemplo 2: Encuentra lim x→π/2 cot(x)
Solución:
Como sabemos cot(x) es continua y definida en π/2
Por lo tanto,
límite x→π/2 cuna(x) = cuna(π/2) = 0
Teorema del sándwich (Teorema del apretón)
El teorema se usa para calcular el límite de aquellas funciones cuyo límite no se puede calcular fácilmente como (sin x/x en x = 0).
La función g(x) está comprimida o intercalada entre dos funciones h(x) y g(x) de tal manera que f (x) ≤ g(x) ≤ h(x ) .
El gráfico bajo tal condición se puede ver a continuación:
Podemos decir que h(x) es el límite superior de g(x) y f(x) es su límite inferior en un punto a como se puede observar en el gráfico anterior:
si,
lím x→a h(x) = L y lím x→a f(x) = L,
donde a es el punto en el que se calcula el límite y L es el valor del límite
Después,
lím x→a g(x) = L
Ejemplo 1: Dado: g(x) = x2sin(1/x), Hallar: lim x→0 g(x)
Solución:
Sabemos,
-1≤ sin(1/x) ≤ 1 bajo su dominio
Multiplicando por x2,
-x2 ≤ x2sen(1/x) ≤ x2
Entonces sea f(x) = -x2 y h(x) = x2
f(x) ≤ g(x) ≤ h(x)
Usando el teorema del sándwich,
Como lím x→a h(x) = lím x→a f(x) = L
Por lo tanto,
lím x→a g(x) = L
lím x→0 f(x) = lím x→0 -x2 = 0 y
límite x→0 h(x) = límite x→0 x2 = 0
Por lo tanto,
límite x→0 g(x) = 0
Ejemplo 2: Dado: g(x) = cos(x)/x, Encuentra: lim x→∞ g(x)
Solución:
Sabemos,
-1≤ cos(x)≤ 1 bajo su dominio
Dividiendo por x,
-1/x ≤ cos(x)/x ≤ 1/x
Entonces sea f(x) = -1/x y h(x) = 1/x
f(x) ≤ g(x) ≤ h(x)
Usando el teorema del sándwich,
Como lím x→a h(x) = lím x→ af(x) = L
Por lo tanto,
lím x→a g(x) = L
lím x→∞ f(x) = lím x→∞ -1/x = 0 y
límite x→∞ h(x) = límite x→∞ 1/x = 0
Por lo tanto,
límite x→∞ g(x) = 0
Publicación traducida automáticamente
Artículo escrito por shubhigupta22 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
