Los límites son componentes básicos del cálculo. Son los valores que parece tomar una función mientras llegamos a un punto determinado. Ayudan a calcular la tasa de cambio de las funciones. El concepto de derivados ha sido definido con límites. También nos ayudan a definir los conceptos de continuidad y diferenciabilidad. Por lo tanto, se vuelve esencial comprender su intuición y los diferentes métodos para calcular los límites de las diferentes categorías de funciones.
Límites
Hablando geométricamente, el límite de una función en un punto particular se puede estimar fácilmente a través de su gráfico. Por ejemplo, en el gráfico que se muestra a continuación, en x = 3. La función parece tomar el valor de 1. En este caso, no importa desde qué lado nos acerquemos: el lado izquierdo y el lado derecho. .

Para la función f(x), el límite en x = a se denota por,
![]()
Límites mediante sustitución directa
La regla de sustitución para calcular límites es un método para encontrar límites, simplemente sustituyendo el valor de x con el punto en el que queremos calcular el límite. Considere una función f(x), el objetivo es encontrar el límite de la función en x = a. En este método, x simplemente se sustituye por “a” en la expresión de la función f(x).
![]()
Veamos este método a través de un ejemplo,
Considerando f(x) = x 2 ,
![]()
⇒![]()
⇒![]()
⇒![]()
A menudo es posible calcular los límites de la función con esta regla, para decirlo formalmente.
Si f(x) es una expresión construida a partir de polinomios, raíces, valores absolutos, funciones exponenciales, logaritmos, trigonométricas y/o funciones trigonométricas inversas usando la composición de funciones y operaciones como x, +, -, / entonces para cualquier a para el que se define f(a),
Límites indefinidos por sustitución directa
Hay ciertos límites que no pueden ser calculados por este método. Por ejemplo, considere una función f(x) = , calcule el límite para esta función en x = 1. ![]()
![]()
⇒![]()
⇒![]()
⇒![]()
Este límite no está definido. En tales casos, el método de sustitución directa.
Límites de la función trigonométrica
A veces se puede usar la sustitución directa para calcular los límites de funciones que involucran funciones trigonométricas. Por ejemplo, digamos que tenemos una función f(x) y queremos calcular los límites para esa función en x = 0. Veamos esto con un ejemplo.
Ejemplo: Calcular el ![]()
f(x) = sen(x) + sen(x)cos(x)
Solución:
⇒
⇒
⇒
⇒0 × (1 + 1)
⇒ 0
Límites de la función por partes
Cuando se trabaja con funciones definidas por partes, la regla de sustitución generalmente no funciona en los lugares donde cambia la definición de la función. Se utiliza de forma un poco modificada para esas funciones. Resolvamos un problema de muestra para comprender mejor esto,
Ejemplo: Calcular el valor de ![]() .
.

Solución:
En x = 1, la definición de la función está cambiando. Por lo tanto, no se recomienda aplicar directamente la regla. En tales funciones, uno debe buscar el límite de ambos lados.
Límite del lado izquierdo
⇒
⇒1
Límite del lado derecho
⇒
⇒0
En este caso, los límites de ambos lados son diferentes.
Veamos algunos problemas sobre estos conceptos
Problemas de muestra
Pregunta 1: Calcular el ![]()
f(x) = x2 + x + 1
Solución:
⇒
⇒
⇒ 1
Pregunta 2: Calcular el ![]()
f(x) = ![]()
Solución:
⇒ \
⇒
⇒
Pregunta 3: Calcula el valor de ![]() .
.
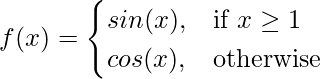
Solución:
En x = 1, la definición de la función está cambiando. Por lo tanto, no se recomienda aplicar directamente la regla. En tales funciones, uno debe buscar el límite de ambos lados.
Límite del lado izquierdo
⇒
Límite del lado derecho
⇒
En este caso, los límites de ambos lados son diferentes.
Pregunta 4: Calcular el ![]()
f(x) = ![]()
Solución:
⇒ \
⇒
⇒
⇒ mi + 2
Pregunta 5: Calcular el ![]()
f(x) = ![]()
Solución:
⇒ \
⇒
⇒
⇒ e sen(1) + 2
Pregunta 6: Calcular el ![]() uso de la regla de sustitución.
uso de la regla de sustitución.
f(x) = ![]()
Solución:
⇒ \
⇒
Esta es la forma 0/0, por lo que el límite no está definido. La regla de sustitución no se puede utilizar aquí.
Pregunta 7: Calcula el valor de ![]() .
.
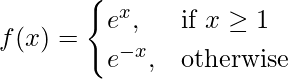
Solución:
En x = 1, la definición de la función está cambiando. Por lo tanto, no se recomienda aplicar directamente la regla. En tales funciones, uno debe buscar el límite de ambos lados.
Límite del lado izquierdo
⇒
Límite del lado derecho
⇒
En este caso también, los límites de ambos lados son diferentes.
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA