Logaritmo discreto (Encuentre un entero k tal que a^k sea congruente módulo b)

Posted on by Rudeus Greyrat

Dados tres enteros a, b y m. Encuentre un entero k tal que  a^k \equiv b \pmod m donde a y m sean primos relativos. Si no es posible que ningún k satisfaga esta relación, imprima -1.
Ejemplos: 
 

Input: 2 3 5
Output: 3
Explanation:
a = 2, b = 3, m = 5
The value which satisfies the above equation
is 3, because 
=> 23 = 2 * 2 * 2 = 8
=> 23 (mod 5) = 8 (mod 5) 
=> 3
which is equal to b i.e., 3.

Input: 3 7 11
Output: -1

Un enfoque ingenuo es ejecutar un ciclo de 0 a m para cubrir todos los valores posibles de k y verificar qué valor de k satisface la relación anterior. Si se agotan todos los valores de k, imprima -1. La complejidad de tiempo de este enfoque es O(m) 
Un enfoque eficiente es usar un algoritmo de paso pequeño, paso gigante usando el truco de encontrarse en el medio .
 

Algoritmo de pasos de gigante paso de bebé

Dado un grupo cíclico G de orden ‘m’, un generador ‘a’ del grupo, y un elemento de grupo ‘b’, el problema es encontrar un entero ‘k’ tal que  a^k \equiv b \pmod m
Entonces lo que vamos a hacer (según Meet in the middle trick) es dividir el problema en dos partes de  cada una y resolverlas individualmente y luego encontrar la colisión. 
 

Now according to the baby-step giant-step 
algorithm, we can write 'k' as 
k=i\cdot n - j with n = \left\lceil \sqrt{m} \right\rceil 
and 0 \leq i < n and 0\leq j<n.
Therefore, we have:
\implies a^{i\cdot n - j} = b \pmod m
\implies a^{i\cdot n} = a^{j}\cdot b \pmod m
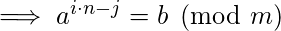
Therefore in order to solve, we precompute 
a^{i\cdot n} for different values of 'i'. 
Then fix 'b' and tries values of 'j' 
In RHS of the congruence relation above. It 
tests to see if congruence is satisfied for 
any value of 'j', using precomputed 
values of LHS.

Veamos cómo usar el algoritmo anterior para nuestra pregunta:
primero que nada, tenemos que escribir  k = i\cdot n - j , donde  n = \left\lceil \sqrt{m} \right\rceil Obviamente, cualquier valor de k en el intervalo [0, m) se puede representar de esta forma, donde  i \in [1, n) y  j \in [0, n)
Reemplace la ‘k’ en por encima de la igualdad, obtenemos: – 
\implies a^k = b \pmod m
\implies a^{i\cdot n - j} = b \pmod m
\implies a^{i\cdot n} = a^j\cdot b \pmod m
 

  1. El término izquierda y derecha sólo puede tomar n valores distintos como 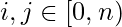 i, j \in [0, n) . Por lo tanto, necesitamos generar todos estos términos para la parte izquierda o derecha de la igualdad y almacenarlos en una array o estructura de datos como map/unordered_map en C/C++ o Hashmap en Java.
  2. Supongamos que hemos almacenado todos los valores de LHS. Ahora itere sobre todos los términos posibles en el RHS para diferentes valores de j y verifique qué valor satisface la igualdad del LHS.
  3. Si ningún valor satisface el paso anterior para ningún candidato de j, imprima -1. 
     

C++

// C++ program to calculate discrete logarithm
#include<bits/stdc++.h>
using namespace std;
 
/* Iterative Function to calculate (x ^ y)%p in
   O(log y) */
int powmod(int x, int y, int p)
{
    int res = 1;  // Initialize result
 
    x = x % p;  // Update x if it is more than or
                // equal to p
 
    while (y > 0)
    {
        // If y is odd, multiply x with result
        if (y & 1)
            res = (res*x) % p;
 
        // y must be even now
        y = y>>1; // y = y/2
        x = (x*x) % p;
    }
    return res;
}
 
// Function to calculate k for given a, b, m
int discreteLogarithm(int a, int b, int m) {
 
    int n = (int) sqrt (m) + 1;
 
    unordered_map<int, int> value;
 
    // Store all values of a^(n*i) of LHS
    for (int i = n; i >= 1; --i)
        value[ powmod (a, i * n, m) ] = i;
 
    for (int j = 0; j < n; ++j)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        int cur = (powmod (a, j, m) * b) % m;
 
        // If collision occurs i.e., LHS = RHS
        if (value[cur])
        {
            int ans = value[cur] * n - j;
            // Check whether ans lies below m or not
            if (ans < m)
                return ans;
        }
    }
    return -1;
}
 
// Driver code
int main()
{
    int a = 2, b = 3, m = 5;
    cout << discreteLogarithm(a, b, m) << endl;
 
    a = 3, b = 7, m = 11;
    cout << discreteLogarithm(a, b, m);
}

Java

// Java program to calculate discrete logarithm
 
class GFG{
/* Iterative Function to calculate (x ^ y)%p in
O(log y) */
static int powmod(int x, int y, int p)
{
    int res = 1; // Initialize result
 
    x = x % p; // Update x if it is more than or
                // equal to p
 
    while (y > 0)
    {
        // If y is odd, multiply x with result
        if ((y & 1)>0)
            res = (res*x) % p;
 
        // y must be even now
        y = y>>1; // y = y/2
        x = (x*x) % p;
    }
    return res;
}
 
// Function to calculate k for given a, b, m
static int discreteLogarithm(int a, int b, int m) {
 
    int n = (int) (Math.sqrt (m) + 1);
 
    int[] value=new int[m];
 
    // Store all values of a^(n*i) of LHS
    for (int i = n; i >= 1; --i)
        value[ powmod (a, i * n, m) ] = i;
 
    for (int j = 0; j < n; ++j)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        int cur = (powmod (a, j, m) * b) % m;
 
        // If collision occurs i.e., LHS = RHS
        if (value[cur]>0)
        {
            int ans = value[cur] * n - j;
            // Check whether ans lies below m or not
            if (ans < m)
                return ans;
        }
    }
    return -1;
}
 
// Driver code
public static void main(String[] args)
{
    int a = 2, b = 3, m = 5;
    System.out.println(discreteLogarithm(a, b, m));
 
    a = 3;
    b = 7;
    m = 11;
    System.out.println(discreteLogarithm(a, b, m));
}
}
// This code is contributed by mits

Python3

# Python3 program to calculate
# discrete logarithm
import math;
 
# Iterative Function to calculate
# (x ^ y)%p in O(log y)
def powmod(x, y, p):
 
    res = 1; # Initialize result
 
    x = x % p; # Update x if it is more
               # than or equal to p
 
    while (y > 0):
         
        # If y is odd, multiply x with result
        if (y & 1):
            res = (res * x) % p;
 
        # y must be even now
        y = y >> 1; # y = y/2
        x = (x * x) % p;
    return res;
 
# Function to calculate k for given a, b, m
def discreteLogarithm(a, b, m):
    n = int(math.sqrt(m) + 1);
 
    value = [0] * m;
 
    # Store all values of a^(n*i) of LHS
    for i in range(n, 0, -1):
        value[ powmod (a, i * n, m) ] = i;
 
    for j in range(n):
         
        # Calculate (a ^ j) * b and check
        # for collision
        cur = (powmod (a, j, m) * b) % m;
 
        # If collision occurs i.e., LHS = RHS
        if (value[cur]):
            ans = value[cur] * n - j;
             
            # Check whether ans lies below m or not
            if (ans < m):
                return ans;
     
    return -1;
 
# Driver code
a = 2;
b = 3;
m = 5;
print(discreteLogarithm(a, b, m));
 
a = 3;
b = 7;
m = 11;
print(discreteLogarithm(a, b, m));
 
# This code is contributed by mits

C#

// C# program to calculate discrete logarithm
using System;
class GFG{
/* Iterative Function to calculate (x ^ y)%p in
O(log y) */
static int powmod(int x, int y, int p)
{
    int res = 1; // Initialize result
 
    x = x % p; // Update x if it is more than or
                // equal to p
 
    while (y > 0)
    {
        // If y is odd, multiply x with result
        if ((y & 1)>0)
            res = (res*x) % p;
 
        // y must be even now
        y = y>>1; // y = y/2
        x = (x*x) % p;
    }
    return res;
}
 
// Function to calculate k for given a, b, m
static int discreteLogarithm(int a, int b, int m) {
 
    int n = (int) (Math.Sqrt (m) + 1);
 
    int[] value=new int[m];
 
    // Store all values of a^(n*i) of LHS
    for (int i = n; i >= 1; --i)
        value[ powmod (a, i * n, m) ] = i;
 
    for (int j = 0; j < n; ++j)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        int cur = (powmod (a, j, m) * b) % m;
 
        // If collision occurs i.e., LHS = RHS
        if (value[cur]>0)
        {
            int ans = value[cur] * n - j;
            // Check whether ans lies below m or not
            if (ans < m)
                return ans;
        }
    }
    return -1;
}
 
// Driver code
static void Main()
{
    int a = 2, b = 3, m = 5;
    Console.WriteLine(discreteLogarithm(a, b, m));
 
    a = 3;
    b = 7;
    m = 11;
    Console.WriteLine(discreteLogarithm(a, b, m));
}
}
// This code is contributed by mits

PHP

<?php
// PHP program to calculate
// discrete logarithm
 
// Iterative Function to calculate
// (x ^ y)%p in O(log y)
function powmod($x, $y, $p)
{
    $res = 1; // Initialize result
 
    $x = $x % $p; // Update x if it is more
                  // than or equal to p
 
    while ($y > 0)
    {
        // If y is odd, multiply x with result
        if ($y & 1)
            $res = ($res * $x) % $p;
 
        // y must be even now
        $y = $y >> 1; // y = y/2
        $x = ($x * $x) % $p;
    }
    return $res;
}
 
// Function to calculate k for given a, b, m
function discreteLogarithm($a, $b, $m)
{
    $n = (int)sqrt($m) + 1;
 
    $value = array_fill(0, $m, NULL);
 
    // Store all values of a^(n*i) of LHS
    for ($i = $n; $i >= 1; --$i)
        $value[ powmod ($a, $i * $n, $m) ] = $i;
 
    for ($j = 0; $j < $n; ++$j)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        $cur = (powmod ($a, $j, $m) * $b) % $m;
 
        // If collision occurs i.e., LHS = RHS
        if ($value[$cur])
        {
            $ans = $value[$cur] * $n - $j;
             
            // Check whether ans lies below m or not
            if ($ans < $m)
                return $ans;
        }
    }
    return -1;
}
 
// Driver code
$a = 2;
$b = 3;
$m = 5;
echo discreteLogarithm($a, $b, $m), "\n";
 
$a = 3;
$b = 7;
$m = 11;
echo discreteLogarithm($a, $b, $m), "\n";
 
// This code is contributed by ajit.
?>

Javascript

<script>
 
    // Javascript program to calculate
    // discrete logarithm
     
    /* Iterative Function to
    calculate (x ^ y)%p in
    O(log y) */
    function powmod(x, y, p)
    {
        // Initialize result
        let res = 1;
 
        // Update x if it is more
        // than or
        // equal to p
        x = x % p;
                     
        while (y > 0)
        {
            // If y is odd, multiply x
            // with result
            if ((y & 1)>0)
                res = (res*x) % p;
 
            // y must be even now
            y = y>>1; // y = y/2
            x = (x*x) % p;
        }
        return res;
    }
 
    // Function to calculate
    // k for given a, b, m
    function discreteLogarithm(a, b, m) {
 
        let n = (parseInt(Math.sqrt(m), 10) + 1);
 
        let value = new Array(m);
        value.fill(0);
 
        // Store all values of a^(n*i) of LHS
        for (let i = n; i >= 1; --i)
            value[ powmod (a, i * n, m) ] = i;
 
        for (let j = 0; j < n; ++j)
        {
            // Calculate (a ^ j) * b and check
            // for collision
            let cur = (powmod (a, j, m) * b) % m;
 
            // If collision occurs
            // i.e., LHS = RHS
            if (value[cur]>0)
            {
                let ans = value[cur] * n - j;
                // Check whether ans lies
                // below m or not
                if (ans < m)
                    return ans;
            }
        }
        return -1;
    }
     
    let a = 2, b = 3, m = 5;
    document.write(
    discreteLogarithm(a, b, m) + "</br>"
    );
  
    a = 3;
    b = 7;
    m = 11;
    document.write(
    discreteLogarithm(a, b, m) + "</br>"
    );
 
</script>

Producción:  

3
-1

Complejidad temporal: O(sqrt(m)*log(b)) 
Espacio auxiliar: O(sqrt(m))
Una posible mejora es eliminar la exponenciación binaria o el factor log(b) en la segunda fase del algoritmo. Esto se puede hacer manteniendo una variable que se multiplique por ‘a’ cada vez que ‘an’. Veamos el programa para entender más.
 

C++

// C++ program to calculate discrete logarithm
#include<bits/stdc++.h>
using namespace std;
 
int discreteLogarithm(int a, int b, int m)
{
    int n = (int) sqrt (m) + 1;
 
    // Calculate a ^ n
    int an = 1;
    for (int i = 0; i<n; ++i)
        an = (an * a) % m;
 
    unordered_map<int, int> value;
 
    // Store all values of a^(n*i) of LHS
    for (int i = 1, cur = an; i<= n; ++i)
    {
        if (! value[ cur ])
            value[ cur ] = i;
        cur = (cur * an) % m;
    }
 
    for (int i = 0, cur = b; i<= n; ++i)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        if (value[cur])
        {
            int ans = value[cur] * n - i;
            if (ans < m)
                return ans;
        }
        cur = (cur * a) % m;
    }
    return -1;
}
 
// Driver code
int main()
{
    int a = 2, b = 3, m = 5;
    cout << discreteLogarithm(a, b, m) << endl;
 
    a = 3, b = 7, m = 11;
    cout << discreteLogarithm(a, b, m);
}

Java

// Java program to calculate discrete logarithm
 
class GFG
{
 
    static int discreteLogarithm(int a, int b, int m)
    {
        int n = (int) (Math.sqrt (m) + 1);
 
        // Calculate a ^ n
        int an = 1;
        for (int i = 0; i < n; ++i)
            an = (an * a) % m;
 
        int[] value=new int[m];
 
        // Store all values of a^(n*i) of LHS
        for (int i = 1, cur = an; i <= n; ++i)
        {
            if (value[ cur ] == 0)
                value[ cur ] = i;
            cur = (cur * an) % m;
        }
 
        for (int i = 0, cur = b; i <= n; ++i)
        {
            // Calculate (a ^ j) * b and check
            // for collision
            if (value[cur] > 0)
            {
                int ans = value[cur] * n - i;
                if (ans < m)
                    return ans;
            }
            cur = (cur * a) % m;
        }
        return -1;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int a = 2, b = 3, m = 5;
        System.out.println(discreteLogarithm(a, b, m));
        a = 3;
        b = 7;
        m = 11;
        System.out.println(discreteLogarithm(a, b, m));
    }
}
 
// This code is contributed by mits

Python3

# Python3 program to calculate
# discrete logarithm
import math;
 
def discreteLogarithm(a, b, m):
 
    n = int(math.sqrt (m) + 1);
 
    # Calculate a ^ n
    an = 1;
    for i in range(n):
        an = (an * a) % m;
 
    value = [0] * m;
 
    # Store all values of a^(n*i) of LHS
    cur = an;
    for i in range(1, n + 1):
        if (value[ cur ] == 0):
            value[ cur ] = i;
        cur = (cur * an) % m;
     
    cur = b;
    for i in range(n + 1):
         
        # Calculate (a ^ j) * b and check
        # for collision
        if (value[cur] > 0):
            ans = value[cur] * n - i;
            if (ans < m):
                return ans;
        cur = (cur * a) % m;
 
    return -1;
 
# Driver code
a = 2;
b = 3;
m = 5;
print(discreteLogarithm(a, b, m));
 
a = 3;
b = 7;
m = 11;
print(discreteLogarithm(a, b, m));
 
# This code is contributed by mits

C#

// C# program to calculate discrete logarithm
using System;
 
class GFG
{
     
static int discreteLogarithm(int a, int b, int m)
{
    int n = (int) (Math.Sqrt (m) + 1);
 
    // Calculate a ^ n
    int an = 1;
    for (int i = 0; i < n; ++i)
        an = (an * a) % m;
 
    int[] value = new int[m];
 
    // Store all values of a^(n*i) of LHS
    for (int i = 1, cur = an; i<= n; ++i)
    {
        if (value[ cur ] == 0)
            value[ cur ] = i;
        cur = (cur * an) % m;
    }
 
    for (int i = 0, cur = b; i<= n; ++i)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        if (value[cur] > 0)
        {
            int ans = value[cur] * n - i;
            if (ans < m)
                return ans;
        }
        cur = (cur * a) % m;
    }
    return -1;
}
 
// Driver code
static void Main()
{
    int a = 2, b = 3, m = 5;
    Console.WriteLine(discreteLogarithm(a, b, m));
 
    a = 3;
    b = 7;
    m = 11;
    Console.WriteLine(discreteLogarithm(a, b, m));
}
}
 
// This code is contributed by mits

PHP

<?php
// PHP program to calculate discrete logarithm
 
function discreteLogarithm($a, $b, $m)
{
    $n = (int)sqrt ($m) + 1;
 
    // Calculate a ^ n
    $an = 1;
    for ($i = 0; $i < $n; ++$i)
        $an = ($an * $a) % $m;
 
    $value = array_fill(0, $m, NULL);
 
    // Store all values of a^(n*i) of LHS
    for ($i = 1, $cur = $an; $i<= $n; ++$i)
    {
        if (! $value[ $cur ])
            $value[ $cur ] = $i;
        $cur = ($cur * $an) % $m;
    }
 
    for ($i = 0, $cur = $b; $i<= $n; ++$i)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        if ($value[$cur])
        {
            $ans = $value[$cur] * $n - $i;
            if ($ans < $m)
                return $ans;
        }
        $cur = ($cur * $a) % $m;
    }
    return -1;
}
 
// Driver code
$a = 2;
$b = 3;
$m = 5;
echo discreteLogarithm($a, $b, $m), "\n";
 
$a = 3;
$b = 7;
$m = 11;
echo discreteLogarithm($a, $b, $m);
 
// This code is contributed by ajit.
?>

Javascript

<script>
 
    // Javascript program to calculate
    // discrete logarithm
     
    function discreteLogarithm(a, b, m)
    {
        let n = parseInt(Math.sqrt(m), 10) + 1;
 
        // Calculate a ^ n
        let an = 1;
        for (let i = 0; i < n; ++i)
            an = (an * a) % m;
 
        let value = new Array(m);
        value.fill(0);
 
        // Store all values of a^(n*i) of LHS
        for (let i = 1, cur = an; i<= n; ++i)
        {
            if (value[ cur ] == 0)
                value[ cur ] = i;
            cur = (cur * an) % m;
        }
 
        for (let i = 0, cur = b; i<= n; ++i)
        {
            // Calculate (a ^ j) * b and check
            // for collision
            if (value[cur] > 0)
            {
                let ans = value[cur] * n - i;
                if (ans < m)
                    return ans;
            }
            cur = (cur * a) % m;
        }
        return -1;
    }
     
    let a = 2, b = 3, m = 5;
     
document.write(discreteLogarithm(a, b, m) + "</br>");
   
    a = 3;
    b = 7;
    m = 11;
     
document.write(discreteLogarithm(a, b, m));
 
</script>

Producción:  

3
-1

Complejidad temporal: O(sqrt(m)) 
Espacio auxiliar: O(sqrt(m))
Referencia:  
http://e-maxx-eng.appspot.com/algebra/discrete-log.html  
https://en.wikipedia .org/wiki/Baby-step_giant-step
Este artículo es una contribución de Shubham Bansal . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
 

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *