Longitud de la mediatriz de la recta que une los centros de dos circunferencias

Se dan dos círculos cuyos radios están dados, de modo que el más pequeño se encuentra completamente dentro del círculo más grande, y se tocan en un punto. Tenemos que encontrar la longitud de la mediatriz de la línea que une los centros de los círculos.
Ejemplos: 
 

Input: r1 = 5, r2 = 3
Output: 9.79796

Input: r1 = 8, r2 = 4
Output: 15.4919

Enfoque : 
 

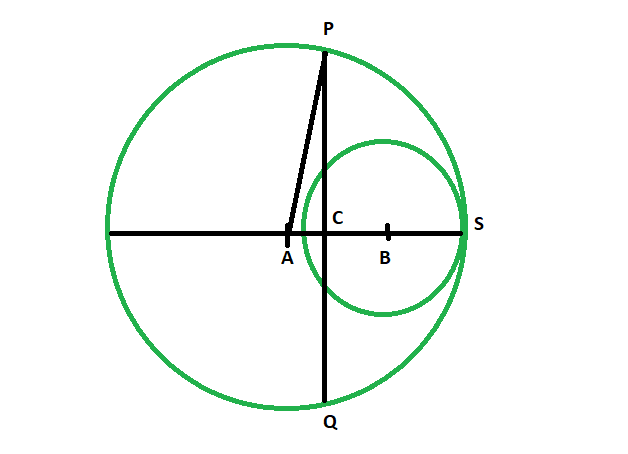
• Sean los dos círculos con centro en A y B . La bisectriz perpendicular PQ , biseca la recta en C . 
   
• Sea el radio del círculo más grande = r1 el 
  radio del círculo más pequeño = r2 
   
• entonces, AB = r1-r2 , 
   
• por lo tanto, CA = (r1-r2)/2 
   
• En la figura vemos 
  PA = r1 
   
• en el triángulo ACP , 
  PC^2 + AC^2 = PA^2 
  PC^2 = PA^2 – AC^2 
  PC^2 = r1^2 – (r1-r2)^2/4 
   
• entonces, PQ = 2*√(r1^2 – (r1-r2)^2/4) 
   

Longitud de la bisectriz perpendicular = 2 * sqrt(r1^2 – (r1-r2)*(r1-r2)/4)

A continuación se muestra la implementación del enfoque anterior: 
 

// C++ program to find the Length
// of the perpendicular bisector
// of the line joining the centers
// of two circles in which one lies
// completely inside touching the
// bigger circle at one point
 
#include <bits/stdc++.h>
using namespace std;
 
void lengperpbisect(double r1, double r2)
{
    double z = 2 * sqrt((r1 * r1)
                        - ((r1 - r2)
                           * (r1 - r2) / 4));
 
    cout << "The length of the "
         << "perpendicular bisector is "
         << z << endl;
}
 
// Driver code
int main()
{
    double r1 = 5, r2 = 3;
    lengperpbisect(r1, r2);
    return 0;
}

// Java program to find the Length
// of the perpendicular bisector
// of the line joining the centers
// of two circles in which one lies
// completely inside touching the
// bigger circle at one point
 
class GFG {
     
static void lengperpbisect(double r1, double r2)
{
    double z = 2 * Math.sqrt((r1 * r1)
                        - ((r1 - r2)
                        * (r1 - r2) / 4));
 
    System.out.println("The length of the "
        + "perpendicular bisector is "
        + z );
}
 
// Driver code
public static void main(String[] args)
{
    double r1 = 5, r2 = 3;
    lengperpbisect(r1, r2);
}
}
 
// This code has been contributed by 29AjayKumar

     
# Python program to find the Length
# of the perpendicular bisector
# of the line joining the centers
# of two circles in which one lies
# completely inside touching the
# bigger circle at one point
 
def lengperpbisect(r1, r2):
    z = 2 * (((r1 * r1) - ((r1 - r2) * (r1 - r2) / 4))**(1/2));
 
    print("The length of the perpendicular bisector is ", z);
 
 
# Driver code
r1 = 5; r2 = 3;
lengperpbisect(r1, r2);
 
# This code contributed by PrinciRaj1992

// C# program to find the Length
// of the perpendicular bisector
// of the line joining the centers
// of two circles in which one lies
// completely inside touching the
// bigger circle at one point
using System;
 
class GFG
{
     
static void lengperpbisect(double r1, double r2)
{
    double z = 2 * Math.Sqrt((r1 * r1)
                        - ((r1 - r2)
                        * (r1 - r2) / 4));
 
    Console.WriteLine("The length of the "
        + "perpendicular bisector is "
        + z );
}
 
// Driver code
public static void Main()
{
    double r1 = 5, r2 = 3;
    lengperpbisect(r1, r2);
}
}
 
// This code has been contributed by anuj_67..

<script>
// javascript program to find the Length
// of the perpendicular bisector
// of the line joining the centers
// of two circles in which one lies
// completely inside touching the
// bigger circle at one point
 
function lengperpbisect(r1 , r2)
{
    var z = 2 * Math.sqrt((r1 * r1)
                        - ((r1 - r2)
                        * (r1 - r2) / 4));
 
    document.write("The length of the "
        + "perpendicular bisector is "
        + z.toFixed(5) );
}
 
// Driver code
 
var r1 = 5, r2 = 3;
lengperpbisect(r1, r2);
 
 
// This code is contributed by 29AjayKumar
</script>

The length of the perpendicular bisector is 9.79796

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)