Longitud de la normal desde el origen en una línea recta cuyas intersecciones se dan

Dadas las intersecciones de una línea recta en ambos ejes como m y n . La tarea es encontrar la longitud de la normal en esta línea recta desde el origen.
Ejemplos: 
 

Entrada: m = 5, n = 3 
Salida: 2,57248
Entrada: m = 13, n = 9 
Salida: 7,39973 
 

Aproximación: Una normal a una línea es un segmento de línea dibujado desde un punto perpendicular a la línea dada. 
 

Sea p la longitud de la normal trazada desde el origen hasta una línea que subtiende un ángulo Θ con la dirección positiva del eje x de la siguiente manera. 
 

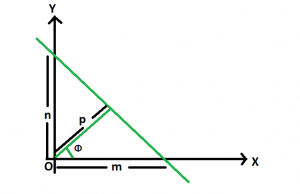
Entonces, tenemos cos Θ = p / m y sen Θ = p / n 
Ya que, sen ² Θ + cos ² Θ = 1 
Entonces, (p / m) ² + (p / n) ² = 1 
Obtenemos, p = m * n / √(m ² + n ² )
A continuación se muestra la implementación del enfoque anterior: 
 

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the normal
// of the straight line
float normal(float m, float n)
{
    // Length of the normal
    float N = (fabsf(m) * fabsf(n))
              / sqrt((fabsf(m) * fabsf(m))
                     + (fabsf(n) * fabsf(n)));
 
    return N;
}
 
// Driver code
int main()
{
    float m = -5, n = 3;
    cout << normal(m, n);
 
    return 0;
}

// Java implementation of the approach
class GFG
{
 
// Function to find the normal
// of the straight line
static float normal(float m, float n)
{
    // Length of the normal
    float N = (float) ((Math.abs(m) * Math.abs(n))
            / Math.sqrt((Math.abs(m) * Math.abs(m))
                    + (Math.abs(n) * Math.abs(n))));
 
    return N;
}
 
// Driver code
public static void main(String[] args)
{
    float m = -5, n = 3;
    System.out.println(normal(m, n));
}
}
 
// This code has been contributed by 29AjayKumar

# Python3 implementation of the approach
import math;
 
# Function to find the normal
# of the straight line
def normal(m, n):
 
    # Length of the normal
    N = ((abs(m) * abs(n)) /
        math.sqrt((abs(m) * abs(m)) +
                  (abs(n) * abs(n))));
 
    return N;
 
# Driver code
m = -5; n = 3;
print(normal(m, n));
 
# This code is contributed
# by Akanksha Rai

// C# implementation of the approach
using System;
 
class GFG
{
 
// Function to find the normal
// of the straight line
static float normal(float m, float n)
{
    // Length of the normal
    float N = (float)((Math.Abs(m) * Math.Abs(n)) /
                       Math.Sqrt((Math.Abs(m) * Math.Abs(m)) +
                                 (Math.Abs(n) * Math.Abs(n))));
 
    return N;
}
 
// Driver code
public static void Main()
{
    float m = -5, n = 3;
    Console.Write(normal(m, n));
}
}
 
// This code is contributed by Akanksha Rai

<?php
// PHP implementation of the approach
 
// Function to find the normal
// of the straight line
function normal($m, $n)
{
    // Length of the normal
    $N = (abs($m) * abs($n))  /
              sqrt((abs($m) * abs($m))  +
                   (abs($n) * abs($n)));
 
    return $N;
}
 
// Driver code
$m = -5; $n = 3;
echo normal($m, $n);
 
// This code is contributed by Ryuga
?>

<script>
 
// javascript implementation of the approach
 
 
// Function to find the normal
// of the straight line
function normal(m , n)
{
    // Length of the normal
    var N =  ((Math.abs(m) * Math.abs(n))
            / Math.sqrt((Math.abs(m) * Math.abs(m))
                    + (Math.abs(n) * Math.abs(n))));
 
    return N;
}
 
// Driver code
var m = -5, n = 3;
document.write(normal(m, n).toFixed(5));
 
// This code is contributed by Amit Katiyar
 
</script>

2.57248

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)