Longitud de la cuerda del círculo cuyo radio y el ángulo subtendido en el centro por la cuerda están dados

Dado un círculo cuyo radio y el ángulo subtendido en el centro por su cuerda están dados. La tarea es encontrar la longitud de la cuerda.
Ejemplos: 
 

Input: r = 4, x = 63 
Output: 4.17809

Input:: r = 9, x = 71
Output:: 10.448

Enfoque : 
 

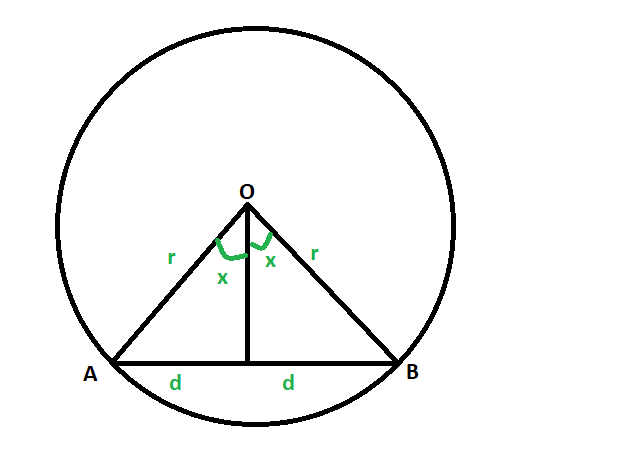
1. Sea el círculo con centro en O y radio r , y su cuerda sea AB .
2. la longitud de la cuerda sea 2d y el ángulo subtendido por ella en el centro sea 2x grados.
3. Como la perpendicular que cae en la cuerda biseca la cuerda, la perpendicular también divide por igual el ángulo subtendido 2x en x grados.
4. Entonces, del diagrama, 
   d/r = sin(x*π/180) (aquí x grados se convierte en radianes)
5. Entonces, d = rsin(x*π/180) 
   por lo tanto, 2d = 2rsin(x*π/180) 
    
6. Asi que, 

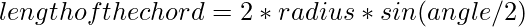
A continuación se muestra la implementación del enfoque anterior: 
 

// C++ program to find the length chord
// of the circle whose radius
// and the angle subtended at the centre
// is also given
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the length of the chord
void length_of_chord(double r, double x)
{
    cout << "The length of the chord"
         << " of the circle is "
         << 2 * r * sin(x * (3.14 / 180))
         << endl;
}
 
// Driver code
int main()
{
    double r = 4, x = 63;
    length_of_chord(r, x);
    return 0;
}

// Java program to find the length chord
// of the circle whose radius
// and the angle subtended at the centre
// is also given
 
class GFG
{
 
// Function to find the length of the chord
static void length_of_chord(double r, double x)
{
    System.out.println("The length of the chord"
        + " of the circle is "
        + 2 * r * Math.sin(x * (3.14 / 180)));
}
 
// Driver code
public static void main(String[] args)
{
    double r = 4, x = 63;
    length_of_chord(r, x);
}
}
 
// This code contributed by Rajput-Ji

# Python3 program to find the length chord
# of the circle whose radius
# and the angle subtended at the centre
# is also given
 
import math as mt
 
# Function to find the length of the chord
def length_of_chord(r, x):
 
    print("The length of the chord"
        ," of the circle is "
        ,2 * r * mt.sin(x * (3.14 / 180)))
 
 
# Driver code
r = 4
x = 63;
length_of_chord(r, x)
 
# This code is contributed by mohit kumar

// C# program to find the length chord
// of the circle whose radius
// and the angle subtended at the centre
// is also given
using System;
 
class GFG
{
     
    // Function to find the length of the chord
    static void length_of_chord(double r, double x)
    {
        Console.WriteLine("The length of the chord" +
                        " of the circle is " +
                        2 * r * Math.Sin(x * (3.14 / 180)));
                         
    }
 
    // Driver code
    public static void Main(String[] args)
    {
        double r = 4, x = 63;
        length_of_chord(r, x);
    }
}
 
// This code is Contributed by Naman_Garg

<?php
// PHP program to find the length chord
// of the circle whose radius and the
// angle subtended at the centre
// is also given
 
// Function to find the length of the chord
function length_of_chord($r, $x)
{
    echo "The length of the chord",
    " of the circle is "
    ,2 * $r * sin($x * (3.14 / 180)) ;
     
}
    // Driver code
    $r = 4; $x = 63;
    length_of_chord($r, $x);
 
    // This code is contributed by Ryuga
 
?>

<script>
 
// JavaScript program to find the length chord
// of the circle whose radius
// and the angle subtended at the centre
// is also given
 
 
// Function to find the length of the chord
function length_of_chord(r, x)
{
    document.write("The length of the chord"
        + " of the circle is "
        + 2 * r * Math.sin(x * (3.14 / 180))
        + "<br>");
}
 
// Driver code
 
    let r = 4, x = 63;
    length_of_chord(r, x);
 
// This code is contributed by Surbhi Tyagi.
 
</script>

The length of the chord of the circle is 7.12603

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)