Longitud de la tangente común directa entre los dos círculos que no se cortan

Dados dos círculos, de radios dados, tienen sus centros separados por una distancia dada, tal que los círculos no se tocan entre sí. La tarea es encontrar la longitud de la tangente común directa entre los círculos.
Ejemplos: 
 

Input: r1 = 4, r2 = 6, d = 12 
Output: 11.8322

Input: r1 = 5, r2 = 9, d = 25
Output: 24.6779

Enfoque : 
 

• Sean los radios de los círculos r1 y r2 respectivamente.
• Sea la distancia entre los centros d unidades.
• Dibuja una línea O paralela a PQ
• ángulo OPQ = 90 grados 
  ángulo O’QP = 90 grados 
  { la línea que une el centro del círculo con el punto de contacto forma un ángulo de 90 grados con la tangente }
• ángulo OPQ + ángulo O’QP = 180 grados 
  OP || código QR
• Dado que los lados opuestos son paralelos y los ángulos interiores son 90, entonces OPQR es un rectángulo.
• Entonces OP = QR = r1 y PQ = OR = d
• En el triángulo OO’R
  ángulo ORO’ = 90 
  Por el teorema de Pitágoras
  OR^2 + O’R^2 = (OO’^2) 
  OR^2 + (r1-r2)^2 = d^2
• entonces, O^2= d^2-(r1-r2)^2 
  O = √{d^2-(r1-r2)^2}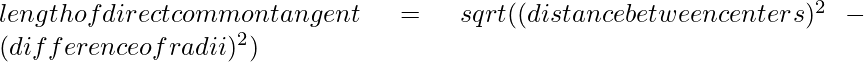 
  

A continuación se muestra la implementación del enfoque anterior:

// C++ program to find
// the length of the direct
// common tangent between two circles
// which donot touch each other
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the length of the direct common tangent
void lengtang(double r1, double r2, double d)
{
    cout << "The length of the direct"
        <<" common tangent is "
        << sqrt(pow(d, 2) - pow((r1 - r2), 2))
        << endl;
}
 
// Driver code
int main()
{
    double r1 = 4, r2 = 6, d = 12;
    lengtang(r1, r2, d);
    return 0;
}

// Java program to find
// the length of the direct
// common tangent between two circles
// which donot touch each other
class GFG
{
 
// Function to find the length of
// the direct common tangent
static void lengtang(double r1, double r2, double d)
{
    System.out.println("The length of the direct"
        +" common tangent is "
        +(Math.sqrt(Math.pow(d, 2) -
        Math.pow((r1 - r2), 2))));
}
 
// Driver code
public static void main(String[] args)
{
    double r1 = 4, r2 = 6, d = 12;
    lengtang(r1, r2, d);
}
}
 
/* This code contributed by PrinciRaj1992 */

# Python3 program to find
# the length of the direct
# common tangent between two circles
# which do not touch each other
import math
 
# Function to find the length
# of the direct common tangent
def lengtang(r1, r2, d):
    print("The length of the direct common tangent is",
        (((d ** 2) - ((r1 - r2) ** 2)) ** (1 / 2)));
 
# Driver code
r1 = 4; r2 = 6; d = 12;
lengtang(r1, r2, d);
 
# This code is contributed by 29AjayKumar

// C# program to find
// the length of the direct
// common tangent between two circles
// which donot touch each other
using System;
 
class GFG
{
 
    // Function to find the length of
    // the direct common tangent
    static void lengtang(double r1, double r2, double d)
    {
        Console.WriteLine("The length of the direct"
            +" common tangent is "
            +(Math.Sqrt(Math.Pow(d, 2) -
            Math.Pow((r1 - r2), 2))));
    }
     
    // Driver code
    public static void Main()
    {
        double r1 = 4, r2 = 6, d = 12;
        lengtang(r1, r2, d);
    }
}
 
// This code is contributed by AnkitRai01

<?php
// PHP program to find the length
// of the direct common tangent
// between two circles which
// donot touch each other
 
// Function to find the length
// of the direct common tangent
function lengtang($r1, $r2, $d)
{
    echo "The length of the direct",
            " common tangent is ",
        sqrt(pow($d, 2) -
            pow(($r1 - $r2), 2)), "\n";
}
 
// Driver code
$r1 = 4;
$r2 = 6;
$d = 12;
lengtang($r1, $r2, $d);
 
// This code is contributed by akt_mit
?>

<script>
 
// Javascript program to find
// the length of the direct
// common tangent between two circles
// which donot touch each other
 
 
// Function to find the length of the direct common tangent
function lengtang(r1, r2, d)
{
    document.write("The length of the direct common tangent is "+
        Math.sqrt(Math.pow(d, 2) - Math.pow((r1 - r2), 2)));
}
 
// Driver code
    var r1 = 4, r2 = 6, d = 12;
    lengtang(r1, r2, d);
 
</script>

Producción:

The length of the direct common tangent is 11.8322

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)