Aprendizaje automático para la detección de anomalías

La Detección de Anomalías es la técnica de identificación de eventos raros u observaciones que pueden generar sospechas por ser estadísticamente diferentes al resto de las observaciones. Tal comportamiento «anómalo» generalmente se traduce en algún tipo de problema como un fraude con tarjeta de crédito, una máquina defectuosa en un servidor, un ataque cibernético, etc.
Una anomalía se puede categorizar ampliamente en tres categorías:
 

1. Anomalía de punto: se dice que una tupla en un conjunto de datos es una anomalía de punto si está lejos del resto de los datos.
2. Anomalía contextual: una observación es una anomalía contextual si es una anomalía debido al contexto de la observación.
3. Anomalía colectiva: un conjunto de instancias de datos ayudan a encontrar una anomalía.

La detección de anomalías se puede realizar utilizando los conceptos de Machine Learning . Se puede hacer de las siguientes maneras:
 

1. Detección supervisada de anomalías: este método requiere un conjunto de datos etiquetados que contenga muestras normales y anómalas para construir un modelo predictivo para clasificar puntos de datos futuros. Los algoritmos más utilizados para este propósito son las redes neuronales supervisadas, el aprendizaje automático de vectores de soporte , el clasificador de vecinos más cercanos K , etc.
2. Detección de anomalías no supervisadas: este método requiere datos de entrenamiento y, en cambio, asume dos cosas sobre los datos, es decir, solo un pequeño porcentaje de datos es anómalo y cualquier anomalía es estadísticamente diferente de las muestras normales. Según las suposiciones anteriores, los datos se agrupan utilizando una medida de similitud y los puntos de datos que están lejos del grupo se consideran anomalías.

Ahora demostramos el proceso de detección de anomalías en un conjunto de datos sintéticos utilizando el algoritmo K-Nearest Neighbors que se incluye en el módulo pyod .
Paso 1: Importación de las bibliotecas requeridas
 

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import matplotlib.font_manager
from pyod.models.knn import KNN
from pyod.utils.data import generate_data, get_outliers_inliers

Paso 2: Crear los datos sintéticos
 

# generating a random dataset with two features
X_train, y_train = generate_data(n_train = 300, train_only = True,
                                                   n_features = 2)
 
# Setting the percentage of outliers
outlier_fraction = 0.1
 
# Storing the outliers and inliners in different numpy arrays
X_outliers, X_inliers = get_outliers_inliers(X_train, y_train)
n_inliers = len(X_inliers)
n_outliers = len(X_outliers)
 
# Separating the two features
f1 = X_train[:, [0]].reshape(-1, 1)
f2 = X_train[:, [1]].reshape(-1, 1)

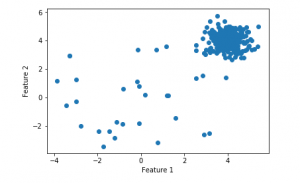
Paso 3: Visualización de los datos
 

# Visualising the dataset
# create a meshgrid
xx, yy = np.meshgrid(np.linspace(-10, 10, 200),
                     np.linspace(-10, 10, 200))
 
# scatter plot
plt.scatter(f1, f2)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')

Paso 4: Entrenamiento y evaluación del modelo
 

# Training the classifier
clf = KNN(contamination = outlier_fraction)
clf.fit(X_train, y_train)
 
# You can print this to see all the prediction scores
scores_pred = clf.decision_function(X_train)*-1
 
y_pred = clf.predict(X_train)
n_errors = (y_pred != y_train).sum()
# Counting the number of errors
 
print('The number of prediction errors are ' + str(n_errors))

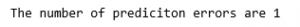
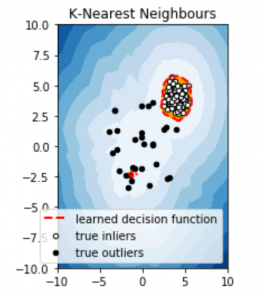
Paso 5: Visualización de las predicciones
 

# threshold value to consider a
# datapoint inlier or outlier
threshold = stats.scoreatpercentile(scores_pred, 100 * outlier_fraction)
 
# decision function calculates the raw
# anomaly score for every point
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]) * -1
Z = Z.reshape(xx.shape)
 
# fill blue colormap from minimum anomaly
# score to threshold value
subplot = plt.subplot(1, 2, 1)
subplot.contourf(xx, yy, Z, levels = np.linspace(Z.min(),
                  threshold, 10), cmap = plt.cm.Blues_r)
 
# draw red contour line where anomaly
# score is equal to threshold
a = subplot.contour(xx, yy, Z, levels =[threshold],
                     linewidths = 2, colors ='red')
 
# fill orange contour lines where range of anomaly
# score is from threshold to maximum anomaly score
subplot.contourf(xx, yy, Z, levels =[threshold, Z.max()], colors ='orange')
 
# scatter plot of inliers with white dots
b = subplot.scatter(X_train[:-n_outliers, 0], X_train[:-n_outliers, 1],
                                    c ='white', s = 20, edgecolor ='k')
 
# scatter plot of outliers with black dots
c = subplot.scatter(X_train[-n_outliers:, 0], X_train[-n_outliers:, 1],
                                    c ='black', s = 20, edgecolor ='k')
subplot.axis('tight')
 
subplot.legend(
    [a.collections[0], b, c],
    ['learned decision function', 'true inliers', 'true outliers'],
    prop = matplotlib.font_manager.FontProperties(size = 10),
    loc ='lower right')
 
subplot.set_title('K-Nearest Neighbours')
subplot.set_xlim((-10, 10))
subplot.set_ylim((-10, 10))
plt.show()

  
Referencia: https://www.analyticsvidhya.com/blog/2019/02/outlier-detection-python-pyod/