Matemáticas | LU Descomposición de un Sistema de Ecuaciones Lineales

La descomposición LU de una array es la factorización de una array cuadrada dada en dos arrays triangulares, una array triangular superior y una array triangular inferior, de modo que el producto de estas dos arrays da la array original. Fue presentado por Alan Turing en 1948, quien también creó la máquina de Turing.

Este método de factorizar una array como producto de dos arrays triangulares tiene varias aplicaciones, como la solución de un sistema de ecuaciones, que en sí mismo es una parte integral de muchas aplicaciones, como encontrar corriente en un circuito y solución de problemas de sistemas dinámicos discretos; encontrar la inversa de una array y encontrar el determinante de la array.
Básicamente, el método de descomposición LU es útil siempre que sea posible modelar el problema a resolver en forma de array. La conversión a la forma matricial y la resolución con arrays triangulares facilitan los cálculos en el proceso de encontrar la solución.

Una array cuadrada A se puede descomponer en dos arrays cuadradas L y U tales que A = LU donde U es una array triangular superior formada como resultado de aplicar el método de eliminación de Gauss en A, y L es una array triangular inferior con elementos diagonales siendo igual a 1

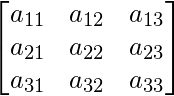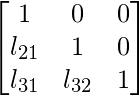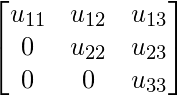Para A = $\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}$ , tenemos L = $\begin{bmatrix} 1 & 0 & 0 \\ l_{21} & 1 & 0 \\ l_{31} & l_{32} & 1 \end{bmatrix}$ y U = $\begin{bmatrix} u_{11} & u_{12} & u_{13} \\ 0 & u_{22} & u_{23} \\ 0 & 0 & u_{33} \end{bmatrix}$ ; tal que A = L U.

$\left[\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right]=\left[\begin{array}{lll} 1 & 0 & 0 \\ l_{21} & 1 & 0 \\ l_{31} & l_{32} & 0 \end{array}\right] *\left[\begin{array}{ccc} u_{11} & u_{12} & u_{13} \\ 0 & u_{22} & u_{23} \\ 0 & 0 & u_{33} \end{array}\right]$

Aquí se puede comparar y encontrar el valor de l ₂₁ , u ₁₁ , etc.

Método de Eliminación
de Gauss Según el método de Eliminación de Gauss:

Cualquier fila cero debe estar en la parte inferior de la array.
La primera entrada distinta de cero de cada fila debe estar en el lado derecho de la primera entrada distinta de cero de la fila anterior. Este método reduce la array a la forma escalonada de filas.

Pasos para la descomposición LU:

Dado un conjunto de ecuaciones lineales, primero conviértalas en forma matricial AX = C donde A es la array de coeficientes, X es la array variable y C es la array de números en el lado derecho de las ecuaciones.
Ahora, reduzca la array de coeficientes A, es decir, la array obtenida a partir de los coeficientes de las variables en todas las ecuaciones dadas, de modo que para ‘n’ variables tengamos una array nXn, a la forma escalonada de filas utilizando el método de eliminación de Gauss. La array así obtenida es U.
Para encontrar L, tenemos dos métodos. La primera es asumir los elementos restantes como algunas variables artificiales, hacer ecuaciones usando A = LU y resolverlas para encontrar esas variables artificiales.
El otro método es que los elementos restantes son los coeficientes multiplicadores por los cuales las posiciones respectivas se convirtieron en cero en la array U. (Este método es un poco difícil de entender con palabras, pero quedaría claro en el ejemplo a continuación)
Ahora, tenemos A (la array de coeficientes nXn), L (la array triangular inferior nXn), U (la array triangular superior nXn), X (la array de variables nX1) y C (la array de números nX1 a la derecha). lado de la mano de las ecuaciones).
El sistema de ecuaciones dado es AX = C. Sustituimos A = L U. Por lo tanto, tenemos LUX = C.
Ponemos Z = UX, donde Z es una array o variables artificiales y resolvemos para LZ = C primero y luego resolvemos para UX = Z para encontrar X o los valores de las variables, lo cual se requería.

Ejemplo:
Resuelva el siguiente sistema de ecuaciones utilizando el método de descomposición LU:

$\begin{equation*} x_1 + x_2 + x_3 = 1 \end{equation*} \begin{equation*} 4x_1 + 3x_2 - x_3 = 6 \end{equation*} \begin{equation*} 3x_1 + 5x_2 + 3x_3 = 4 \end{equation*}$

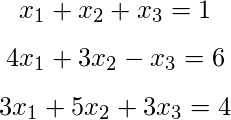
Solución: aquí tenemos

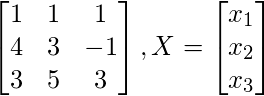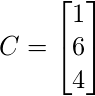A = $\begin{bmatrix} 1 & 1 & 1 \\ 4 & 3 & -1 \\ 3 & 5 & 3 \end{bmatrix} , X = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}$ y $C = \begin{bmatrix} 1 \\ 6 \\ 4 \end{bmatrix}$ tal que AX = C.

Ahora, primero lo consideramos 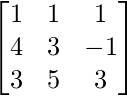$\begin{bmatrix} 1 & 1 & 1 \\ 4 & 3 & -1 \\ 3 & 5 & 3 \end{bmatrix}$ y lo convertimos en forma escalonada de filas usando el método de eliminación de Gauss.

Entonces, al hacer

$\begin{equation*} R_2 \to R_2 - 4R_1 \end{equation*}$

$\begin{equation*} R_3 \to R_3 - 3R_1 \end{equation*}$

obtenemos

$\begin{bmatrix} 1 & 1 & 1 \\ 4 & 3 & -1 \\ 3 & 5 & 3 \end{bmatrix} \sim$ $\begin{bmatrix} 1 & 1 & 1 \\ 0 & -1 & -5 \\ 0 & 2 & 0 \end{bmatrix}$

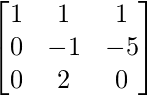
Ahora, al hacer

$\begin{equation*} R_3 \to R_3 - (-2)R_2 \end{equation*}$

obtenemos

$\sim \begin{bmatrix} 1 & 1 & 1 \\ 0 & -1 & -5 \\ 0 & 0 & -10 \end{bmatrix}$

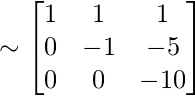
(Recuerde mantener siempre el signo ‘-‘ en el medio, reemplace el signo ‘+’ por dos signos ‘-‘)

Por lo tanto, obtenemos L = 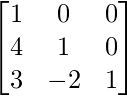$\begin{bmatrix} 1 & 0 & 0 \\ 4 & 1 & 0 \\ 3 & -2 & 1 \end{bmatrix}$ y U = $\begin{bmatrix} 1 & 1 & 1 \\ 0 & -1 & -5 \\ 0 & 0 & -10 \end{bmatrix}$

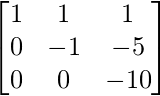
(nótese que en la array L, $l_{21} = 4$ es de (1), $l_{31} = 3$ es de (2) y $l_{32} = -2$ es de (3))

Ahora, asumimos Z $= \begin{bmatrix} z_1 \\ z_2 \\ z_3 \end{bmatrix}$ y resolvemos LZ = C.

$\begin{bmatrix} 1 & 0 & 0 \\ 4 & 1 & 0 \\ 3 & -2 & 1 \end{bmatrix} \begin{bmatrix} z_1 \\ z_2 \\ z_3 \end{bmatrix}$ $= \begin{bmatrix} 1 \\ 6 \\ 4 \end{bmatrix}$

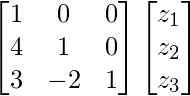
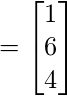
Entonces tenemos $z_1 = 1 ,$ $4z_1 + z_2 = 6 ,$ $3z_1 - 2z_2 + z_3 = 4 .$

Resolviendo, obtenemos $z_1 = 1$ , $z_2 = 2$ y $z_3 = 5$ .

Ahora, resolvemos UX = Z

$\begin{bmatrix} 1 & 1 & 1 \\ 0 & -1 & -5 \\ 0 & 0 & -10 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}$ $= \begin{bmatrix} 1 \\ 2 \\ 5 \end{bmatrix}$

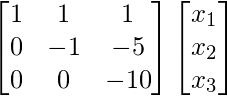
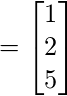
Por lo tanto, obtenemos $x_1 + x_2 + x_3 = 1 ,$ $-x_2 - 5x_3 = 2$ , $-10x_3 = 5 .$

Por lo tanto, la solución del sistema de ecuaciones lineales dado es $x_1 = 1$ , y $x_2 = 0.5$ , $x_3 = -0.5$ por lo tanto, la array X = $\begin{bmatrix} 1 \\ 0.5 \\ -0.5 \end{bmatrix}$

Ejercicio:
En la descomposición LU de la array

| 2  2 |
| 4  9 |

, si los elementos diagonales de U son ambos 1, entonces la entrada diagonal inferior l22 de L es (GATE CS 2015)
(A) 4
(B) 5
(C) 6
(D) 7
Para la solución, consulte https://www .geeksforgeeks.org/gate-gate-cs-2015-set-1-question-28/

Este artículo está compilado por Nishant Arora. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta