Matemáticas | Media, Varianza y Desviación Estándar

La media es el promedio de un conjunto dado de datos. Consideremos el siguiente ejemplo

$2,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9$

Estos ocho puntos de datos tienen la media (promedio) de 5:

$\frac{2 + 4 + 4 + 4 + 5 + 5 + 7 + 9}{8} = 5.$

$Formula : \mu=\frac{\sum_{i=1}^{N} x_{i}}{N}$

Donde μ es la media y x ₁ , x ₂ , x ₃ …., x _i son elementos. También tenga en cuenta que la media a veces se denota por $\bar{x}$

La varianza es la suma de los cuadrados de las diferencias entre todos los números y medias.
Desviación para el ejemplo anterior. Primero, calcule las desviaciones de cada punto de datos de la media y eleve al cuadrado el resultado de cada uno:

$\begin{array}{lll} (2-5)^2 = (-3)^2 = 9 && (5-5)^2 = 0^2 = 0 \\ (4-5)^2 = (-1)^2 = 1 && (5-5)^2 = 0^2 = 0 \\ (4-5)^2 = (-1)^2 = 1 && (7-5)^2 = 2^2 = 4 \\ (4-5)^2 = (-1)^2 = 1 && (9-5)^2 = 4^2 = 16. \\ \end{array}$

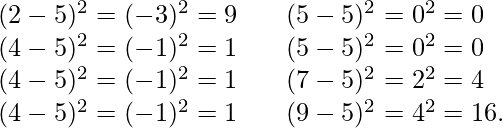
varianza =

$\frac{9 + 1 + 1 + 1 + 0 + 0 + 4 + 16}{8}$
= 4.
$Formula: \sigma^{2}= \frac { \sum_{i=1}^{N} (x_{i}-\mu)^{2}}{N}$

Donde μ es la media, N es el número total de elementos o la frecuencia de distribución.

La desviación estándar es la raíz cuadrada de la varianza. Es una medida de la medida en que los datos varían de la media.

Desviación estándar (para los datos anteriores) = $\sqrt{ 4 }$ = 2

¿Por qué los matemáticos eligieron un cuadrado y luego una raíz cuadrada para encontrar la desviación, por qué no simplemente tomaron la diferencia de valores?
Una razón es que la suma de las diferencias se convierte en 0 según la definición de media. La suma de diferencias absolutas podría ser una opción, pero con diferencias absolutas, era difícil probar muchos teoremas buenos. [Fuente: MIT Video Lecture en 1:19]

$\textup{Coefficient of variation } =\frac{ \textup{Standard deviation}}{Mean}*100$

El valor de la desviación estándar es 0 si todas las entradas en la entrada son iguales.
Si sumamos (o restamos) un número, digamos 7, a todos los valores en el conjunto de entrada, la media aumenta (o disminuye) en 7, pero la desviación estándar no cambia.
Si multiplicamos todos los valores en el conjunto de entrada por un número 7, tanto la media como la desviación estándar se multiplican por 7. Pero si multiplicamos todos los valores de entrada con un número negativo, digamos -7, la media se multiplica por -7, pero el la desviación estándar se multiplica por 7.
La desviación estándar y la varianza es una medida que indica cuán dispersos están los números. Mientras que la varianza te da una idea aproximada de la dispersión, la desviación estándar es más concreta y te da distancias exactas de la media.
La media, la mediana y la moda son la medida de tendencia central de los datos (ya sea agrupados o no agrupados).

Las siguientes preguntas se han realizado en los exámenes GATE del año anterior
https://www.geeksforgeeks.org/gate-gate-cs-2012-question-64/

Referencias:
https://en.wikipedia.org/wiki/Standard_deviation
http://staff.argyll.epsb.ca/jreed/math30p/statistics/standardDeviation.htm

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta