Matemáticas | Preguntas de práctica de teoría de grafos

Problema 1: hay 25 teléfonos en Geeksland. ¿Es posible conectarlos con cables para que cada teléfono esté conectado exactamente con otros 7? 

Solución: supongamos que tal arreglo es posible. Esto se puede ver como un gráfico en el que los teléfonos se representan usando vértices y los cables usando los bordes. Ahora tenemos 25 vértices en este gráfico. El grado de cada vértice en el gráfico es 7. Del lema del apretón de manos , lo sabemos.

sum of degrees of all vertices = 2*(number of edges)
number of edges = (sum of degrees of all vertices) / 2

Necesitamos entender que una arista conecta dos vértices. Entonces la suma de los grados de todos los vértices es igual al doble del número de aristas. Por lo tanto,

 25*7 = 2*(number of edges)
number of edges = 25*7 / 2 = 87.5

Esto no es un número entero. Como resultado, podemos concluir que nuestra suposición es incorrecta y que tal arreglo no es posible.   

Problema 2: la siguiente figura muestra una disposición de caballos en una cuadrícula de 3*3. 

 Figura: estado inicial ¿Es posible alcanzar el estado final como se muestra a continuación utilizando movimientos de caballo válidos? 

 Figura – estado final Solución – NO. Podrías pensar que necesitas ser un buen jugador de ajedrez para descifrar la pregunta anterior. Sin embargo, la pregunta anterior se puede resolver usando gráficos. Pero, ¿qué tipo de gráfico deberíamos dibujar? Deje que cada uno de los 9 vértices esté representado por un número como se muestra a continuación. 

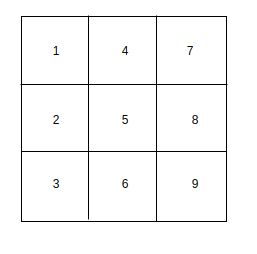
 Ahora consideramos cada cuadrado de la cuadrícula como un vértice en nuestro gráfico. Existe un borde entre dos vértices en nuestro gráfico si es posible un movimiento de caballo válido entre los cuadrados correspondientes en el gráfico. Por ejemplo, si consideramos el cuadrado 1. Los cuadrados alcanzables con movimientos de caballo válidos son 6 y 8. Podemos decir que el vértice 1 está conectado a los vértices 6 y 8 en nuestro gráfico. Del mismo modo, podemos dibujar el gráfico completo como se muestra a continuación. Claramente, el vértice 5 no se puede alcanzar desde ninguno de los cuadrados. Por lo tanto, ninguno de los bordes se conecta al vértice 5. 

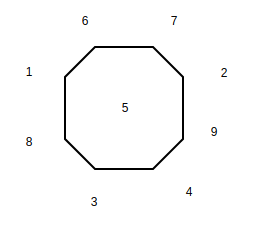
 Usamos un círculo hueco para representar un caballero blanco en nuestro gráfico y un círculo lleno para representar un caballero negro. Por lo tanto, el estado inicial del gráfico se puede representar como: 

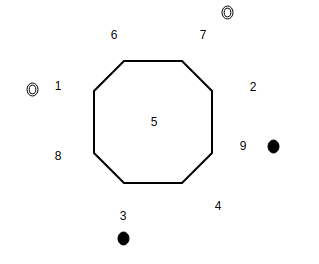
 Figura – estado inicial El estado final se representa como: 

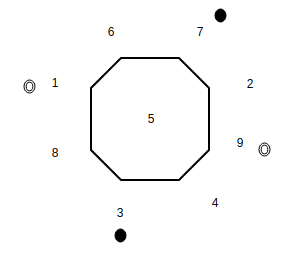
Figura – estado final Tenga en cuenta que para lograr el estado final es necesario que exista un camino en el que se crucen dos caballos (un caballo negro y un caballo blanco). Solo podemos mover los caballos en el sentido de las agujas del reloj o en el sentido contrario a las agujas del reloj en el gráfico (si dos vértices están conectados en el gráfico: significa que existe un movimiento de caballo correspondiente en la cuadrícula). Sin embargo, el orden en que aparecen los caballos en el gráfico no se puede cambiar. No hay forma posible de que un caballero cruce (dos caballeros no pueden existir en un vértice) el otro para lograr el estado final. Por lo tanto, podemos concluir que no importa cuál sea el arreglo final no es posible.  

 Problema 3: Hay 9 segmentos de línea dibujados en un plano. ¿Es posible que cada segmento de línea se cruce exactamente con otros 3? 

Solución: Este problema parece muy difícil inicialmente. Podríamos pensar en resolverlo usando gráficos. Pero, ¿cómo dibujamos el gráfico? Si tratamos de abordar este problema usando segmentos de línea como bordes de un gráfico, parece que no llegamos a ninguna parte (esto suena confuso al principio). Aquí necesitamos considerar un gráfico donde cada segmento de línea se representa como un vértice. Ahora dos vértices de este gráfico están conectados si los segmentos de línea correspondientes se cruzan. Ahora este gráfico tiene 9 vértices. El grado de cada vértice es 3. 

Sabemos que para un gráfico 

Suma de grados de todos los vértices = 2* Número de aristas en el gráfico 

Dado que la suma de los grados de los vértices en el problema anterior es 9*3 = 27, es decir, impar, tal arreglo no es posible. 

Este artículo es una contribución de Ankit Jain . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.