Hay una estructura jerárquica en una organización. Se va a organizar una fiesta. No pueden venir a la fiesta dos subordinados inmediatos. Un beneficio está asociado con cada persona. Tienes que maximizar el beneficio total de todas las personas que vienen a la fiesta.
Estructura jerárquica
En una organización jerárquica, todos los empleados (excepto el que está a la cabeza) son subordinados de algún otro empleado.
Los empleados solo reportan directamente a su superior inmediato. Esto permite una estructura flexible y eficiente.
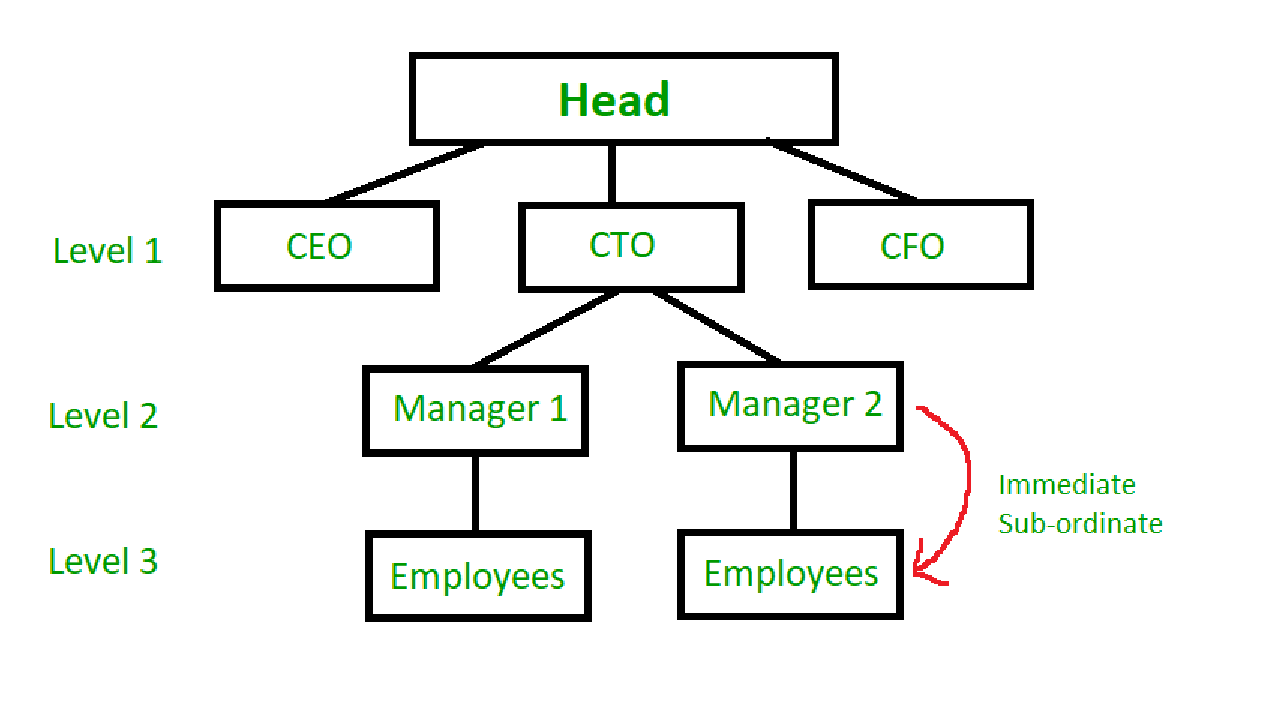
Para los propósitos de este problema, esta estructura puede imaginarse como un árbol, con cada empleado como su Node.
Ejemplos:
Input:
15
/ \
10 12
/ \ / \
26 4 7 9
Output: The Maximum Profit would be 15+12+26+9 = 62
The Parent 15 chooses sub-ordinate 12, 10 chooses 26 and 12 chooses 9.
Input:
12
/ | \
9 25 16
/ / \
13 13 9
Output: 12+25+13+13 = 63
Enfoque:
Dado el beneficio de cada empleado, tenemos que encontrar la suma máxima tal que no se inviten dos empleados (Nodes) con el mismo superior (Padre). Esto se puede lograr si cada empleado selecciona al subordinado con la máxima contribución para ir.
En el programa, la jerarquía de la empresa se implementa en forma de diccionario, siendo la clave una identificación de empleado única y los datos son una array de la forma [Beneficio asociado con este empleo, [Lista de subordinados inmediatos] ].
Para cada Empleado, el subordinado con la mayor ganancia asociada se suma a la ganancia total. Además, el Empleado a la cabeza siempre está invitado.
C++
// C++ program for above approach
#include <bits/stdc++.h>
using namespace std;
int getMaxProfit(vector<vector<int> > hier)
{
// The head has no competition and therefore invited
int totSum = hier[0][0];
for (vector<int> i : hier) {
vector<int> currentSuperior = i;
int selectedSub = 0;
// Select the subordinate with maximum
// value of each superior
for (int j = 1; j < currentSuperior.size(); j++) {
int e = currentSuperior[j];
if (hier[e - 1][0] > selectedSub) {
selectedSub = hier[e - 1][0];
}
}
totSum += selectedSub;
}
return totSum;
}
// Driver Code
int main()
{
// Define the Organization as a 2 - D array
// Index : [Profit, List of Employees]
/*
Same as example 1 given above
1:15
/ \
2:10 3:12
/ \ / \
4:26 5:4 6:7 7:9
*/
// Given input
vector<vector<int> > organization
= { { 15, 2, 3 }, { 10, 4, 5 }, { 12, 6, 7 },
{ 26 }, { 4 }, { 7 },
{ 9 } };
// Function call
int maxProfit = getMaxProfit(organization);
cout << maxProfit << "\n";
return 0;
}
Java
// Java program for above approach
class GFG {
static int getMaxProfit(int[][] hier)
{
// The head has no competition and therefore invited
int totSum = hier[0][0];
for (int i = 0; i < hier.length; i++) {
int selectedSub = 0;
for (int j = 1; j < hier[i].length; j++) {
int e = hier[i][j];
if (hier[e - 1][0] > selectedSub) {
selectedSub = hier[e - 1][0];
}
}
totSum += selectedSub;
}
return totSum;
}
public static void main(String[] args)
{
// Define the Organization as a 2 - D array
// Index : [Profit, List of Employees]
/*
Same as example 1 given above
1:15
/ \
2:10 3:12
/ \ / \
4:26 5:4 6:7 7:9
*/
// Given input
int[][] organization
= { { 15, 2, 3 }, { 10, 4, 5 }, { 12, 6, 7 },
{ 26 }, { 4 }, { 7 },
{ 9 } };
// Function call
int maxProfit = getMaxProfit(organization);
System.out.println(maxProfit);
}
}
// This code is contributed by rajsanghavi9.
Python3
# Python program for above approach
def getMaxProfit(hier):
# The head has no competition and therefore invited
totSum = hier[1][0]
for i in hier:
currentSuperior = hier[i]
selectedSub = 0
# select the subordinate with maximum
# value of each superior
for j in currentSuperior[1]:
if(hier[j][0] > selectedSub):
selectedSub = hier[j][0]
totSum += selectedSub
return totSum
# driver function
def main():
# Define the Organization as a Dictionary
# Index : [Profit, List of Employees]
# Same as example 1 given above
# 1:15
# / \
# 2:10 3:12
# / \ / \
# 4:26 5:4 6:7 7:9
organization = {1: [15, [2, 3]],
2: [10, [4, 5]], 3: [12, [6, 7]],
4: [26, []], 5: [4, []], 6: [7, []], 7: [9, []]}
maxProfit = getMaxProfit(organization)
print(maxProfit)
main()
62
Complejidad temporal: O(N)
Espacio auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por joshi_arihant y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA