Líneas distintas máximas que pasan por un solo punto

Dadas  las rectas representadas por dos puntos  y  . La tarea es encontrar el número máximo de líneas que pueden pasar por un solo punto, sin superponer (o cubrir) ninguna otra línea. Podemos mover cualquier línea pero no girarla.
Ejemplos: 
 

Input : Line 1 : x1 = 1, y1 = 1, x2 = 2, y2 = 2
        Line 2 : x2 = 2, y1 = 2, x2 = 4, y2 = 10
Output : 2
There are two lines. These two lines are not 
parallel, so both of them will pass through
a single point.


Input : Line 1 : x1 = 1, y1 = 5, x2 = 1, y2 = 10
        Line 2 : x2 = 5, y1 = 1, x2 = 10, y2 = 1
Output : 2

• Representa las líneas como un par 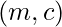 donde la línea se puede dar como  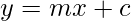, llamada forma de pendiente de línea. Ahora podemos ver que podemos cambiar la c por cualquier línea, pero no podemos modificar m .
• Líneas que tienen el mismo valor de m paralelas, dado que (c1 ≠ c2) . Además, dos rectas paralelas no pueden pasar por el mismo punto sin superponerse entre sí.
• Entonces, nuestro problema se reduce a encontrar diferentes valores de pendientes de un conjunto dado de líneas.

Podemos calcular la pendiente de una línea como  , agregarlos a un conjunto y contar el número de valores distintos de pendiente en el conjunto. Pero tenemos que manejar las líneas verticales por separado. 
Entonces, si  entonces, pendiente = INT_MAX . 
De lo contrario, pendiente =  .
A continuación se muestra la implementación del enfoque. 
 

// C++ program to find maximum number of lines
// which can pass through a single point
#include <bits/stdc++.h>
using namespace std;
 
// function to find maximum lines which passes
// through a single point
int maxLines(int n, int x1[], int y1[],
                int x2[], int y2[])
{
    unordered_set<double> s;
 
    double slope;
    for (int i = 0; i < n; ++i) {
        if (x1[i] == x2[i])
            slope = INT_MAX;
        else
            slope = (y2[i] - y1[i]) * 1.0
                    / (x2[i] - x1[i]) * 1.0;
 
        s.insert(slope);
    }
 
    return s.size();
}
 
// Driver program
int main()
{
    int n = 2, x1[] = { 1, 2 }, y1[] = { 1, 2 },
            x2[] = { 2, 4 }, y2[] = { 2, 10 };
    cout << maxLines(n, x1, y1, x2, y2);
    return 0;
}
// This code is written by
// Sanjit_Prasad

// Java program to find maximum number of lines
// which can pass through a single point
 
import java.util.*;
import java.lang.*;
import java.io.*;
 
class GFG{
 
// function to find maximum lines which passes
// through a single point
static int maxLines(int n, int x1[], int y1[],
                    int x2[], int y2[])
{
    Set<Double> s=new HashSet<Double>();
 
    double slope;
    for (int i = 0; i < n; ++i) {
        if (x1[i] == x2[i])
            slope = Integer.MAX_VALUE;
        else
            slope = (y2[i] - y1[i]) * 1.0
                    / (x2[i] - x1[i]) * 1.0;
 
        s.add(slope);
    }
 
    return s.size();
}
 
// Driver program
public static void main(String args[])
{
    int n = 2, x1[] = { 1, 2 }, y1[] = { 1, 2 },
            x2[] = { 2, 4 }, y2[] = { 2, 10 };
    System.out.print(maxLines(n, x1, y1, x2, y2));
}
}
// This code is written by
// Subhadeep

# Python3 program to find maximum number
# of lines which can pass through a
# single point
import sys
# function to find maximum lines
# which passes through a single point
def maxLines(n, x1, y1, x2, y2):
 
    s = [];
 
    slope=sys.maxsize;
    for i in range(n):
        if (x1[i] == x2[i]):
            slope = sys.maxsize;
        else:
            slope = (y2[i] - y1[i]) * 1.0 /(x2[i] - x1[i]) * 1.0;
 
        s.append(slope);
 
    return len(s);
 
# Driver Code
n = 2;
x1 = [ 1, 2 ];
y1 = [1, 2];
x2 = [2, 4];
y2 = [2, 10];
print(maxLines(n, x1, y1, x2, y2));
 
# This code is contributed by mits

// C# program to find maximum number of lines
// which can pass through a single point
using System;
using System.Collections.Generic;
 
class GFG
{
 
// function to find maximum lines which passes
// through a single point
static int maxLines(int n, int []x1, int []y1,
                    int []x2, int []y2)
{
    HashSet<Double> s = new HashSet<Double>();
 
    double slope;
    for (int i = 0; i < n; ++i)
    {
        if (x1[i] == x2[i])
            slope = int.MaxValue;
        else
            slope = (y2[i] - y1[i]) * 1.0
                    / (x2[i] - x1[i]) * 1.0;
 
        s.Add(slope);
    }
 
    return s.Count;
}
 
// Driver code
public static void Main()
{
    int n = 2;
    int []x1 = { 1, 2 }; int []y1 = { 1, 2 };
    int []x2 = { 2, 4 }; int []y2 = { 2, 10 };
    Console.Write(maxLines(n, x1, y1, x2, y2));
}
}
 
/* This code contributed by PrinciRaj1992 */

<?php
// PHP program to find maximum number
// of lines which can pass through a
// single point
 
// function to find maximum lines
// which passes through a single point
function maxLines($n, $x1, $y1, $x2, $y2)
{
    $s = array();
 
    $slope;
    for ($i = 0; $i < $n; ++$i)
    {
        if ($x1[$i] == $x2[$i])
            $slope = PHP_INT_MAX;
        else
            $slope = ($y2[$i] - $y1[$i]) * 1.0 /
                     ($x2[$i] - $x1[$i]) * 1.0;
 
        array_push($s, $slope);
    }
 
    return count($s);
}
 
// Driver Code
$n = 2;
$x1 = array( 1, 2 );
$y1 = array(1, 2);
$x2 = array(2, 4);
$y2 = array(2, 10);
echo maxLines($n, $x1, $y1, $x2, $y2);
 
// This code is contributed by mits
?>

<script>
     // JavaScript program to find maximum number
     // of lines which can pass through a
     // single point
     // function to find maximum lines
     // which passes through a single point
     function maxLines(n, x1, y1, x2, y2) {
       var s = [];
 
       //Max Integer Value
       var slope = 2147483647;
 
       for (let i = 0; i < n; i++) {
         if (x1[i] === x2[i]) slope = 2147483647;
         else slope = (((y2[i] - y1[i]) * 1.0) / (x2[i] - x1[i])) * 1.0;
 
         s.push(slope);
       }
       return s.length;
     }
     // Driver Code
     var n = 2;
     var x1 = [1, 2];
     var y1 = [1, 2];
     var x2 = [2, 4];
     var y2 = [2, 10];
     document.write(maxLines(n, x1, y1, x2, y2));
   </script>

2

Complejidad del tiempo: 

Complejidad espacial : O (N) ya que se usa espacio auxiliar para el conjunto