Medición de ángulos

En matemáticas, la palabra ‘trigonometría’ se obtiene de las dos palabras griegas ‘trigon’ y ‘metron’ que significa ‘medir los lados de un triángulo’. Entonces, las funciones trigonométricas expresan la relación entre un ángulo de un triángulo rectángulo y las razones de sus dos lados, las funciones trigonométricas también se conocen como funciones angulares. Generalmente, el seno, el coseno y la tangente se usan en las matemáticas modernas en comparación con la cosecante, la secante y la cotangente. Ahora, cada una de estas seis funciones trigonométricas tiene una función inversa correspondiente conocida como función trigonométrica inversa.

Hay una serie de ecuaciones trigonométricas e identidades que denotan la relación entre las funciones y ayudan a encontrar los ángulos. En este artículo, estudiaremos el concepto de triángulo, razones trigonométricas y funciones junto con varios ángulos y grados de medición.

Concepto básico de triángulo

Propiedades del Triángulo:

• Un triángulo tiene 3 lados, 3 vértices y 3 ángulos.
• La suma de todos los ángulos interiores de un triángulo es siempre igual a 180°, se conoce como propiedad de la suma de los ángulos de un triángulo.
• La diferencia entre la longitud de dos lados cualesquiera es siempre menor que el tercer lado.
• el area del triangulo es 1/2 x base x altura

Ángulos del triángulo:

• Un triángulo rectángulo: Tiene un ángulo recto. Un ángulo recto es un ángulo de tamaño 90°.
• Un triángulo obtuso: Tiene un ángulo obtuso. Un ángulo obtuso es un ángulo de tamaño superior a 90° pero inferior a 180°. 
• Triángulo acutángulo: Tiene ángulos agudos menores a 90° pero mayores a 0°.

Teorema de Pitágoras:

En un triángulo rectángulo, la suma de los cuadrados de los dos lados (aparte de la hipotenusa) de un triángulo rectángulo es igual al cuadrado del lado de la hipotenusa. O dicho de otro modo, la hipotenusa es el lado más largo de un triángulo rectángulo y es opuesto al ángulo de 90°. 

Fórmula:

hipotenusa ² = perpendicular ² + base ² 

O c ² = a ² + b ²

Donde a es el lado perpendicular, b es la base y c es el lado de la hipotenusa

Nota: el teorema de Pitágoras solo es aplicable a triángulos rectángulos.

Prueba del teorema de Pitágoras:

Dado: Un triángulo rectángulo ABC, cuyo ángulo recto está en B.

Para probar: AC ² = AB ² + BC ² 

Construcción: Construya una línea desde el ángulo B hasta la línea AC de modo que forme un ángulo de 90° con AC.

Prueba:

Como sabemos, △ADB ~ △ABC

Por tanto, AD/AB = AB/AC (lados correspondientes de triángulos semejantes)

O, AB ² = AD × AC ……………(1)

Además, △BDC ~△ABC

Por tanto, CD/BC = BC/AC (lados correspondientes de triángulos semejantes)

O, BC ² = CD × AC ……………(2)

Al sumar las ecuaciones (1) y (2) obtenemos,

AB ²  + BC ²  = AD × AC+ CD × AC

AB ²  + BC ²  = AC (AD + CD)

Ya que, AD + CD = AC

Entonces, CA ² = AB ²  + BC ²

Por lo tanto probado

razones trigonométricas

En trigonometría, existen 6 razones que se utilizan para encontrar los ángulos, se conocen como funciones trigonométricas. Y estas seis funciones trigonométricas son seno, coseno, secante, cosecante, tangente y cotangente.

Las funciones trigonométricas se extraen usando el teorema de Pitágoras y triángulos rectángulos. Las razones trigonométricas son:

sen θ = P/H

cos θ = B/H

tan θ = P/B = sen θ/cos θ

cot θ = 1/tan θ = cos θ/sen θ = B/P

cosec θ = 1/sen θ = H/P

seg θ = 1/cos θ = H/B

Tabla trigonométrica: La tabla trigonométrica es básicamente una colección sistemática de valores de funciones trigonométricas (sen, cos, tan, cot, sec y cosec) en ángulos estándar que incluyen 0°, 30°, 45°, 60°, 90°. Sin embargo, también se pueden encontrar otros ángulos usando esta tabla.

θ	0°	30°	45°	60°	90°
sen θ	0	1/2	1/√2	√3/2	1
cos θ	1	√3/2	1/√2	1/2	0
bronceado θ	0	1/√3	1	√3	no definida
cuna	no definida	√3	1	1/√3	0
segundo θ	1	2/√3	√2	2	no definida
cosec θ	no definida	2	√2	2/√3	1

Identidades trigonométricas:

• Identidades pitagóricas: 

La identidad de Pitágoras son aquellas identidades que se utilizan para mostrar el teorema de Pitágoras en términos de funciones trigonométricas.

sen ² θ + cos ² θ = 1

1 + tan ² θ = sen ² θ

1 + cuna ² θ = cosec ² θ

• Identidades recíprocas

cosec θ = 1/sen θ

seg θ = 1/cos θ

cuna θ = 1/bronceado θ

sen θ = 1/coseg θ

cos θ = 1/seg θ

tan θ = 1/cuna θ

• Identidades co-funcionales:

Las identidades de cofunción indican la relación entre sen, cos, tan, cot, sec y cosec. El valor de una función trigonométrica de un ángulo es igual al valor de la cofunción del complemento. Debes recordar esto ‘que un complemento se define como dos ángulos cuya suma es 90°’.

sin(90 − θ) = cos θ

cos(90 − θ) = sen θ

tan(90 − θ) = cuna θ

cuna(90 − θ) = tan θ

segundo(90 − θ) = cosegundo θ

cosec(90 − θ) = sec θ​
 

• Identidades de suma y diferencia:

sen(x + y) = senx acogedor + cosx senoidal

cos(x + y) = cosx acogedor – senx senoidal

tan(x + y) = 

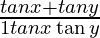
sen(x – y) = senx acogedor – cosx senoidal

cos (x – y) = cosx acogedor + senx senoidal

bronceado (x − y) = 

cuna (x + y) =

cuna (x – y) = 

• Identidades de doble ángulo:

 Doble, significa cuando el tamaño del ángulo es el doble del anterior.

sen(2x) = 2 senx cosx = 

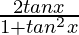
cos(2x) = cos ² x – sen ² x = 

cos(2x) = 2 cos ² x − 1 = 1 – 2 sen ² x

tan(2x) = 

segundo (2x) = 

• Identidades de triple ángulo:

sen 3x = 3 senx – 4 sen ³ x

cos 3x = 4 cos ³ x-3 cos x

bronceado 3x = 

• Suma de identidades de productos:

sen x + sen = 

sen x – sen = 

cosx + acogedor = 

cosx – acogedor = 

Medición de ángulo

El ángulo es una medida de la rotación de un rayo dado desde su punto inicial. El rayo original se conoce como el lado inicial del ángulo y la posición final del rayo después de la rotación se conoce como el lado terminal. El punto de rotación se conoce como vértice. Si la dirección de rotación es en sentido contrario a las manecillas del reloj, entonces se dice que el ángulo es ‘+’ y si la dirección de rotación es en el sentido de las manecillas del reloj, entonces el ángulo es ‘-‘. En trigonometría, el valor del ángulo oscila entre 0 y 360.

Hay dos unidades de medida para los ángulos, a saber:

1. grados
2. radianes

Medida de grado:

En general, podemos medir un ángulo determinando la cantidad de rotación que toma desde el lado inicial hasta el lado terminal. Entonces, podemos medir un ángulo usando grados. Una medida de un grado (1°) equivale a una rotación de 1/360 de una revolución completa. Aquí, una revolución se usa para medir un ángulo que se crea cuando el lado inicial gira alrededor de su vértice hasta que alcanza nuevamente su posición inicial.

Cuando medimos un ángulo, es conveniente marcar grados en la circunferencia de un círculo. Por lo tanto, en una revolución completa, el ángulo es de 360°, en media revolución, el ángulo es de 180°, en un cuarto de revolución, el ángulo es de 90°, y así sucesivamente.

un ángulo completo = 360 °

un grado = rotación de (1/360) ^de una revolución completa

1° = 60 minutos  

1° = 60′

1 minuto = 60 segundos  

1′ = 60”

Medida en radianes: 

También podemos medir un ángulo usando radianes. Una medida en radianes es la relación entre la longitud de un arco circular y el radio del arco. Dado que el radián es la relación de una longitud a la longitud, el resultado es un número puro que no necesita ningún símbolo de unidad.

1 radián = 1 ^c 

1 radián = Ángulo subtendido por un arco de unidad de longitud en el punto central del círculo.

1 unidad de longitud de arco = 1 radian

2 unidades de longitud de arco = 2 radianes

2π unidad de longitud de arco (revolución completa) = 2π radianes

1 revolución completa = 360° = 2π ^c

360° = 2π radianes

En un círculo, si el radio del círculo es r, una longitud de arco l subtiende un ángulo θ en el centro, entonces θ (en radianes) = l/r o l = rθ. Donde l = longitud del arco y, r = radio del círculo.

Relación entre grados y radianes:

Como sabemos que un círculo subtiende en su centro un ángulo cuya medida es 2π radianes y 360°.

Entonces, 2π radianes = 360°

π radianes = 180°

Como sabemos que π = 22/7

entonces 1 radián = 180°/π = 57°16′(aprox.)

también, 1° = π /180 = 0.0174 (aprox.)

Fórmula:

Ángulo en Radianes = Ángulo en Grados x π/180

o

Ángulo en Grados = Ángulo en Radianes x π/180

La siguiente tabla muestra la relación entre grado, radianes y revolución:

la licenciatura	radián	revolución
0°	0	0
30°	π/6	1/12
45°	π/4	1/8
60°	π/3	1/6
90°	π/2	1/4
120°	2π/3	1/3
180°	π	1/2
360°	2π	1

 

Problemas de muestra

Pregunta 1. Convierte 90 grados a radianes.

Solución: 

Dado, 90° es decir el ángulo

Como sabemos que,

Ángulo en radianes = Ángulo en grado x (π/180)

= 90 x (π/180)

= π/2

Por lo tanto, 90° es igual a π/2 en radianes.

Pregunta 2. Convierta π/6 en grados.

Solución: 

Usando la fórmula anterior

obtenemos, π/6 × (180/π) 

= 180/6 

= 30°

Pregunta 3. Convierte 15 grados a radianes.

Solución: 

Usando la fórmula anterior,

obtenemos, 15 x π/180

= π/12

Pregunta 4. Si cos x = -4/5 y x está en el tercer cuadrante, encuentre el valor de sen x, tan x. 

Solución: 

Dado que cos x = -4/5 y se encuentra en el tercer cuadrante

Entonces, usando la identidad sen ² θ + cos ² θ = 1, obtenemos

 sen ² θ = 1 – cos ² θ

 sen ² x = 1 – (-4/5) ²

= 1 – (16/25)

= (25 – 16)/25

= 9/25

sen x= ±3/5

Se da que x está en el tercer cuadrante
Entonces, sen x= -3/5

Ahora encontramos tan x 

Como sabemos que tan x = sen x/cos x

Tan x = -3/5 /-4/5 = 3/4

Pregunta 5. Encuentra el valor de sen 21 π/2

Solución: 

De acuerdo a la pregunta tenemos que encontrar el valor de sen 21 π/2

sen 21π/2 = sen(10π + π/2) = sen π/2 = 1

Pregunta 6. Un triángulo rectángulo ABC, rectángulo en B, hipotenusa AC = 10 cm, base BC = 2 cm y perpendicular AB = 5 cm y si ∠ACB = θ, entonces encuentra el valor de todas las razones trigonométricas.

Solución: 

Dado que en el triángulo ABC

Hipotenusa AC = 10 cm 

Base BC = 2 cm

AB perpendiculares = 5 cm

Como sabemos que 

sen θ = P/H = 5/10 = 1/2

cos θ = B/H = 2/10 = 1/5

tan θ = P/B = 5/2

cuna θ = B/P = 2/5

cosec θ = H/P = 10/5 = 2

segundo θ = H/B = 10/2 = 5

Pregunta 7. Encuentra el valor de cot θ si sen θ = 10 y cos θ = 5.

Solución:

Dado que sen θ = 10 y cos θ = 5

Tenemos que encontrar cot θ 

Como sabemos que cot θ = cosθ/sinθ 

cuna θ = 5/10

cuna θ = 1/5

Pregunta 8. Encuentra el valor de cosec θ si sen θ = 10.

Solución:

Dado que sen θ = 10 

Tenemos que encontrar cosec θ 

Como sabemos que cosec θ = 1/sinθ 

Entonces, cosec θ = 1/10 

Pregunta 9. Un triángulo rectángulo ABC, rectángulo en B, hipotenusa AC = 20 cm, base BC = 5 cm y perpendicular AB = 10 cm y si ∠ACB = θ, entonces encuentra el valor de tanθ y cos θ.

Solución:

Dado que en el triángulo ABC

Hipotenusa AC = 20 cm 

BC base = 5 cm

AB perpendicular = 10 cm

Como sabemos que 

sen θ = P/H = 10/20 = 1/2

cos θ = B/H = 5/20 = 1/4

tan θ = P/B = 10/5 = 2

Pregunta 10. Encuentra el valor de tan θ si sen θ = 30 y cos θ = 5.

Solución:

Dado que sen θ = 30 y cos θ = 5

Tenemos que encontrar tan θ 

Como sabemos que tan θ = sinθ /cosθ

tan θ = 30/5 = 6